浅谈图神经网络模型

1.前言

发展历史：

最早的GNN主要解决的还是如分子结构分类等严格意义上的图论问题。但实际上欧式空间(比如像图像 Image)或者是序列(比如像文本 Text)，许多常见场景也都可以转换成图(Graph)，然后就能使用图神经网络技术来建模。

直到2013年，在图信号处理(Graph Signal Processing)的基础上，Bruna(这位是LeCun的学生)在文献 [3]中首次提出图上的基于频域(Spectral-domain)和基于空域(Spatial-domain)的卷积神经网络。

图神经网络与图表示学习(Represent Learning for Graph)的发展历程也惊人地相似。2014年，在word2vec 的启发下，Perozzi等人提出了DeepWalk ，开启了深度学习时代图表示学习的大门。
更有趣的是，就在几乎一样的时间，Bordes等人提出了大名鼎鼎的TransE ，为知识图谱的分布式表示(Represent Learning for Knowledge Graph)奠定了基础。

2.GNN

图论中的图(Graph)。它是一种由若干个结点(Node)及连接两个结点的边(Edge)所构成的图形，用于刻画不同结点之间的关系。

状态更新与输出

它的理论基础是不动点理论。给定一张图 $G$，每个结点都有其自己的特征(feature), 本文中用${\mathbf{x}}_v$表示结点v的特征；连接两个结点的边也有自己的特征，本文中用${\mathbf{x}}_{(v,u)}$表示结点v与结点u之间边的特征；GNN的学习目标是获得每个结点的图感知的隐藏状态 ${\mathbf{h}}_v$(state embedding)，这就意味着：对于每个节点，它的隐藏状态包含了来自邻居节点的信息。
那么，如何让每个结点都感知到图上其他的结点呢？GNN通过迭代式更新所有结点的隐藏状态来实现，在$t+1$时刻，结点$v$的隐藏状态按照如下方式更新：

$${\mathbf{h}}_v^{t+1}=f\left({\mathbf{x}}_v,{\mathbf{x}}_{c}o[v],{\mathbf{h}}_n^{t}e[v],{\mathbf{x}}_{n}e[v]\right)$$

上面这个公式中的 $f$ 就是隐藏状态的状态更新函数，在论文中也被称为局部转移函数(local transaction function)。
公式中的${\mathbf{x}}_{c}o[v]$指的是与结点$v$相邻的边的特征，${\mathbf{x}}_{n}e[v]$指的是结点$v$的邻居结点的特征，${\mathbf{h}}_n^{t}e[v]$则指邻居结点在$t$时刻的隐藏状态。

利用神经网络(Neural Network)来拟合这个复杂函数 $f$。值得一提的是，虽然看起来 $f$ 的输入是不定长参数，但在 $f$ 内部我们可以先将不定长的参数通过一定操作变成一个固定的参数。

举例：

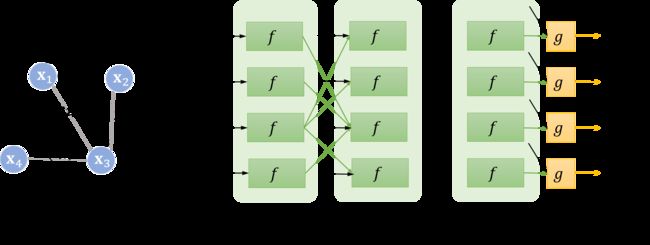
假设结点$5$为中心结点，不断地利用当前时刻邻居结点的隐藏状态作为部分输入来生成下一时刻中心结点的隐藏状态，直到每个结点的隐藏状态变化幅度很小，整个图的信息流动趋于平稳。至此，每个结点都“知晓”了其邻居的信息。状态更新公式仅描述了如何获取每个结点的隐藏状态，除它以外，我们还需要另外一个函数 $g$ 来描述如何适应下游任务。举个例子，给定一个社交网络，一个可能的下游任务是判断各个结点是否为水军账号。

在原论文中，$g$ 又被称为局部输出函数(local output function)，与 $f$ 类似，$g$ 也可以由一个神经网络来表达，它也是一个全局共享的函数。那么，整个流程可以用下面这张图表达：

对于不同的图来说，收敛的时刻可能不同，因为收敛是通过两个时刻$p$-范数的差值是否小于某个阈值 $ϵ$来判定的，比如：

$$||{\mathbf{H}}^{t+1}|{|}_2-||{\mathbf{H}}^t|{|}_2<ϵ$$

不动点理论
GNN的理论基础是不动点(the fixed point)理论，这里的不动点理论专指巴拿赫不动点定理(Banach’s Fixed Point Theorem)。首先我们用 $F$ 表示若干个 $f$ 堆叠得到的一个函数，也称为全局更新函数，那么图上所有结点的状态更新公式可以写成：
$${\mathbf{H}}^{t+1}=F\left({\mathbf{H}}^t,\mathbf{X}\right)$$

不动点定理指的就是，不论${\mathbf{H}}^0$是什么，只要 $F$ 是个压缩映射(contraction map)，${\mathbf{H}}^0$经过不断迭代都会收敛到某一个固定的点，我们称之为不动点。那压缩映射又是什么呢，一张图可以解释得明明白白：

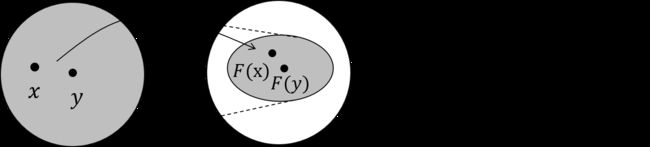
也就是说，经过 $F$ 变换后的新空间一定比原先的空间要小，原先的空间被压缩了。想象这种压缩的过程不断进行，最终就会把原空间中的所有点映射到一个点上。

f 具体实现

在具体实现中， $f$ 其实通过一个简单的前馈神经网络(Feed-forward Neural Network)即可实现。比如说，一种实现方法可以是把每个邻居结点的特征、隐藏状态、每条相连边的特征以及结点本身的特征简单拼接在一起，在经过前馈神经网络后做一次简单的加和。

$$\begin{array}{l}{\mathbf{h}}_v^{t+1}=f\left({\mathbf{x}}_v,{\mathbf{x}}_{c}o[v],{\mathbf{h}}_n^{t}e[v],{\mathbf{x}}_{n}e[v]\right)\\ ={\sum }_{u\in ne[v]}FNN\left(\left[{\mathbf{x}}_v;{\mathbf{x}}_{(u,v)};{\mathbf{h}}_u^t;{\mathbf{x}}_u\right]\right)\end{array}$$

那我们如何保证 $f$ 是个压缩映射呢，其实是通过限制 $f$ 对 $\mathbf{H}$ 的偏导数矩阵的大小，这是通过一个对雅可比矩阵(Jacobian Matrix)的惩罚项(Penalty)来实现的。
在代数中，有一个定理是: $f$ 为压缩映射的等价条件是 $f$ 的梯度/导数要小于1。这个等价定理可以从压缩映射的形式化定义导出，我们这里使用 $||x||$ 表示 $x$ 在空间中的范数(norm)。范数是一个标量，它是向量的长度或者模，$||x||$ 是 $x$ 在有限空间中坐标的连续函数。这里把 $x$ 简化成1维的，坐标之间的差值可以看作向量在空间中的距离，根据压缩映射的定义，可以导出：

$$||F(x)-F(y)||\le c||x-y||,0\le c<1$$
$$\frac{||F(x)-F(y)||}{||x-y||}\le c$$
$$\frac{||F(x)-F(x-\Delta x)||}{||\Delta x||}\le c$$
$$||F^{\prime }(x)||=||\frac{\partial F(x)}{\partial x}||\le c$$

推广一下，即得到雅可比矩阵的罚项需要满足其范数小于等于$c$等价于压缩映射的条件。根据拉格朗日乘子法，将有约束问题变成带罚项的无约束优化问题，训练的目标可表示成如下形式：

$$J=Loss+\lambda \cdot \max (\frac{||\partial FNN||}{||\partial \mathbf{h}||}-c,0),c\in (0,1)$$

其中$\lambda$是超参数，与其相乘的项即为雅可比矩阵的罚项。

损失函数定义及模型学习
模型的损失即通过这些有监督信号的结点得到。假设监督结点一共有 $p$ 个，模型损失可以形式化为：

$$Loss=\sum _{i=1}^p\left({\mathbf{t}}_i-{\mathbf{o}}_i\right)$$

那么，模型如何学习呢？根据前向传播计算损失的过程，不难推出反向传播计算梯度的过程。在前向传播中，模型：

1. 调用 $f$ 若干次，比如 $T_n$次，直到 ${\mathbf{h}}_v^{T_n}$ 收敛。
2. 此时每个结点的隐藏状态接近不动点的解。
3. 对于有监督信号的结点，将其隐藏状态通过 $g$ 得到输出，进而算出模型的损失。

根据上面的过程，在反向传播时，我们可以直接求出 $f$ 和 $g$ 对最终的隐藏状态 ${\mathbf{h}}_v^{T_n}$ 的梯度。然而，因为模型递归调用了 $f$ 若干次，为计算 $f$ 和 $g$ 对最初的隐藏状态 ${\mathbf{h}}_v^0$ 的梯度，我们需要同样递归式/迭代式地计算 $T_n$ 次梯度。最终得到的梯度即为 $f$ 和 $g$ 对 ${\mathbf{h}}_v^0$ 的梯度，然后该梯度用于更新模型的参数。这个算法就是 Almeida-Pineda 算法[9]。

3.GNN特点

GNN与RNN区别：

• GNN的基础理论是不动点理论，这就意味着GNN沿时间展开的长度是动态的，是根据收敛条件确定的，而RNN沿时间展开的长度就等于序列本身的长度。
• GNN每次时间步的输入都是所有结点 $v$ 的特征，而RNN每次时间步的输入是该时刻对应的输入。同时，时间步之间的信息流也不相同，前者由边决定，后者则由序列的读入顺序决定。
• GNN采用 AP 算法反向传播优化，而RNN使用BPTT(Back Propogation Through Time)优化。前者对收敛性有要求，而后者对收敛性是没有要求的。
• GNN循环调用 $f$ 的目标是得到每个结点稳定的隐藏状态，所以只有在隐藏状态收敛后才能输出；而RNN的每个时间步上都可以输出，比如语言模型。

4. 门控图神经网络(Gated Graph Neural Network)

门控图神经网络**(Gated Graph Neural Network, GGNN) [10]就出现了。虽然在这里它们看起来类似，但实际上，它们的区别非常大，其中最核心的不同即是门控神经网络不以不动点理论为基础。这意味着：$f$ 不再需要是一个压缩映射；迭代不需要到收敛才能输出，可以迭代固定步长；优化算法也从 AP 算法转向 BPTT。

状态更新

与图神经网络定义的范式一致，GGNN也有两个过程：状态更新与输出。相比GNN而言，它主要的区别来源于状态更新阶段。具体地，GGNN参考了GRU的设计，把邻居结点的信息视作输入，结点本身的状态视作隐藏状态，其状态更新函数如下:

$${\mathbf{h}}_v^{t+1}=\mathrm{GRU}\left({\mathbf{h}}_v^t,\sum _{u\in ne[v]}{\mathbf{W}}_{edge}{\mathbf{h}}_u^t\right)$$

如果读者对GRU的更新公式熟悉的话，对上式应该很好理解。仔细观察上面这个公式，除了GRU式的设计外，GGNN还针对不同类型的边引入了可学习的参数$\mathbf{W}$。每一种 $edge$ 对应一个 ${\mathbf{W}}_{edge}$，这样它就可以处理异构图。

在GNN里需要作为输入的结点特征 ${\mathbf{x}}_v$ 没有出现在GGNN的公式中! 但实际上，这些结点特征对我们的预测至关重要，因为它才是各个结点的根本所在。

为了处理这个问题，GGNN将结点特征作为隐藏状态初始化的一部分。那么重新回顾一下GGNN的流程，其实就是这样：

• 用结点特征初始化各个结点的(部分)隐藏状态。
• 对整张图，按照上述状态更新公式固定迭代若干步。
• 对部分有监督信号的结点求得模型损失，利用BPTT算法反向传播求得${\mathbf{W}}_{edge}$和GRU参数的梯度。

5. 图卷积神经网络

• 图里的邻居结点不固定，所以传统的卷积核不能直接用于抽取图上结点的特征。

真正的难点聚焦于邻居结点数量不固定上。那么，研究者如何解决这个问题呢？其实说来也很简单，目前主流的研究从2条路来解决这件事：

• 提出一种方式把非欧空间的图转换成欧式空间。
• 找出一种可处理变长邻居结点的卷积核在图上抽取特征。

这两条实际上也是后续图卷积神经网络的设计原则，图卷积的本质是想找到适用于图的可学习卷积核。

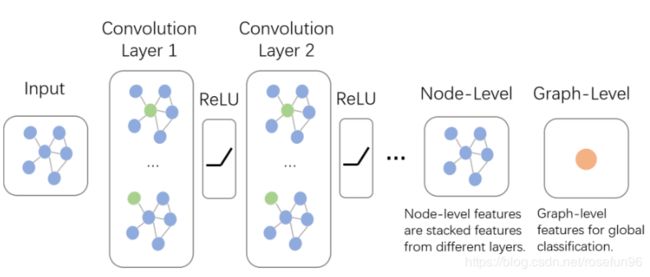
卷积操作关心每个结点的隐藏状态如何更新，而对于Graph-Level的任务，它们会在卷积层后加入更多操作。

空域卷积(Spatial Convolution)

从设计理念上看，空域卷积与深度学习中的卷积的应用方式类似，其核心在于聚合邻居结点的信息。比如说，一种最简单的无参卷积方式可以是：将所有直连邻居结点的隐藏状态加和，来更新当前结点的隐藏状态。

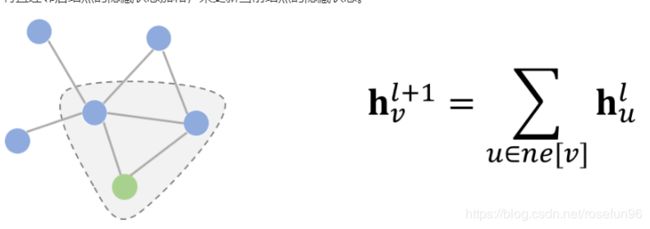
这里非参式的卷积只是为了举一个简单易懂的例子，实际上图卷积在建模时需要的都是带参数、可学习的卷积核。

消息传递网络(Message Passing Neural Network)

严格意义上讲，MPNN不是一种具体的模型，而是一种空域卷积的形式化框架。

它将空域卷积分解为两个过程：消息传递与状态更新操作，分别由$M_l(\cdot )$和$U_l(\cdot )$函数完成。将结点$v$的特征${\mathbf{x}}_v$作为其隐藏状态的初始态${\mathbf{h}}_v^0$后，空域卷积对隐藏状态的更新由如下公式表示：

$${\mathbf{h}}_v^{l+1}=U_{l+1}\left({\mathbf{h}}_v,\sum _{u\in ne[v]}{M}_{l+1}\left({\mathbf{h}}_v^l,{\mathbf{h}}_u^l,{\mathbf{x}}_{vu}\right)\right)$$

GraphSage 图采样与聚合(Graph Sample and Aggregate)

MPNN很好地概括了空域卷积的过程，但定义在这个框架下的所有模型都有一个共同的缺陷：卷积操作针对的对象是整张图，也就意味着要将所有结点放入内存/显存中，才能进行卷积操作。但对实际场景中的大规模图而言，整个图上的卷积操作并不现实。GraphSage[2]提出的动机之一就是解决这个问题。

GraphSage利用采样(Sample)部分结点的方式进行学习。当然，即使不需要整张图同时卷积，GraphSage仍然需要聚合邻居结点的信息，即论文中定义的aggregate的操作。这种操作类似于MPNN中的消息传递过程。

$${\mathbf{h}}_v^{l+1}=\sigma \left({\mathbf{W}}^{l+1}\cdot \text{aggregate}\left({\mathbf{h}}_v^l,\left\{{\mathbf{h}}_u^l\right\}\right),\forall u\in ne[v]\right)$$

图结构序列化(PATCHY-SAN)

PATCHY-SAN 算法 [4] 另辟蹊径，它将图结构转换成了序列结构，然后直接利用卷积神经网络在转化成的序列结构上做卷积。

整个流程自底向上：首先根据自定义规则对图里的结点进行排序，然后选择前6个结点，即图中的 1至6；接着我们把这些结点

频域卷积(Spectral Convolution)

频域卷积网络(Spectral CNN)

频域卷积层的状态更新计算公式如下：
$$h_{;j}^{l+1}=\sigma \left(U\sum _{i=1}^{d_l}{\Theta }_{i,j}^l{U}^T{h}_{;i}^l\right)$$

$${\Theta }_{i,j}^l=g_{\theta }=\left[\begin{array}{ccc}{\theta }_1& ...& 0\\ ...& ...& ...\\ 0& ...& {\theta }_N\end{array}\right]$$

切比雪夫网络(ChebNet)

基本的频域卷积网络要计算拉普拉斯矩阵所有的特征值和特征向量，计算量巨大。在论文[16]中提出了切比雪夫网络，它应用切比雪夫多项式 Chebyshev polynomials来加速特征矩阵的求解。假设切比雪夫多项式的第k项是 $T_k$, 频域卷积核的计算方式如下：

切比雪夫多项式是以递归方式定义的一系列正交多项式序列。

$$g_{\theta }=\sum _{k=0}^{K-1}{\theta }_k{T}_k(\tilde{\Lambda }),\text{ where }\tilde{\Lambda }=\frac{2\Lambda }{{\lambda }_{\max }}-I_N$$

那么$T_k$ 怎么来呢，可以由切比雪夫多项式的定义得来:$T_k(x)=2x{T}_{k-1}(x)-T_{k-2}(x)$，递推式的前两项为$T_0(x)=1$以及$T_1(x)=x$。$\tilde{\Lambda }$的作用是让特征向量矩阵归一化到$[-1,1]$之间。

---

参考：
从图(Graph)到图卷积(Graph Convolution): 漫谈图神经网络;