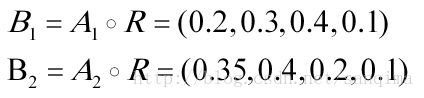用matlab进行模糊综合评判
考虑一个服装评判的问题,为此建立因素集U={u1,u2,u3,u4},其中u1表示花色,u2表示式样,u3表示耐穿程度,u4表示价格,建立评判集V={v1,v2,v3,v4},其中v1表示很欢迎,v2表示较欢迎,v3表示不太欢迎,v4表示不欢迎,进行单因素评判的结果如下:
用模型模型即“主因素决定型”,计算综合评判为:
根据最大隶属度原则可知,第一类顾客对此服装“不太欢迎”,第二类顾客对此服装则“比较欢迎” 。
用matlab解决的代码如下:
%新建Example8_4.m文件
function Example8_4
A1=[0.1 0.2 0.3 0.4];
A2=[0.4 0.35 0.15 0.1];
R=[0.2 0.5 0.2 0.1;
0.7 0.2 0.1 0;
0 0.4 0.5 0.1;
0.2 0.3 0.5 0];
fuzzy_zhpj(1,A1,R)
fuzzy_zhpj(1,A2,R)
end
%%
function[B]=fuzzy_zhpj(model,A,R) %模糊综合评判
B=[];
[m,s1]=size(A);
[s2,n]=size(R);
if(s1~=s2)
disp('A的列不等于R的行');
else
if(model==1) %主因素决定型
for(i=1:m)
for(j=1:n)
B(i,j)=0;
for(k=1:s1)
x=0;
if(A(i,k)
else
x=R(k,j);
end
if(B(i,j)
end
end
end
end
elseif(model==2) %主因素突出型
for(i=1:m)
for(j=1:n)
B(i,j)=0;
for(k=1:s1)
x=A(i,k)*R(k,j);
if(B(i,j)
end
end
end
end
elseif(model==3) %加权平均型
for(i=1:m)
for(j=1:n)
B(i,j)=0;
for(k=1:s1)
B(i,j)=B(i,j)+A(i,k)*R(k,j);
end
end
end
elseif(model==4) %取小上界和型
for(i=1:m)
for(j=1:n)
B(i,j)=0;
for(k=1:s1)
x=0;
x=min(A(i,k),R(k,j));
B(i,j)=B(i,j)+x;
end
B(i,j)=min(B(i,j),1);
end
end
elseif(model==5) %均衡平均型
C=[];
C=sum(R);
for(j=1:n)
for(i=1:s2)
R(i,j)=R(i,j)/C(j);
end
end
for(i=1:m)
for(j=1:n)
B(i,j)=0;
for(k=1:s1)
x=0;
x=min(A(i,k),R(k,j));
B(i,j)=B(i,j)+x;
end
end
end
else
disp('模型赋值不当');
end
end
end
%%
----------------------------------------------------------------------------------
右击“Example8_4.m”-->run,得到如下结果:
ans =
0.2000 0.3000 0.4000 0.1000
ans =
0.3500 0.4000 0.2000 0.1000
------------------------------------------------------------------------------------
解释如下:
根据最大隶属度原则可知,第一类顾客对此服装“不太欢迎”,
第二类顾客对此服装则“比较欢迎” 。