【数据结构与算法分析——C语言描述】第六章：优先队列(堆)
【数据结构与算法分析——C语言描述】第六章：优先队列(堆)
标签（空格分隔）：【数据结构与算法】
第六章：优先队列(堆)
文章目录
- 第六章：优先队列(堆)
- 6.1 模型
- 6.3 二叉堆
- 6.3.1 结构性质
思考如下场景,老师布置了很多作业,现在你需要将作业打印出来,你将作业文件依照队列的形式放入待打印列表中,但此时,你希望最重要(或者是马上就要上交)的作业优先打印出来.此时,队列结构显然不能满足我们的需求,这时候我们考虑一种名为**优先队列(priority queue)**的数据结构,或者称之为堆.
6.1 模型
- 优先队列至少允许以下两种操作:
- Insert(插入)：等价于队列中 Enqueue(入队).
- DeleteMin(删除最小者)：找出、返回和删除优先队列中的最小元素.等价于队列中 Dequeue(出队).
##6.2 一些简单的实现
- 使用一个简单链表再表头以 $ O(1) $ 执行插入操作,并遍历该链表以删除最小元,这需要 $ O(N) $ 的时间.
- 另一种方法,始终让表表示排序转台,这会使得插入操作花费 $ O(N) $ 时间,而 DeleteMin 操作花费 $ O(1) $ 时间.*考虑到 DeleteMin 操作并不多于 Insert 操作,因此在这二者之间,第一种方法可能更好.
- 再一种方法,使用二叉查找树,这样保证了这两种操作的时间复杂度都是 $ O(log N) $ .
尽管插入是随机的,而操作不是,这个结论依旧成立.反复删除左子树的节点会损害树的平衡,但是考虑到右子树是随机的,在最坏的情况下,即 DeleteMin 将左子树删空的情况下,右子树拥有的元素最多也就是它应有的二倍,这只是在期望的深度上增加了一个常数.
6.3 二叉堆
- 二叉堆(binary heap)：如同二叉查找树一样,二叉堆有两个性质, 结构性 和 堆序性 ,如同AVL树一样,对二叉堆的一次操作可能破坏其中一个性质.同时,需要提醒的是,二叉堆可以简称为堆(heap),因为用二叉堆实现优先队列十分普遍.
6.3.1 结构性质
- 完全二叉树(complete binary tree)：完全填满的二叉树,有可能的例外是在底层,底层上的元素从左到右依次填入.如下图.
一棵高度为 $ h $ 的完全二叉树有 $ 2^h $ 到 $ 2^{h+1} - 1 $ 个节点,这意味着,对于拥有 $ N $ 个节点的完全二叉树而言,它的高度为 $ \lfloor logN \rfloor $ ,显然为 $ O(logN) $.
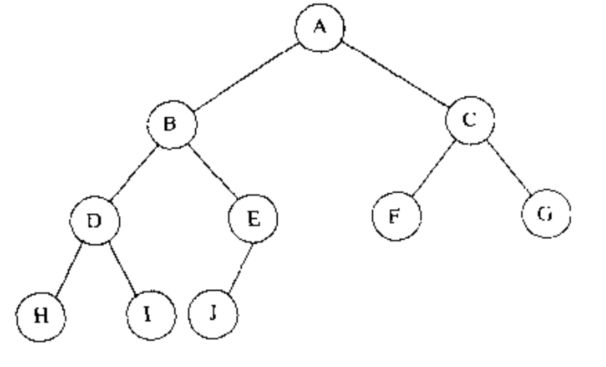
十分重要的一点,由于完全二叉树具有规律性,所以它可以用数组来表示.可以代替指针.如下.
| |A|B|C|D|E|F|J|H|I| J| | | |
–|--|
|0|1|2|3|4|5|6|7|8|9|10|11|12|13|
对于数组中任意一个位置 $ i $ 上的元素,其左儿子在位置 $ 2i $ 上,右儿子在位置 $ 2i + 1 $ 上,它们的父亲在位 置$ \lfloor \frac{i}{2} \rfloor $ 上.
用数组表示的优点不再赘述,但有一个缺点需要提醒,使用数组表示二叉堆需要实现估计堆的大小,但这对于典型情况不成问题.
//优先队列的声明
struct HeapStruct;
typedef struct HeapStruct *PriorityQueue;
struct HeapStruct{
int Capacity;
int Size;
ElementType *Elements;
};
PriorityQueue Initialize( int MaxElements);
void Destroy( PriorityQueue H);
void MakeEmpty( PriorityQueue H);
void Insert( ElementType X, PriorityQueue H);
ElementType DeleteMin( PriorityQueue H);
ElementType FindMin( PriorityQueue H);
int IsEmpty( PriorityQueue H);
int IsFull( PriorityQueue H);
PriorityQueue Initialize( int MaxElements){
PriorityQueue H;
if( MaxElements < MinPQSize)
Error(" Priority queue size is too small");
H = malloc( sizeof( struct HeapStruct));
if( H = NULL)
FatalError(" Out of space");
H->Elements = malloc( ( MaxElements + 1) * sizeof( ElementType));
if( H->Elements == NULL)
FatalError(" Out of space");
H->Capacity = MaxElements;
H->Size = 0;
H->Elements[0] = MinData;//标记
return H;
}
###6.3.2 堆序性质
- 堆序(heap order)：使操作被快速执行的性质,依据堆的性质,最小元总是可以在根处找到.
- 在一个堆中,任意子树也是一个堆.在一个堆中,对于每一个节点 $ X $, $ X $ 的父亲中关键字小于或者等于 $ X $ 中的关键字,根节点除外,因为它没有父亲.
###6.3.3 基本的堆操作
- Insert 插入
考虑将一个元素 $ X $ 插入堆中,我们将在下一个位置建立一个空穴,否则该堆将不再是完全二叉树.
- 如果 $ X $ 可以放到该空穴中而不影响堆的序,那么插入操作完成.
- 否则,我们将这个空穴的父亲节点上的元素移动到该空穴上,这样,空穴便随着根的方向一直向上进行,直到满足步骤 1 为止.这种策略叫上滤(percolate up).如下图所示,尝试插入关键字 14 .
void Insert( ElementType X, PriorityQueue H){
int i;
if( IsFull( H)){
Error(" Priority queue is full");
return ;
}
for( i = ++H->Size; H->Elements[i/2] > X; i/=2)
H->Elements[i] = H->Elements[i/2];
H->Elements[ i] = X;
}
如果插入的元素是新的最小值,那么它将被推到顶端.在顶端, $ i = 1 $ ,我们可以跳出循环,可以在 $ i = 0 $ 处放置一个很小的值使得循环中止.这个值我们称之为标记(sentinel),类似于链表中头节点的使用,通过添加一条哑信息(dummy piece of infomation),避免每次循环都要执行一次测试,从而节省了一点时间.
如果插入的元素是新的最小元,已知过滤到根部,那么这种插入的时间复杂度显然是 $ O(logN) $ .
- DeleteMin 删除最小元
DeleteMin 的操作类似于 Insert 操作.找到最小元是很容易的,而删除它是比较困难的.当删除一个最小元时,在根节点处产生一个空穴,由于现在堆少了一个元素,因此堆中最后一个元素 $ X $ 必须移动到该堆的某个位置.
- 如果 $ X $ 可以移动到空穴中去,那么 DeleteMin 操作完成.
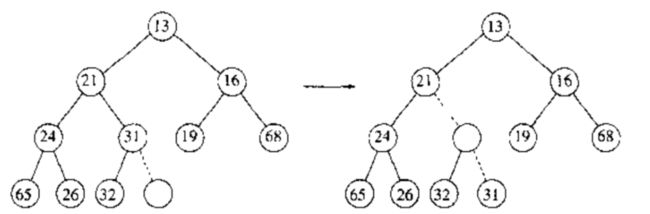
- 鉴于 1. 中的步骤不太可能发生,因此我们考虑 $ X $ 不能移动到空穴中的情况,我们将空穴的两个儿子中较小的一个(考虑到是最小堆)移入空穴中,这样一来就把空穴向下推了一格,重复这个步骤直到 $ X $ 可以被放到空穴中.这种策略叫做下滤(percolate down).如下例:
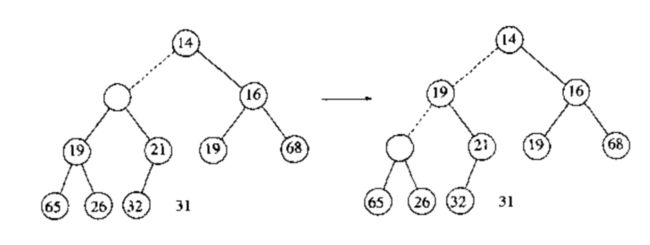
其中需要注意的一点是,当堆中存在偶数个元素时,此时将会遇到一个节点只有一个儿子的情况,我们不必须保证节点不总有两个儿子,因此这就涉及到一个附加节点的测试.
ElementType DeleteMin( PriorityQueue H){
int i, Child;
ElementType MinElement, LastElement;
if( IsEmpty( H)){
Error(" Priority queue is empty");
return H->Elements[0];
}
MinElement = H->Elements[1];
LastElement = H->Elements[ H->Size--];
for( i=1; i*2 <= H->Size; i = Child){
Child = i * 2;
if( Child != H->Size && H->Elements[ Child + 1] < H->Elements[ Child])
Child++;
//if语句用来测试堆中含有偶数个元素的情况
if( LastElement > H->Elements[ Child])
H->Elements[i] = H->Elements[ Child];
else break;
}
H->Elements[i] = LastElement;
return MinElement;
}
这种算法的最坏运行时间为 $ O(logN) $ ,平均而言,被放到根除的元素几乎下滤到堆的底层.
###6.3.4 其他堆的操作
- 对于最小堆(min heap)而言,求最小元易如反掌,但是求最大元,却不得不采取遍历的手段.对于最大堆找最小元亦是如此.
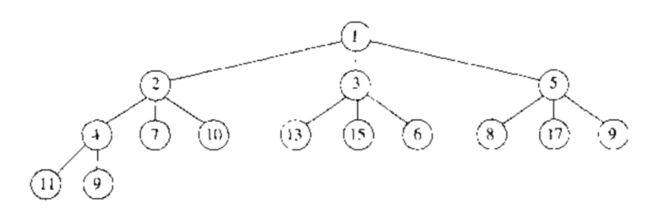
- 事实上,一个堆所蕴含的关于序的信息很少,因此,如果不对堆进行线性搜索,是没有办法找到任何特定的关键字的.为了说明这一点,在下图所示的大型堆结构(具体元素没有给出).
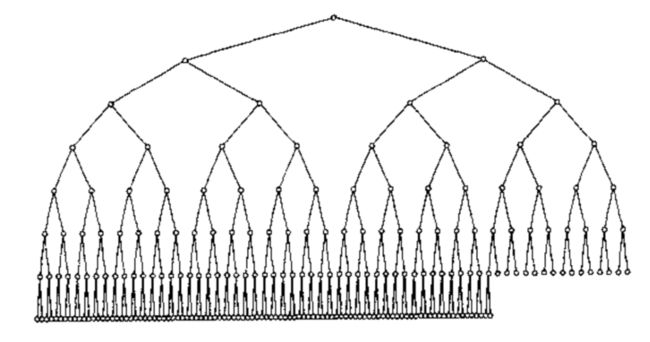
我们看到,关于最大值的元素所知道的唯一信息是:该元素位于树叶上.但是,有近半数的元素位于树叶上,因此该信息是没有什么用处的.出于这个原因,如果我们要知道某个元素处在什么位置上,除了堆之外,还要用到诸如散列表等某些其他的数据结构.
如果我们假设通过某种其他方法得知每一个元素的位置,那么有几种其他的操作的开销将变小.
下列三种这样的操作均以对数最坏情形时间运行.
-
DecreaseKey 降低关键字的值
DecreaseKey(P, $ \Delta $ , H)操作将降低在位置 P 处关键字的值,降低的幅度为 $ \Delta $( $ \Delta > 0 $ ),由于这可能会破坏堆的序,因此必须通过上滤对堆进行调整.该操作堆系统管理程序是游泳的,系统管理程序能够使它们的程序以最高的优先级来运行. -
IncreaseKey 增加关键字的值
IncreaseKey(P, $ \Delta $ , H)操作将增加在位置 P 处关键字的值,增值的幅度为 $ \Delta $( $ \Delta > 0 $ ).可以通过下滤来完成.许多调度程序自动地降低正在过多小号CPU时间的进程的优先级. -
Delete 删除
Delete(P, H)操作删除堆中位置 P 上的节点.这通过首先执行DecreaseKey(P, $ \infty $ , H),然后再执行 DeleteMin(H).当一个进程被用户中止(非正常中止)时,它不许从优先队列中除去. -
BuildHeap 构建堆
BuildHeap(H)操作把 N 个关键字作为输入并把它们放到空堆中.显然,这可以使用 N 个 Insert 操作来完成.由于每个 Insert 操作将会花费平均 $ O(1) $ 时间和最坏 $ O(logN) $ 时间,因此该操作的总的运行时间是 $ O(N) $ 平均时间而不是 $ O(NlogN) $ 最坏情形时间.由于这是一种特殊的执行,没有其他操作的干扰,也让且我们已经直到了该指令能够以线性平均时间运行,因此,期望能够保证线性时间界的考虑是合乎情理的.
下面我们看平均时间是怎么得到的.
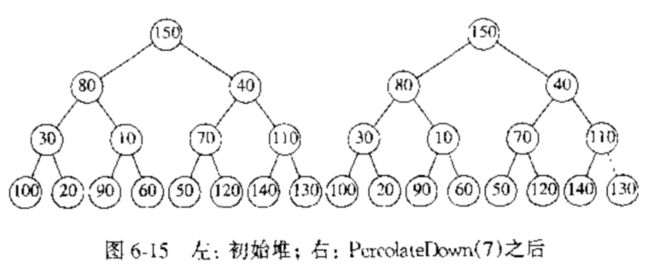
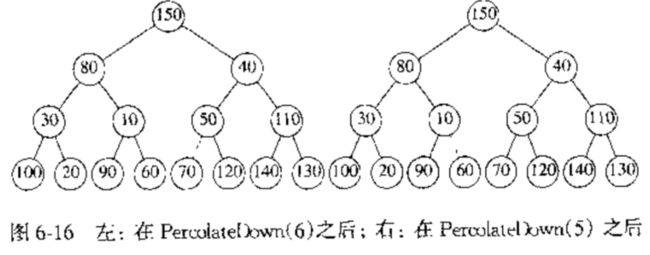
一般的算法是将 N 个关键字以任意顺序放入树中,保持结构特性.此时,如果 percolateDown(i) 从节点 i 下滤,那么执行下列代码创建一棵具有堆序的树(heap-ordered tree)
for( i = N/2; i>0; i--)
PercolateDown(i);
如下例
为了确定 BuildHeap 的运行时间的界,我们确定虚线条数的界,这可以通过计算树中所有节点的高度和来得到,它是虚线的最大条数,现在我们说明,该和为$ O(N) $
- 定理：包含 $ 2^{b+1} - 1 $ 个节点高为 $ b $ 的理想二叉树(perfect binary tree)的节点的高度的和为 $ 2^{b+1} - 1 - ( b + 1 ) $
证明：容易看出以下规律:
| 高度 | 节点数量 |
|---|---|
| b | 1 |
| b-1 | 2 |
| … | … |
| 1 | 2 b − 1 2^{b-1} 2b−1 |
| 0 | 2 b 2^{b} 2b |
则所有节点的高度和 $ S = 2^{0} * b + 2^{1} *( b - 1 ) + … + 2^{b-1} * 1+ 2^{b} * 0 = $
利用裂项相消,得到
$ S = 2^{b+1} - 1 - ( b + 1 ) $
##6.4 优先队列的应用
###6.4.1 选择问题
选择问题(selection problem)：从一组 N 个数而要确定其中第 k 个最大者.
- 算法一: 把这些元素依次读入数组并给他们排序,同时返回适当的元素.该算法的时间复杂度为 $ O(N^2) $
- 算法二：先把前 k 个元素读入数组并按照递减的顺序排序,之后,将剩下的元素逐个读入,当新元素读入时,如果它小于数组中的第 k 个元素则忽略,否则就将它放到数组中正确的位置上.同时将数组中的一个元素挤出数组,当算法中止的时候,第 k 个位置上的元素作为关键字返回即可.该算法的时间复杂度是 $ O(kN) $,当 $ k = \lceil \frac{N}{2} \rceil $ 时,该算法时间复杂度为 $ O(N^2) $ .注意,对于任意的 k ,我们可以求解对称的问题:找出第 (N - k + 1) 个最小的元素,从而 $ k = \lceil \frac{N}{2} \rceil $ 实际上时这两种算法最困难的情况,此时 k 处的值被称为中位数(median).
- 算法三：为简单起见,假设我们只考虑找出第 k 个最小的元素.我们将 N 个元素读入一个数组,然后堆数组应用 BuildHeap 算法,最后,执行 k 次 DeleteMin 操作.从该堆中最后提取的元素就是我们需要的答案.显然,改变堆序的性质,我们可以求原式问题:找出第 k 个最大的元素.
算法的正确性显然.
考虑算法的时间复杂度,如果使用 BuildHeap ,构造堆的最坏情形用时为 $ O(N) $ ,而每次 DeleteMin 用时 $ O(logN) $ .由于有 k 次 DeleteMin,因此我们得到总的运行时间为 $ O(N + klogN) $ .
- 如果 $ k = O(\frac{N}{logN} ) $ ,那么运行时间取决于 BuildHeap 操作,即O(N).
- 对于大的 k 值,运行时间为 $ O(klogN) $.
- 如果 $ k = \lceil \frac{N}{2} \rceil $,那么运行时间为 $ \Theta(NlogN) $
- 算法四：回到原始问题:找出第 k 个最大的元素.在任意时刻我们都将维持 k 个最大元素的集合 S 。在前 k 个元素读入之后,当再读入一个新的元素时,该元素将与第 k 个最大元素进行比较,记这第 k 个最大的元素为 $ S_k $ .注意, $ S_k $ 是集合 S 中最小的一个元素.如果新元素比 $ S_k $ 大,那么用新元素替代集合 S 中的 $ S_k $ .此时,集合 S 中将有一个新的最小元素,它与偶可能是刚刚添加进的元素,也有可能不是.当输入终止时,我们找到集合 S 中的最小元素,并将其返回,这边是答案.
算法四思想与算法二相同.不过,在算法四中,我们用一个堆来实现集合 S ,前 k 个元素通过调用依次 BuildHeap 以总时间 $ O(k) $ 被置入堆中.处理每个其余的元素花费的时间为 $ O(1) + O(logk) $,其中 $ O(1) $ 部分是检查元素是否进入 S 中, O(logk)部分是再必要时删除 $ S_k $ 并插入新元素.因此总时间是 $ O(k + ( N - k )logk) = O( Nlogk) $.如果 $ k = \lceil \frac{N}{2} \rceil $,那么运行时间为 $ \Theta(NlogN) $.
###6.4.2 时间模拟
- 我们假设有一个系统,比如银行,顾客们到达并站队等在哪里直到 k 个出纳员中有一个腾出手来.我们关注在于一个顾客平均要等多久或队伍可能有多长这样的统计问题.
- 对于某些概率分布以及 k 的取值,答案都可以精确地计算出来.然而伴随着 k 逐渐变大,分析明显地变得困难.
- 模拟由处理中的时间组成.这里有两个事件.
- 一个顾客的到达.
- 一个顾客的离开,从而腾出一名出纳员.
- 我们可以使用概率函数来生成一个输入流,它由每个顾客的到达时间和服务时间的序偶组成,并通过到达时间排序.我们不必使用一天中的精准时间,而是通过名为滴答(tick)的单位时间量.
进行这种模拟的一种方法是在启动处在 0 滴答处到额一台摸拟钟表.让钟表一次走一个滴答,同时查询是否有一个事件发生.如果有,那么我们处理事件,搜集统计资料.当没有顾客留在输入流中且所有出纳员都闲置,模拟结束.
但是这种模拟问题,它运行的时间不依赖顾客数量或者时间数量,而是依赖于滴答数,但是滴答数又不是实际输入.不妨假设将时钟的单位改成滴答的千分之一并将输入中的所有时间乘以 1000 ,那么结果便是,模拟用时增加了1000倍.
避免这种问题的关键在于在每一个阶段让重表直接走到下一个事件时间,从概念上来看这是容易做到的.在任一时刻,可能出现的下一个时间或者是下一个顾客到达,或者是有一个顾客离开,同时一个出纳员闲置.由于可以得知将发生事件的所有时间,因此我们只需要找出最近的要发生的事件并处理这个事件. - 如果这个事件是有顾客离开,那么处理过程包括搜集离开的顾客的统计资料及检验队列看看是否还有其他顾客在等待.如果有,那么我们加上这位顾客,处理所需要的统计资料,计算该顾客将要离开的时间，并将离开事件假到等待发生的事件集中区.
- 如果事件是有顾客到达，那么我们检查闲置的出纳员.如果没有，那么我们把该到达时间放置到队列中去；否则，我们分配顾客一个出纳员，计算顾客离开的时间，并将离开事件加到等待发生的事件集中区.
在等待的顾客队伍可以实现为一个队列.由于我们需要找到最近的将要发生的事件，合适的办法是将等待发生的离开的结合编入到一个优先队列中.下一个事件是下一个到达或者下一个离开. - 考虑以上算法的时间复杂度，如果有 C 个顾客（因此有 2C 个事件 ）和 k 个出纳员，那么模拟的运行时间将会是 $ O( Clog(k+1)) $ ,因为计算和处理每个事件花费时间为 $ O(logH) $ ,其中 $ H = k + 1 $ 为堆的大小.
##6.5 d-堆
- d-堆是二叉堆的推广，它像一个二叉堆，但是所有的节点都有 d 个儿子（注意，二叉堆是一个2-堆）.
如上图所示，3-堆。
##6.6 左式堆
- Merge 合并操作，堆而言，合并操作是最困难的操作。
- 考虑到堆结构无法用数组实现以 $ O(N) $ 高效的合并操作。因此，所有支持高效合并的高级数据结构都需要使用指针。
- 左式堆(leftist heap)：它与二叉树之间的唯一区别是，左式堆不是理想平衡的，而实际上是趋向于非常不平衡。它具有相同的堆序性质，如有序性和结构特性。
###6.6.1 左式堆的性质
- 零路径长(null path length, NPL)：从任一节点 $ X $ 到一个没有两个儿子的节点的最短路径长。因此，具有 0 个或 1 个儿子的节点的 Npl 为 0，而 Npl(NULL) = -1.
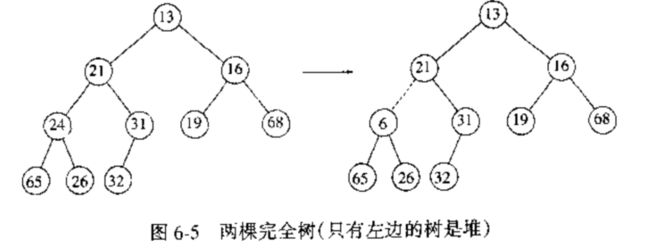
注意，任一节点的零路径长比它诸儿子节点的零路径长的最小值多 1 。这个结论也适用少于两个儿子的节点，因为 NULL 的零路径长为 -1 . - 性质：对于左式堆中的每一个节点 $ X $ ,左则日子的零路径长至少与右儿子的零路径长一样大。如下图所示：
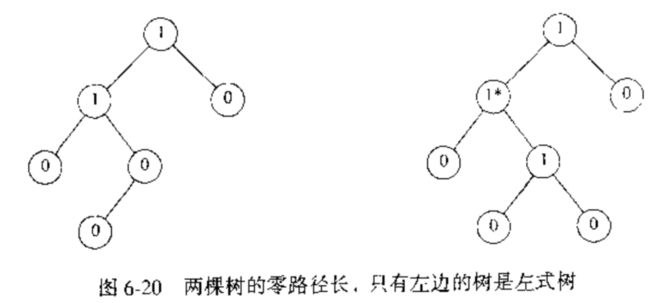
在图示中，右边的树并不是左式堆，因为他不满足左式堆的性质。
左式堆的性质显然更加使树向左增加深度。确实有可能存在由左节点形成的长路径构成的树（实际上这更加便于合并操作），故此，我们便有了左式堆这个名称。
-
定理：
在右路径上有 $ r $ 个节点的左式树必然至少有 $ 2^r - 1 $ 个节点。
证明：数学归纳法。
若$ r = 1 $ ，则必然至少存在一个树节点；
假设定理对 $ r = k $ 成立，考虑在右路径上有 $ k + 1 $ 个节点的左式树，此时，根具有在右路径上含 $ k $ 个节点的右子树，以及在右路径上至少包含 $ k $ 个节点的左式树（否则它便不是左式树）。对这两个子树应用归纳假设，得知每棵子树上最少含有 $ 2^k - 1 $ 个节点，再加上根节点，于是这颗树上至少有有 $ 2^{k+1} - 1 $ 个节点。
原命题得证。 -
推广：从上述定理我们立即可以得到，$ N $ 个节点的左式树有一条右路径最多包含 $ \lfloor log(N+1) \rfloor $ 个节点。
###6.6.1 左式堆的操作
- 合并
首先，注意，插入只是合并的一个特殊情形。首先，我们给出一个简单的递归解法，然后介绍如何能够非递归地施行该解法。如下图，我们输入两个左式堆 $ H_1 ， ， ， H_2 $.
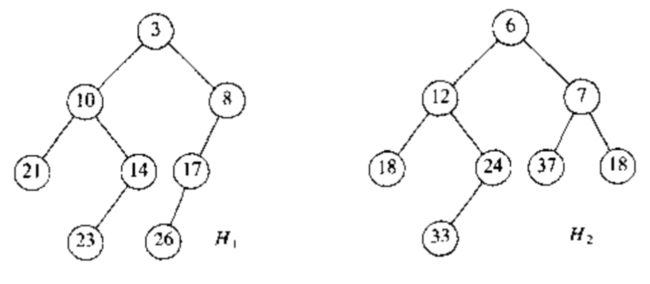
除去使用数据、左指针、右指针外还需要一个只是零路径长的项。
-
如果这两个堆中有一个是空的，那么我们可以直接返回另一个非空的堆。
-
否则，想要合并两个堆，我们需要比较它们的根。回想一下，最小堆中根节点小于它的两个儿子，并且子树都是堆。我们将具有大的根值得堆与具有小的根值得堆的右子树合并。在本例中，我们递归地将 $ H_2 $ 与 $ H_1 $ 中根在 8 处的右子堆合并，得到下图：
-
注意，因为这颗树是通过递归形成的，我们有理由说，合成的树依然是一棵左式树。现在，我们让这个新堆成为 $ H_1 $ 中根的右儿子。如下图：
-
最终得到的堆依然满足堆序的性质，但是，它并不是左式堆。因为根的左子树的零路径长为 1 ，而根的右子树的零路径长为 2 .左式树的性质在根处遭到了破坏。不过，很容易看到，树的其余部分必然是左式树。这样一来，我们只要对根部进行调整即可。
方法如下：只要交换根的做儿子和右儿子，如下图，并更新零路径长，就完成了 Merge . 新的零路径长是新的右儿子的零路径长加 1 .注意，如果零路径长不更新，那么所有的零路径长将都是 0 ，而堆也不再是左式堆，只是随机的。
struct TreeNode;
typedef struct TreeNode *PriorityQueue;
struct TreeNode{
ElementType Element;
PriorityQueue Left;
PriorityQueue Right;
int Npl;
};
PriorityQueue Initialize( void);
ElementType FindMin( PriorityQueue H);
int IsEmpty( PriorityQueue H);
PriorityQueue Merge( PriorityQueue H1, PriorityQueue H2);
PriorityQueue Merge1( PriorityQueue H1, PriorityQueue H2)
#define Insert( X, H)( H = Insert1( ( X), H)
//宏Insert 完成一次与二叉堆兼容的插入操作
PriorityQueue Insert1( ElementType X, PriorityQueue H);
//Insert1 左式堆的插入例程
PriorityQueue DeleyeMin1( PriorityQueue H);
//合并
PriorityQueue Merge( PriorityQueue H1, PriorityQueue H2){
if( H1 == NULL)
return H2;
if( H2 == NULL)
return H1;
if( H1->Element < H2->Element);
return Merge1( H1, H2);
else
return Merge1( H2, H1);
}
PriorityQueue Merge1( PriorityQueue H1, PriorityQueue H2){
if( H1->Left == NULL)
H1->Left = H2;
else{
H1->Right = Merge( H1->Right, H2);
if( H1->Left->Npl < H1->Right->Npl)
SwapChildren( H1);
H1->Npl = H1->Right->Npl + 1;
}
return H1;
}
//插入
PriorityQueue Insert1( ElementType X, PriorityQueue H){
PriorityQueue SingleNode;
SingleNode = malloc( sizeof( struct TreeNode));
if( SingleNode == NULL)
FatalError(" Out of space");
else{
SingleNode->Element = X;
SingleNode->Npl = 0;
SingleNode->Left = SingleNode->Right = NULL;
H = Merge( SingleNode, H);
}
return H;
}
//删除
PriorityQueue DeleyeMin1( PriorityQueue H){
PriorityQueue LeftHeap, RightHeap;
is( IsEmpty( H)){
Error(" Priority queue is empty");
return H;
}
LeftHeap = H->Left;
RightHeap = H->Right;
free( H);
return Merge( LeftHeap,RightHeap);
}
##6.7 斜堆
- 斜堆(skew heap)：斜堆是具有堆序的二叉树，但是不存在对树的结构限制。它是左式堆的自调节形式，但不同于左式堆，关于任意节点的零路径长的任何信息不做保留。斜堆的右路径在任何时候都可以任意长，因此，所有操作的最坏情形运行时间为 $ O(N) $ .
与左式堆相同，斜堆的基本操作也是 Merge 合并。但是有一处例外，对于左式堆，我们查看是否左儿子和右儿子满足左式堆堆序性质并交换那些不满足性质者；对于斜堆，除了这些右路径上所有节点的最大者不交换它们的左右儿子之外，交换是无条件的。
##6.8 二项队列
###6.8.1 二项队列结构
- 二项队列(binomial queue)：一个二项队列不是一棵堆序的树，而是堆序树的集合，称为森林(forest).
- 堆序树中的每一棵都是有约束的形式，叫做二项树（binomial tree）.
- 每一个高度上之多存在一棵二项树。高度为 0 的二项树是一颗单节点树；高度为 k 的二项树 $ B_k $ 是通过将一棵二项树 $ B_{k-1} $ 附接到另一棵二项树 $ B_{k-1} $ 的根上而构成的。如下图：二项树 $ B_0、B_1、B_2、B_3、B_4 $ .
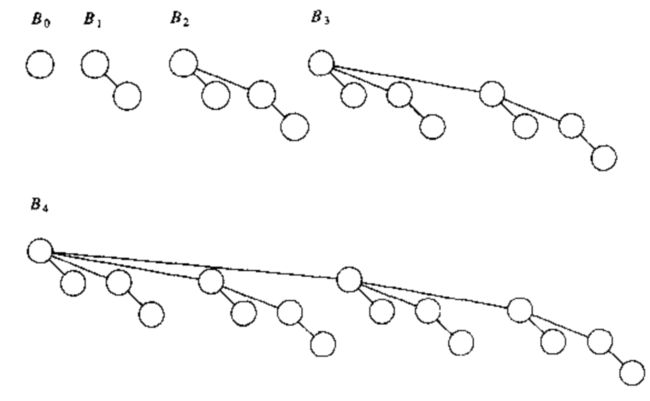
从图中看到，二项树 $ B_k $ 由一个带有儿子 $ B_0 , B_1, B_2,…, B_{k-1} $ 的根组成。高度为 k 的二项树恰好有 $ 2^k $ 个节点，而在深度 d 处的节点数为 $ C_k^d $ .
- 如果我们把堆序施加到二项树上并允许任意高度上最多有一棵二项树，那么我们能够用二项树的集合惟一地表示任意大小地优先队列。
for example：大小为 13 的优先队列可以用森林 $ B_0 , B_2, B_3 $ 表示。我们可以把这种表示写成 1101 ，这不仅以二进制表示了 13 也表述 $ B_1 $ 树不存在的事实。
###6.8.2 二项队列的操作
-
FindMin：可以通过搜索所有树的树根找出。由于最多有 $ logN $ 棵不同的树，因此找到最小元的时间复杂度为 $ O(logN) $ . 另外，如果我们记住当最小元在其他操作期间变化时更新它，那么我们也可保留最小元的信息并以 $ O(1) $ 时间执行该操作。
-
Merge：合并操作基本上是通过将两个队列加到一起来完成的。考虑两个二项队列 $ H_1,H_2 $ ,他们分别具有六个和七个元素，见下图。
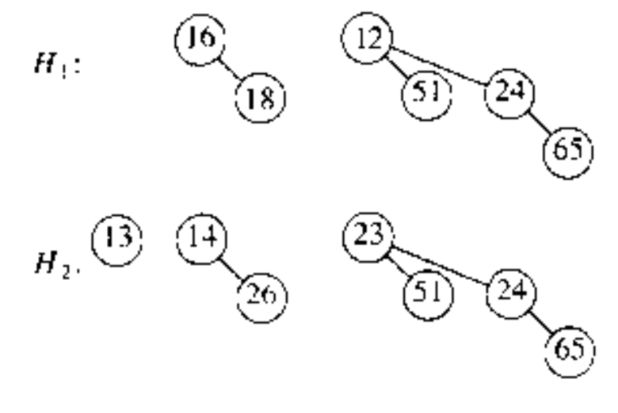
令 $ H_3 $ 是新的二项队列。 -
由于 $ H_1 $ 没有高度为 0 的二项树而 $ H_2 $ 拥有，因此我们就用 $ H_2 $ 中高度为 0 的二项树作为 $ H_3 $ 的一部分。
-
由于 $ H_1、H_2 $ 都拥有高度为 1 的二项树，因此我们令二者合称为 $ H_3 $ 中高度为 2 的二项树。
-
现存有三棵高度为 2 的树，我们选择其中两个和合成高度为 3 的树，另外一棵放到 $ H_3 $ 中。
-
由于现在 $ H_1、H_2 $ 不存在高度为 3 的树，合并结束。
$ H_3 $ 如下图：
考虑 Merge 操作的时间复杂度，由于几乎使用任意合理的实现方法合并两棵二项树均花费常数时间，而总存在 $ O(logN) $ 棵二项树，因此合并在最坏情形下花费时间为 $ O(logN) $ .为了使操作更高效，我们需要将这些树放到按照高度排血的二项队列中。
-
Insert：插入操作实际上是特殊情形的合并，我们只需要创建一棵单节点树并执行一次合并操作。这种操作的最坏运行时间也是 $ O(logN) $ .更加准确地说，如果元素将要插入的那个优先队列不存在的最小的 $ B_k $ ,那么运行时间与 i+1 成正比.
-
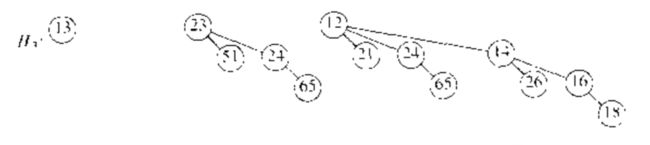
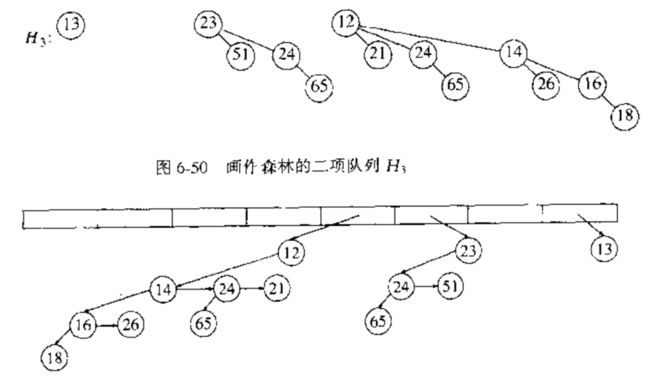
DeleteMin：通过首先找出一棵具有最小根的二项树来完成。令该树为 $ B_k $ ,并令原始的优先队列为 $ H $ ,我们从 H 的树的森林中除去二项树 $ B_k $ ,形成新的二项树队列 $ H’ $ ,再除去 $ B_k $ 的根，得到一些二项树 $ B_0 , B_1, B_2,…, B_{k-1} $ ,它们共同形成优先队列 $ H’’ $ .合成 $ H’ $ 与 $ H’’ $ ,操作结束。
例如，假设有二项队列 $ H_3 $ ,如下图：
其中最小的根是 12，因此我们得到两个优先队列 $ H’ $ 和 $ H’’ $ ,如下图：
最后，合并 $ H’ $ 和 $ H’’ $ ,完成 DeleteMin 操作。
分析时间复杂度，注意，DeleteMin 操作将原队列一分为二，找出含有最小元素的树并创建队列 $ H’ $ 和 $ H’’ $ 花费时间为 $ O(logN) $ 时间，合并 $ H’ $ 和 $ H’’ $ 又花费时间为 $ O(logN) $ 时间。因此，整个 DeleteMin 操作的时间复杂度为 $ O(logN) $ .
###6.8.3 二项队列的实现
- 二项树的每一个节点包含一个数据，第一个儿子以及右兄弟。二项树中的诸儿子以递增的次序排列。
//声明
typedef struct BinNode *Position;
typedef struct Collection *BinQueue;
struct BinNode{
ElementType Element;
Position LeftChild;
Position NextSibling;
};
struct Collection{
int CurrentSize;
BinTree TheTrees[ MaxTrees];
};
//合并两颗同样大小的二项树
BinTree CombineTrees( BinTree T1, BinTree T2){
if( T1->Element > T2->Element)
return ConbinTrees( T2, T1);
T2->NextSibling = T1->LeftChild;
T1->LeftChild = T2;
return T1;
}
//合并
BinQueue Merge( BinQueue H1, BinQueue H2){
BinTree T1, T2, Carry = NULL;
int i,j;
if( H1->CurrentSize + H2->CurrentSize > Capacity)
Error("Merge would exceed capacity");
H1->CurrentSize += H2->CurrentSize;
for( i = 0, j = 1; j <= H1->CurrentSize; i++){
T1 = H1->TheTrees[i];
T2 = H2->TheTrees[i];
switch( !!T1 + 2 * !!T2 + 4 * !!Carry){//Carry 是上一步骤得到的树
case 0: //No trees;
case 1:
break;
case 2:
H1->TheTrees[i] = T2;
H2->TheTrees[i] = NULL;
case 4: //Only Carry
H1->TheTrees[i] = Carry;
break;
case 3:
Carry = CombineTrees( T1, T2);
H1->TheTrees[i] = H2->TheTrees[i] = NULL;
break;
case 5:
Carry = CombineTrees( T1, T2);
H1->TheTrees[i] = NULL;
break;
case 6:
Carry = CombineTrees( T1, T2);
H2->TheTrees[i] = NULL;
break;
case 7: //All three
H1->TheTrees[i] = Carry;
Carry = CombineTrees( T1, T2);
H2->TheTrees[i] = NULL;
break;
}
}
return H1;
}
//删除最小元并返回
ElementType DeleteMin( BinQueue H){
int i,j;
int MinTree;
BinQueue DeletedQueue;
Position DeletedTree, OldRoot;
ElementType MinItem;
if( IsEmpty( H)){
Error(" Empty binimial queue");
return -Infinity;
}
MinItem = Infinity;
for( i = 0; i< MaxTrees; i++){
if( H->TheTrees[i] && H->TheTrees[i]->Element < MinItem){
MinItem = H->TheTrees[i]->Element;
MinTree = i;
}
}
DeletedTree = H->TheTrees[MinTree];
OldRoot = DeletedTree;
DeletedTree = DeletedTree->LeftChild;
free(OldRoot);
DeletedQueue = Initialize();
DeletedQueue->CurrentSize = ( 1<< MinTree) - 1;
for( j = MinTree - 1; j >= 0; j--){
DeletedQueue->TheTrees[j] = DeletedTree;
DeletedTree = DeletedTree->NextSibling;
DeletedQueue->TheTrees->NextSibling = NULL;
}
H->TheTrees[ MinTree] = NULL;
H->CurrentSize -= DeletedQueue->CurrentSize + 1;
Merge( H, DeletedQueue);
return MinItem;
}
##我的微信公众号
