【算法】第一章:基础
【算法】第一章:基础
标签(空格分隔):【Java算法】
第一章:基础
文章目录
- 第一章:基础
- 1.1 基础编程模型
- 1.2 数据抽象
- 1.3 背包、队列、栈
- 1.4 算法分析
- 1.5 案例分析:union-find 算法
- 我的微信公众号
1.1 基础编程模型
一段Java程序(类)或者是一个静态方法(函数)库,或者定义一个数据类型。要创建静态方法库,会用到以下七种语法。
- 原始数据类型:在计算机中精确地定义整数、浮点数和布尔值等。它们的定义包括取值范围和能够对相应的值进行的操作,它们能够被组合为类似于数学公式定义的表达式。
- 语句:语句通过创建变量并对其赋值、控制运行流程或引发副作用来进行计算。六种语句包括:声明、赋值、条件、循环、调用、返回。
- 数组:多个同种数据类型的值的集合。
- 静态方法:静态方法可以封装并重用代码,使我们可以使用一些独立的模块来开发程序。
- 字符串:一串连续的字符。
- 标准输入/输出:程序与外接联系的桥梁。
- 数据抽象:数据抽象封装和重用代码,使我们可以定义非原始数据类型,进而支持面向对象的编程。
四种最基本的Java原始数据类型:
- 整型 int
- 双精度实数类型 double
- 布尔型 boolean
- 字符型 char
Java 程序控制是使用 标识符 来命名的变量。每一个变量都有自己的类型并存储了一个合法的值。
Java中,使用表达式来进行各种类型的操作。
对于原始类型而言,使用标识符来引用变量;用+,-,*,/等运算符来指定操作;用字面量来表示对值的操作。
| 术语 | 例 |
|---|---|
| 原始数据类型 | int double boolean char |
| 变量 | [任意标识符] |
| 运算符 | +; -; *; / |
| 字面量 | 1-2; true; ‘a’; 1.2, 1.0e |
| 表达式 | lo<=hi; (hi-lo)/2; |
| 类型 | 值域 | 运算符 |
|---|---|---|
| int | 32位二进制补码 | +,-,*,/,% |
| double | 双精度实数 | +,-,*,/ |
| boolean | true, flase | &&, ||, !, ^ |
| char | 字符 |
- Java中使用中缀表达式。并且具有优先级顺序的区别。
- 类型转换:不损失信息时,树枝会被自动提升为高级的数据类型。需要注意的是,浮点数转整数时会舍去小数部分,而不是四舍五入。
- 比较:==, !=, <, <=, >, >=. 结果为布尔型。
- 为了灵活性,Java还提供了其他集中原始数据类型:64位整数long; 16为整数short; 16位字符char; 8位整数byte; 32位单精度浮点数float.
| 语句 | 定义 |
|---|---|
| 声明语句 | 创建一个指定类型的变量并用标识符命名 |
| 赋值语句 | 将某一数据类型的值赋予给一个变量 |
| 声明并初始化 | 在声明时赋予变量初始值 |
| 隐形赋值 | 形如i++, i+=1 |
| 条件语句if | 根据布尔表达式的值执行一条语句 |
| 条件语句if-else | 根据布尔表达式的值执行两条语句中的一条 |
| 循环语句(while\for) | 执行语句,直到布尔表达式中为false |
| 调用语句 | |
| 返回语句 |
- 数组:顺序存储相同类型的多种数据。
- 索引:访问数组的编号。
- 创建并初始化数组三步骤:声明数组的名字和类型、创建数组、初始化数组元素。
//Java中三种创建数组的模式
//完整模式
double[] test; //声明数组
test = new double[ N]; //创建数组
for( int i = 0;i < N; i++) //初始化数组
test[i] = 0.0;
//简化写法
double[] test = new double[N];
//声明初始化
int[] test = {1,2,3,4,5,6};
- 数组的别名:数组名表示的是整个数组,如果将数组变量赋予给另外一个变量,则两个变量名会指向同一个数组。这样做有时会带来许多难以察觉的问题。
例如:
int[] a = new int[N];
a[0] = 1234;
int[] b = a;
b[0] = 56789;//此时a[0]的值也会变成56789
-
数组的复制:如果想复制数组,那么应该声明、创建、初始化一个新的数组,然后将原数组中的元素值一个一个地复制到新的数组中。
-
二维数组:例如:
int[][] a = new int[M][N];其中,第一维M为行数,N为列数。
注意,和一维数组一样,默认的数组元素的值为0, boolean型数组元素默认为false.
- 静态方法:本文章中所有Java程序要么是数据类型的定义,要么是一个静态方法库.
静态方法被称为函数,例如下列代码为一个静态函数,下列代码是使用牛顿迭代法计算平方根。
public static double sqrt( double c){
if( c < 0)
return Double.NaN;
double t = c;
double err = 1e-15;
while( Math.abs( t - c/t) > err * t)
t = ( c/t + t) /2.0;
return t;
}
//签名: public static double sqrt( double c)
//返回值类型: double
//方法名: sqrt
//参数类型: double ; 参数变量: c
//返回语句: return t;
//函数体
//局部变量
-
调用静态方法:写出方法名并在后面的括号中列出参数值,用逗号分割。
-
方法的性质:1. 方法的参数值按值传递。2. 方法名可以被重载。3. 方法只能返回一个值,但可以有多条返回语句。4. 方法可以产生副作用。
-
递归:包括基准情况和递归方程。注意,递归调用的父问题和尝试解决的子问题之间不应该有交集。
-
静态方法库:在Java中,类的声明是
public class 类名{}.存放类的文件的文件名和类名相同,扩展名为.java。 Java的基本开发模式是编写一个静态方法库来完成一个任务。输入java和类名以及一席勒字符串就能调用类中的main()方法,其参数为由输入的字符串组成饿一个数组。 -
模块化编程:
-
单元测试:Java编程的最佳实践之一是每一个静态方法库中都包含一个mian()函数来测试库中的所有方法。每个模块的main()方法至少应该调用模块中的其他代码并在某种程度上保证它的正确性。
-
外部库:1. 系统标准库:java.lang.*,例如Math、Integer、Double、string、StringBuilder、System; 2. 导入的库,例如java.util.Arrays. 要在程序开头使用import语句导入才能使用这些库。3. 其他库,若使用这些苦,应下载相应源代码放到工作目录中。
- API: 即应用程序编程接口。例如:
| 库名 | 方法(简略) |
|---|---|
| Math | abs, max, min, sin, cos, tan, exp, log, pow, random,sqet, E,PI; |
| SetRandom | setSeed, random, uniform, bernoulli, gaussian, discrete, shuffle |
| StdStats | max, min, mean, var, setdev, median |
- 字符串:由一串字符(char类型)组成的。一个String类型的字面量包括一堆双引号和其中的字符,例如
"Hello World". 需要注意的是,String虽然是Java的一个数据类型,但并不是原始数据类型。
String拼接:+. 若仅一个参数为字符串,Java会自动将其他参数全部转换为字符串。
类型转换:将字符串转换为整数:parseInt;将整数转换为字符串toString;将字符串转换为浮点数parseDuble;将浮点数转换为字符串toString.
命令行参数:Java中字符串一个重要用途是使程序能够接受到从命令行传递来的信息。当输入命令java和一个库名以及一系列字符串之后,Java系统会调用库的main()方法并将一系列字符串转变为一个数组作为参数传递给他。
Java可以从命令行参数或标准输入流的抽象字符流中获得输入,并从标准输出流中输出。
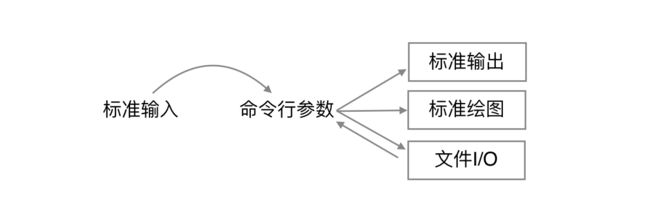
- 操作系统常用命令:
| 命令 | 参数 | 作用 |
|---|---|---|
| javac | .java文件名 | 编译Java程序 |
| java | .class文件名(不需要扩展名)和命令行参数 | 运行Java程序 |
| more | 任意文本文件名 | 打印文件内容 |
- 标准输出库的静态方法的API:
| public class StdOut//若使用StdOut, 则应该先下载StdOut.java到工作目录 |
|---|
| static void print(String s) //打印s |
| static void println(String s) //打印s并接一个换行符 |
| static void println() //打印换行符 |
| static void printf(String f,…) //格式化输出 |
- 标准输入库的静态方法的API:
| public class StdIn |
|---|
| static boolean isEmpty() //若输入流中无剩余值则返回true |
| static int readInt() |
| static long readLong() |
| static double readDouble() |
| static float readFloat() |
| static boolean readBoolean() |
| static char readChar() |
| static byte readByte() |
| static String readString() |
| static boolean hasNextLine() //输入流是否还有下一行 |
| static String readLine() //读取该行中的其余内容 |
| static String readAll() //读取输入流的其余内容 |
-
重定向:
%java RandomSeq 1000 100.0 200.0 > data.txt这条指令致命标准输入流被写入一个data.txt文件中。

-
管道:
%java Average < data.txt这条命令从文件data.txt中读取一系列数值并计算它们的平均值。 -
用于读取和写入数组的静态方法的API:
| public class Out |
|---|
| static void write(int[] a, String name) |
| static void write(double[] a, String name) |
| static void write(String[] a, String name) |
| public class In |
|---|
| static int[] readInts(String name) |
| static double[] readDoubles(String name) |
| static String[] readStrings(String name) |
- 标准绘图库:标准绘图抽象层实现在库StdDraw中,设备可以使用该库画一些简单的图形,
| public class StdDraw |
|---|
| static void line(double x0, double y0, double x1, double y1) |
| static void point(double x, double y) |
| static void text(double x, double y, String s) |
| static void circle(double x, double y, double r) |
| static void filledCircle(double x, double y, double r) |
| static void ellipse(double x, double y, double rw,double rh) |
| static void filledEllipse(double x, double y, double rw,double rh) |
| static void square(double x, double y, double r) |
| static void filledSquare(double x, double y, double r) |
| static void rectangle(double x, double y, double rw,double rh) |
| static void filledRectangle(double x, double y, double rw,double rh) |
| static void polygon(double[] x, double[] y) |
| static void filledPolygon(double[] x, double[] y) |
| //当然在StdDraw库中还包含一些控制方法API: |
| static void setXscale(double x0, double x1) |
| static void setYscale(double y0, double y1) |
| static void setPenRadius(double r) |
| static void setPenColor(Color c) |
| static void setFont(Font f) |
| static void setCanvasSize(int w, int h) |
| static void clear(Color c) |
| static void show(int dt) //显示所有图像并暂停dt毫秒 |
-
二分查找:一种高效的查找算法,该静态方法可以在一个已排序的数组中以O(logN)的运行时间找到目标元素,返回其索引。
-
白名单过滤:将一个数据存放到一个文件中,便称为白名单,若输入中存在与该文件中任何数据无关的数据,则便不输出该数据。
-
什么是Java的字节码?
答:它是程序的一种低级表示,可以运行于Java虚拟机。将程序抽象为字节码可以保证Java的跨平台性。 -
Math.abs( -2147483648)的返回值是什么?
答:由于发生了溢出,所以上式结果为-2147483648. -
如何将double类型变量初始化为无穷大?
答:可以使用Java内置常数: Double.POSTIVE_INFINITY, Double.NEGATIVE_INFINITY. -
double类型可以与int类型相互比较吗?
答:如果不进行类型转化是不行的。但是Java一般会自动进行所需要的类型转换。 -
如果使用变量前没有将它初始化,会造成什么结果?
答:Java会抛出一个编译异常。 -
Java表达式中 1/0 和 1.0/0.0 的值是什么?
答:1/0会产生除零异常,此时程序发生终止。1.0/0.0的结果是Infinity. -
String变量能使用 < 和 > 吗?
答:不同于c++, 在Java中,只有原始数据类型才定义了 <,>这些运算符。 -
负数的除法和余数的结果是什么?
答:表达式a/b的商会向0取整,a%b的余数的定义式 (a/b)*b+a%b == a. -
&& 与 & 的区别。
答:运算符 &, |, ^表示整数的位运算操作。 运算符&&, ||仅在布尔表达式中有效。 -
嵌套if的二义性:
答:与C/C++一样,Java中if-else的else满足最近邻原则。 -
int[] a 与 int a[] 有什么区别,为什么有些Java程序员使用int a[]?
答:在Java中,上述两个表达式均合法且等价。但是Java提倡使用int[] a, 因为这种形式更能说明这是一个数组。 -
若程序的标准输入为空,但是仍然常数读取,会发生什么?
答:会发生一个错误。 -
Java中,一个静态方法能够将另外一个静态方法作为参数吗?
答:不行。
1.2 数据抽象
- 数据类型:指一组值和一组对这些值操作的集合。
- 数据抽象:在原始数据类型智商的更高层次的抽象。
- 引用类型:Java编程的基础是使用class关键字构造的引用数据类型,也被称为面向对象编程,因为其核心是对象,即保存了某一个数据类型的值的实体。Java使用术语引用类型来表示与原始数据类型的区别。
- 抽象数据类型(ADT):能够对使用者隐藏数据表示的数据类型。抽象数据类型与静态方法实现的库的不同之处主要在于,ADT将数据和函数的实现关联起来,并将数据的表示方法进行了隐藏。使用ADT时,buoying关心数据的表示实现ADT时,关注数据本身及其操作。
- 对象:对象是能够承载数据类型值的实体。对象具有三个重要的特征:状态、标识、行为。状态即数据类型的值;标识能够将一个对象区别于另外一个对象;行为就是数据类型的操作。
- 创建对象:即创建它的表示。使用new关键字出发构造函数并创建对象,初始化对象中的值并返回它的引用。
- 操作对象中的值:即控制对象的行为,可能改变对象的状态。使用和对象关联的变量调用实例方法来对对象中的值进行操作。
- 操作多个对象:创建对象数组,像原始数据类型一样将它们传递给方法或者从方法中返回,只是变量关联的是对象的引用而不是对象本身。
可能需要用到的数据类型的分类:1. java.lang.*中的标准系统抽象数据类型,可以被任意Java程序调用。2. Java标准库中的抽象数据类型,例如java.swt, java.net, java.io 等,它们也可以被任意Java程序调用,但是需要import语句。3. I/O处理类抽象数据类型,允许处理多个输入输出流。4. 面向对象类抽象数据类型,通过封装数据的表示简化数据的组织和处理。5. 集合类抽象数据类型,简化对同一类型的一组数据的操作。6. 面向操作的抽象数据类型,用来分析各种算法。7. 图算法相关的抽象数据类型,用来封装各种图的表示的面向数据的抽象数据类型,和一些提供图的处理算法的面向操作的抽象数据类型。
| java.lang中的标准Java系统类型 |
|---|
| Integer //int的封装类 |
| Double //double的封装类 |
| String //可由索引访问的char值序列 |
| StringBuilder // 字符串构造类 |
| 其他Java数据类型 |
|---|
| java.awt.Color //颜色 |
| java.awt.Font //字体 |
| java.net.URL //URL |
| java.io.File //文件 |
| Robert Sedgewick创建的库 |
|---|
| In //输入流 |
| Out //输出流 |
| Draw //绘图类 |
| 面向数据的数据类型 |
|---|
| Point2D //平面上的点 |
| Interval1D //一维间隔 |
| Interval2D //二维间隔 |
| Date //日期 |
| Transaction //交易 |
| 用于算法分析的数据类型 |
|---|
| Counter //计数器 |
| Accumulator //累加器 |
| VisulAccumulator //可视累加器 |
| Stopwatch //计时器 |
| 集合类数据类型 |
|---|
| Stack //下压栈 |
| Queue //先进先出队列 |
| Bag //包 |
| MinPQ MaxPQ //优先队列 |
| IndexMinPQ IndexMaxPQ //索引优先队列 |
| ST //符号表 |
| SET //集合 |
| StringST //符号表(字符串键) |
| 面向数据的图数据类型 |
|---|
| Graph //无向图 |
| Digraph //有向图 |
| Edge //加权边 |
| EdgeWeightedGraph //加权无向图 |
| DirectedEdge //有向加权边 |
| EdgeWeightedDigraph //有向加权图 |
| 面向操作的图数据类型 |
|---|
| UF //动态连通性 |
| DepthFirstPathes //路径的深度优先搜索 |
| CC //连通分量 |
| BreadthFirstPaths //路径的广度优先搜索 |
| DirectedDFS //有向图路径的深搜 |
| DirectedBFS //有向图路径的广搜 |
| TransitiveClosure //所有路径 |
| Topological //拓扑排序 |
| DepthFirstOrder //深搜顶点被访问的顺序 |
| DirectedCycle //换的搜索 |
| SCC //强连通分量 |
| MST //最小生成树 |
| SP //最短路径 |
几何对象:这里介绍几种常见的几何对象的ADT. 需要注意的是,实现这些操作具有一定难度。
| public class Point2D |
|---|
| Point2D(double x, double y) //创建一个平面上的点 |
| double x() //x坐标 |
| double y() //y坐标 |
| dpuble r() //极径 |
| double theta() //极角 |
| double distTo( Point2D that) //欧式距离 |
| void draw() //用StdDraw绘制该点 |
| public class Interval1D |
|---|
| Interval1D(double lo, double hi) //创建一个间隔 |
| double length() //间隔长度 |
| boolean contains(double x) //x是否在间隔中 |
| boolean intersect(Interval1D that) //两个间隔是否相交 |
| void draw() //用StdOut绘制该间隔 |
| public class Interval2D |
|---|
| Interval2D(Interval1D x, Interval1D y) //创建一个二维间隔 |
| double area() //二维间隔的面积 |
| boolean contains(Point2D p) //p是否在间隔中 |
| boolean intersect(Interval2D that) //两个间隔是否相交 |
| void draw() //用StdOut绘制该间隔 |
信息处理:
| public class Date implements Comparable |
|---|
| Date( int mont, int day, int year) //创建一个日期 |
| Date( String date) //创建一个日期(解析字符串的构造函数) |
| int month() //月 |
| int dayh() //日 |
| int year() //年 |
| String toString() //对象的字符串表示 |
| boolean equals(Object that) //该日期与that是否相同 |
| int compareTo( Date that) //日期与that比较 |
| int hashCode() //散列值 |
| public class Transaction implements Comparable |
|---|
| Tansaction( String who, Date when, double amount) |
| Tansaction( String transaction) |
| String who() //客户名 |
| Date when() //交易日期 |
| double amount() //交易金额 |
| String toString() //对象的字符串表示 |
| boolean equals(Object that) //该交易是否与taht相同 |
| int compareTo( Transaction that) //该交易与that比较 |
| int hashCode() //散列值 |
字符串:一个String值是一串可以由索引访问的char值。
为什么不使用字符数组代替Sting?地球上程序员答案都一样:为了使得代码更加简洁。
| public class String |
|---|
| String() //创建一个空字符串 |
| int length() //字符串长度 |
| int charAt(int i) //第i个字符 |
| int indexOf(String p) //p第一次出现的位置(若没有则返回-1) |
| int indexOf( string p, int j) //类似于C++中find |
| String concat(String t)//将t附在该字符串末尾,可用’+'代替 |
| String substring(int i, int j) //[i,j)子字符串 |
| String[] split(String delim) //使用delim分隔符切分字符串(支持正则表达式) |
| int compareTo(String t) //比较字符串 |
| boolean equals(String t) //比较与字符串t是否相同 |
| int hasCode() //散列值 |
输入输出:
| public class In //In也支持StdIn的所有错做 |
|---|
| In() //从标准输入创建输入流 |
| In(String name) //从文件或网站创建输入流 |
| boolean isEmpty() //如果输入流为空则返回true |
| int readInt() //读取一个int类型 |
| int readDouble() |
| void close() //关闭输入流 |
| public class Out //Out也支持StdOut的所有错做 |
|---|
| Out() //从标准输出创建输出流 |
| Out(String name) //从文件创建输出流 |
| void print(String s) //将s添加到输出流中 |
| void println(String s) //将s和一个换行符添加到输出流中 |
| void println(String s) //将s和一个换行符添加到输出流中 |
| void printf(String f,…) //格式化并打印输出流 |
| void close() //关闭输入流 |
| public class Draw //Draw也支持StdDraw所支持的所有操作 |
|---|
| Draw() |
| void line( double x0, double y0, double x1, double y1) |
| void point( double x, double y) |
Java中的类(class)实现抽象数据类型并将所有代码放入一个和类名相同并带有.java的扩展名的文件中。
文件的第一部分语句会定义表示数据类型的值的实例变量。
之后是实现对数据类型的值的操作的构造函数和实例方法。实例方法可以是公有的,也可以是私有的。
一个数据类型的定义中可能含有多个构造函数,而且也可能含有静态方法。
-
实例变量:要定义数据类型的值(即每个对象的状态),我们需要声明实例变量,生命的方式和局部变量类似,最关键的区别在于每一时刻每个局部变量只会有一个值,但是每个实例变量则对应无数值(数据类型的每个实例对象都会有一个)。在访问实例变量时,需要通过一个对象。同时,声明实例变量需要一个可见性修饰符。在抽象数据类型中,使用private进行修饰。
-
构造函数:每个Java类都至少含有一个构造函数来创建一个对象的标识。构造函数类似于静态方法,但它能够直接访问实例对象且没有返回值。一般而言,构造函数的作用是初始化实例变量。每个构造函数都将创建一个对象并向调用者返回一个该对象的引用。构造函数的名称与类名相同。且可以通过重载来定义多个标签不同的构造函数。若没有人为定义,类将会隐式地默认定一个不接受任何参数的构造函数并将所有实例变量初始化为默认值。
-
实例方法:与静态方法的代码相同。每一个实例方法都有一个返回值类型,一个签名(指明了方法名,所有参数变量的类型和名称)和一个主体(由一系列语句组成,包括一个返回语句来将一个返回类型的值传递给调用者)。实例方法与静态方法不同之处:前者可以访问并操作实例变量。那如何指定使用对象的实例变量?答案:在一个实例方法中对变量的引用指的是调用该方法的对象的值。
作用域:在Java代码中存在三种变量:参数变量、局部变量、实例变量。前两者与静态方法一样,在方法被调用时参数变量会被初始化为调用者提供的值;局部变量的声明和初始化都在方法的主体中。参数变量的作用域是整个方法;局部变量的作用域是当前代码段中它定义之后的所有语句。实例变量完全不同:它为该类的对象保存了数据类型的值,它的作用域是整个类。
- 抽象数据类型:一种向用例隐藏内部表示的数据类型。
- 封装:面向对象编程的一大特征。一个封装的数据类型可以被任意用例使用。
- 接口:编程语言为定义对象之间的关系提供的支持。
- 接口继承:实现类继承的是接口。例如:子类型,一种继承机制,允许程序员通过指定一个含有一组公共方法的的接口为两个本来没有关系的类建立一种联系,这两个类都必须实现这些方法。
- 实现继承:子类,又称为派生类,是另一种继承机制。它通过定义一个新类(即子类)来继承类一个类(即父类,又称为基类)的所有实例方法和实例变量。子类包含的方法比父类更多。另外,子类中可以重新定义或重写父类的方法。它被广泛用于编写可扩展的库。
- 封装类型:指Java提供的一些内置引用类型。每一种原始数据类型都有对应的封装类型。
- 等价关系:自反性、对称性、传递性、一致性、非空性。
- 垃圾回收:Java一个特性是自动内存管理。它通过记录孤儿对象并将它们的内存释放到内存池中,进而将程序员从管理内存的责任重解放出来。
- 不可变数据类型:指某种类型的对象的值创建之后无法被改变。Java通过final修饰符来强制不可变性。final保证变量只能被声明一次,可以用赋值语句,也可以用构造函数。不可变数据类型的缺点在于:1. 需要为每一个值创建一个新对象;2. 它只能保证原始数据类型的实例变量的不可变性,而无法用于引用类型的变量。(若引用类型为final声明的,则该引用只能指向同一个对象,但该对象的值本身可变。)
- 可变数据类型:使用可变数据类型时,必须时刻关注它们的值在何处发生变化。
- 异常(Exception):一般用于处理不被我们控制的不可预见的错误。例如StackOverflowError、ArithmeticaException、OutOfMemoryError、ArryIndexOutOfBoundsExceptio等。
- 断言(Assertion):验证代码中作出的一些假设。断言是一条需要在程序的某处确认为true的布尔表达式,如果表达式为false,程序将会终止并报告出一条错误信息。
-
为什么使用数据抽象?
答:数据抽象可以帮助程序员编写可靠且正确的代码。 -
为什么要区分原始数据类型和引用类型?为什么不单纯使用引用类型。
答:这主要是考虑性能因素。Java提供了Integer、Double等和原始数据类型对应的引用类型,以供希望忽略这些类型的区别的程序员使用。原始数据类型更接近计算机硬件支持的数据类型,因此比使用引用更快一些。 -
数据类型必须是抽象的吗?
答:未必。Java支持public和protected来帮助用例直接访问实体变量。 -
如果创建一个对象时忘记使用new关键字会发生什么?
答:发生错误。在Java中,new的使用看起来像使用一个静态方法,返回一个对象类型的返回值。 -
如果创建一个对象数组时忘记new会发生什么?
答:创建每一个对象都需要new,所以创建一个含有N个对象的数组,需要使用N+1次new。其中创建数组需要一次,创建每个对象各需要一次。 -
指针是什么?
答:指针可以看作机器地址。在Java中,创建引用的方法只有一种,即使用new关键字,且改变引用的方法也只有一种,即使用赋值语句。也就是说,程序员对于引用类型的操作只有创建和赋值。Java中的引用被称为安全指针。因为Java能够保证每个引用都会指向某个类型的对象。 -
import一个对象名意味着什么?
答:从某种意义上说,只是少打一些字。类似于Arrarys,如果不想使用import,可以使用java.util.Arrays. -
实现继承有什么问题?
答:子类继承阻碍模块化编程的原因有二。1. 父亲的任何改动都会影响到它所有的子类。子类的开发必然与父类有关。事实上,子类是完全依赖父类的。2. 子类代码可以访问所有实例变量,因此极有可能扭曲父类代码的意图。 -
如何才能使一个类不可变?
答:要保证一个可变类型的实例变量的数据类型的不可变性,需要得到一个本地副本,这被称为保护性复制。 -
什么是NULL?
答:NULL是一个不指向任何对象的字面量。引用null调用一个方法是没有意义的,并且会产生NullPointerException。 -
实现某种数据类型的类中能否存在静态方法?
答:可以。 -
除了参数变量、局部变量、实例变量之外还有其他种类的变量吗?
答:还有一种变量被称为静态变量。其使用方法是在类型之前添加关键字static. 和实例变量相同,类中的所有方法都可以访问静态变量,但是静态变量却不和任何具体的对象相关联。在较老的编程语言中,这种变量被称为全局变量,因为它们的作用域是全局的。在现代编程中,我们希望限制变量的作用域,因此很少使用这种变量。 -
什么是deprecated的方法?
答:deprecated 指的是不再被支持,但是为了保持兼容性而留在API中的方法。
1.3 背包、队列、栈
背包、队列、栈三种数据类型非常基础且应用广泛。它们之间的不同之处在于删除或者访问对象的顺序不同。
这里需要补充一点泛型的知识,泛型又称为参数化类型,例如在以下API中的Item,它并不是某种具体数据类型,但它可以来替换为任意类型的数据,Bag
另外,参数类型必须被实例化为引用类型。Java有一种特殊机制来使泛型代码能够处理原始数据类型。在处理赋值语句、方法的参数和算符或逻辑表达式时,Java会自动在引用类型和对应的原始数据类型之间进行转化。
-
自动装箱:自动将一个原始数据类型转换为一个封装类型。
-
自定拆箱:自动将一个封装类型转化为一个原始数据类型。
-
背包:一种不支持从其中删除元素的结合数据类型。它的目的是帮助用例手机元素并迭代遍历所有收集到的元素。
| public class Bag |
|---|
| Bag() //创建一个空背包 |
| void add(Item item) //添加一个元素 |
| boolean isEmpty() //背包是否为空 |
| int size() //背包中元素的数量 |
-
队列:又称为先进先出队列,一种基于先进先出(FIFO)策略的集合类型。队列最大的特点是可以保存了元素的相对顺序:其如对顺序和出队顺序相同。
|public class Queue- implements Iterable
- //队列的API|
|-|-|
|Queue() //创建一个空队列|
|void enqueue(Item item) //添加一个元素(入队)|
|Item dequeue() //删除最早添加的元素(出队)|
|boolean isEmpty() //队列是否为空|
|int size() //队列中元素的数量| - implements Iterable
-
下压栈:简称栈,一种基于后进先出(LIFO)策略的集合类型。它的特点在于元素的处理顺序和它们被压入栈的顺序正好相反。
|public class Stack- implements Iterable
- //栈的API|
|-|-|
|Stack() //创建一个空栈|
|void push(Item item) //添加一个元素(压栈)|
|Item pop() //删除最早添加的元素(出栈)|
|boolean isEmpty() //栈是否为空|
|int size() //栈中元素的数量| - implements Iterable
这里介绍一个栈的一个基本应用:中缀表达式转后缀表达式。
中缀转后缀的原理:对于一行表达式,从左到右依次读取,如果是操作数就将它输出.遇到操作符 A 就将它压入堆栈 (此时可以视 A 为栈顶元素) ,直到遇到下一个操作符 B ,如果操作符 B 比栈顶操作符 (A) 的优先级低(或者相同),则弹出 A ,反之则压入堆栈.
遇到括号时,把左括号压入堆栈中,并同时从左括号起视为一个新的堆栈.
举例:对于中缀表达式 a + b * c + ( d * e + f) * g,有以下步骤:
| 步骤 | 堆栈 | 输出 |
|---|---|---|
| 1 | a | |
| 2 | + | a |
| 3 | + | ab |
| 4 | +* | ab |
| 5 | +* | abc |
| 6 | + | abc*+ |
| 7 | + | abc*+ |
| 8 | +( | abc*+ |
| 9 | +( | abc*+d |
| 10 | +(* | abc*+de |
| 11 | +(+ | abc*+de*f |
| 12 | +(+ | abc*+de*f |
| 13 | +* | abc*+de*f+g |
| 14 | abc*+def+g+ |
- 定容栈:顾名思义,这是一种表示固定容量的字符串栈的抽象数据类型。与Stack不同,定容栈只能处理String值,且要求用例制定一个容量,且不能迭代访问。
| public class FixedCapacityStackOfStrings |
|---|
| FixedCapacityStackOfStrings(int cap) //创建一个容量为cap的定容栈 |
| void push(String item) //添加一个字符串(压栈) |
| String pop() //删除最早添加的字符串(出栈) |
| boolean isEmpty() //栈是否为空 |
| int size() //栈中元素的数量 |
定容栈API的实现:
public class FixedCapacityStackOfStrings {
private String[] a;//stack entries;
private int N;
public FixedCapacityStackOfStrings( int cap){
a = new String[ cap];
}
public boolean isEmpty(){
return N == 0;
}
public int size(){
return N;
}
public void push( String item){
a[N++] = item;
}
public String pop(){
return a[--N];
}
}
一个简单的例子:
import edu.princeton.cs.algs4.*;
public class Test {
public static void main( String[] args) {
FixedCapacityStackOfStrings s;
s = new FixedCapacityStackOfStrings(100);
while( !StdIn.isEmpty()){
String item = StdIn.readString();
if( !item.equals("-"))
s.push( item);
else if( !s.isEmpty())
StdOut.print( s.pop() + " ");
}
}
}
//在上例中,如果输入为"-"代表出栈,否则入栈。
//当输入为"to be or not to - be - - that - - - is"时,
//输出为"to be not that or be"
- 泛型:在上述例子中,FixedCapacityStackOfStrings 只能处理String对象。为了扩展其通用性,我们可以使用泛型。这里给出一种新的定容栈FixedCapacityStack,可以结合FixedCapacityStackOfStrings的API及实现来对比分析。
| public class FixedCapacityStack |
|---|
| FixedCapacityStack(int cap) //创建一个容量为cap的定容栈 |
| void push(Item item) //添加一个元素(压栈) |
| Item pop() //删除最早添加的元素(出栈) |
| boolean isEmpty() //栈是否为空 |
| int size() //栈中元素的数量 |
public class FixedCapacityStack {
private Item[] a;//stack entries;
private int N;
public FixedCapacityStackOfStrings( int cap){
a = (Item[]) new Object[cap];
}
public boolean isEmpty(){
return N == 0;
}
public int size(){
return N;
}
public void push( Item item){
a[N++] = item;
}
public Item pop(){
return a[--N];
}
}
如何改变定容栈的大小?在Java中,数组一旦创建,其大小是无法改变的。考虑两种情况,如果集合元素数量远小于数组大小,则会造成浪费;如果集合元素数量大于数组大小,则可能发生溢出。
综合以上观点,我们应该修改数组的实现,可以使用动态调整数组大小的方法来使得既可以保存所有元素,又不至于浪费太多空间。
具体实现:首先实现一个方法,可以将栈 a 移动到另外一个大小不同的数组中:
//将大小为N
private void resize( int max){
Item[] temp = (Item[]) new Object[ max];
for( int i = 0; i < N; i++)
temp[i] = a[i];
a = temp;
}
之后,在 push() 中,检查数组是否会发生一处。如果没有多余空间,则会将数组大小加倍,之后再使用 a[ N++] = item.
public void push( Item item){
if( N == a.length)
resize( 2 * a.length);
a[ N++] = item;
}
类似,在pop()中出栈,如果数组长度太大,则我们可以将它的长度减半。正确的检测条件:栈大小是否小于数组的四分之一。
public Item pop(){
Item item = a[--N];
a[N] = NULL; //避免对象游离
if( N > 0 && N == a.length / 4)
resize( a.length / 2);
return item;
}
在以上实现中,栈永远也不会发生一处,且使用率也不会低于四分之一。当然,存在例外情况,当栈为空时,数组大小为1.
- 对象游离:保存一个不需要的对象的引用。
例如,在之前的pop()实现中,被出栈的元素实际上依旧存在数组中,但此时该元素已经属于一个孤儿(即永远不会被访问)。避免对象游离很容易,可以将出栈位置的元素设为null即可。
- 迭代:用某种方式处理集合中的每一个元素。
例如:
for( int it : a){
//其中a的数据类型为 Stack以上代码形式称为foreach语句,这种形式既清晰又简洁,且不依赖与集合数据类型的具体实现。
任意可迭代的集合数据类型中需要实现的有:1. 集合数据类型必须是实现一个iterator())方法并返回一个Iterator对象;2. Iterator类必须包含两个方法,hasNext() 和 next(), 其中前者返回一个布尔值,后者返回一个泛型元素。
在Java中,我们使用接口机制来指定一个类所必须实现的方法。对于可迭代的集合数据类型,第一步需要在生命中加入implements Iterable,对应的接口为:
public interface Iterable- {
Iterator
- iteraotor();
}
然后在类中添加一个方法iterator() 并返回一个迭代器Iterator.迭代器都是泛型的,因此我们可以使用参数类型Item来帮助用例遍历他们指定的任意类型的对象。对于一直使用的数组表示法,我们需要逆序迭代遍历这个数组,因此我们将迭代器命名为 ReverseArrayIterator, 并添加了以下方法:
public Iterator- iterator(){
return new ReverseArrayIterator();
}
迭代器是实现了 hasNext() 和 next() 方法的类的对象,其接口定义为:
public interface Iterator- {
boolean hasNext();
Item next();
void remove();
//其中remove()方法为空,因为希望避免迭代中穿插能够修改数据结构的操作。
}
对于 ReverseArrayIterator, 这些方法只要一行代码,他们实现在栈类的一个嵌套类中:
import java.util.Iterator;
private class ReverseArrayIterator implements Iterator- {
private int i = N;
public boolean hasNext(){
return i > 0;
}
public Item next(){
return a[--i];
}
public void remove(){};
}
现在给出能够动态调整数组大小的下压栈的实现代码。它支持foreach语句按照后进先出的顺序迭代访问所有栈元素。
import java.util.Iterator;
public class ResizingArrayStack- implements Iterable
- {
private Item[] a = (Item[]) new Object[1];//栈元素
private int N = 0; //元素数量
public boolean isEmpty(){
return N == 0;
}
public int size(){
return N;
}
private void resize( int max){
Item[] temp = (Item[]) new Object[ max];
for( int i = 0; i < N; i++)
temp[i] = a[i];
a = temp;
}
public void push( Item item){
if( N == a.length)
resize( 2 * a.length);
a[ N++] = item;
}
public Item pop(){
Item item = a[--N];
a[N] = NULL; //避免对象游离
if( N > 0 && N == a.length / 4)
resize( a.length / 2);
return item;
}
}
public Iterator
- iterator(){
return new ReverseArrayIterator();
}
private class ReverseArrayIterator implements Iterator
- {
private int i = N;
public boolean hasNext(){
return i > 0;
}
public Item next(){
return a[--i];
}
public void remove(){};
}
虽然以上方法解决了很多问题,但是在理论上具有一定的缺陷:它无法达到最佳性能(每次操作用时都与集合大小无关;空间需求总是不超过集合大小乘以一个常数)。其问题的关键在于push() 和 pop() 操作会调整数组的大小,这些耗时与栈大小有关。
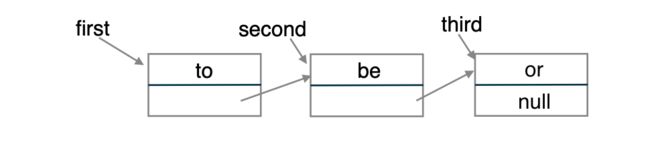
- 链表:链表是一种递归的数据结构,它或者为null,或者是指向一个结点的引用,该结点含有一个泛型的元素和一个指向另一条链表的引用。
//嵌套类定义结点的抽象数据类型
private class Node{
Item item;
Node next;
}
//可以通过new Node()来构造一个Node类型,并被初始化为null
现在,假设我们以一个例子介绍链表的基本操作。
//假设存在三个结点,first,second,third.
//首先创建三个结点
Node first = new Node();
Node second = new Node();
Node third = new Node();
//构造每个结点的item与next.
first.item = "to";
second.item = "be";
third.item = "or";
first.next = second;
second.next = third;
- 插入结点,插入结点可以细分为两类:在表头插入;在其他位置插入。
Node insert_head = new Node();
insert_head.item = "insert";
//在表头插入新结点
insert_head.next = first;
//在其他位置插入新结点
//首先假设某一点pre已经移动到待插入结点的前面
insert_head.next = pre.next;
pre.next = insert_head;
- 删除结点,同样可以分为两类:在表头删除;在其他位置删除。这里需要注意的一点,Java的内存管理系统可以自动回收它所占用的内存。而不用C++中的free 和 delete.
//在表头删除
first = first.next;
//其他位置处删除,例如删除second
first.next = third;
//其他位置处删除,例如删除尾部结点third
second.next = null;
- 遍历:遍历链表中所有元素的代码为:
for( Node x = first; x != null; x = x.next){
;//处理x.item
}
链表实现下压栈:链表的使用可以达到最优设计目标:1. 可以处理任意的数据类型;2. 所需要的空间与集合大小成正比;3. 操作所需要的时间与集合大小无关。
//链表实现下压栈
public class Stack- {
private Node first;
private int N;
private class Node{
Item item;
Node next;
}
public boolean isEmpty(){
return first == null;
}
public int size(){
return N;
}
public void push( Item item){
Node oldfirst = first;
first = new Node();
first.item = item;
first.next = oldfirst;
N++;
}
public Item pop(){
Item item = first.item;
first = first.next;
N--;
return item;
}
}
用链表实现先进先出队列:
//用链表实现先进先出队列
public class Queue- {
private Node first;
private Node last;
private int N;
private class Node{
Item item;
Node next;
}
public boolean isEmpty(){
return first == null;
}
public int size(){
return N;
}
public void enqueue( Item item){
Node oldlast = last;
last = new Node();
last.item = item;
last.next = null;
if( isEmpty())
first = last;
else
oldlast.next = last;
N++;
}
public Item dequeue(){
Item item = first.item;
first = first.next;
if( isEmpty())
last = null;
N--;
return item;
}
}
用链表实现背包:用链表实现背包,可以将Stack中的push()换成add(),同时去掉pop() 即可。
//用链表实现背包
public class Bag- implements Iterable
- {
private Node first;
private class Node{
Item item;
Node next;
}
public void add( Item item){
Node oldfirst = first;
first = new Node();
first.item = item;
first.next = oldfirst;
}
public Iterable
- iterator(){//简单实现了从实现Iterator接口的类中返回一个对象
return new ListIterator();
}
private class ListIterator implements Iterator
- {
private Node current = first;
public boolean hasNext(){
return current != null;
}
public void remove(){
}
public Item next(){
Item item = current.item;
current = current.next;
return item;
}
}
}
至此,我们了解了两种表示对象集合的方式:数组、链表。前者被称为顺序存储,后者被称为链式存储。
| 结构 | 优点 | 缺点 |
|---|---|---|
| 数组 | 索引访问,耗时O(1) | 初始化时需知元素数量 |
| 链表 | 耗费空间大小与元素数量成正比 | 引用访问,耗时O(N) |
-
并不是所有语言都支持泛型,甚至Java的早期版本也不支持。有解决办法吗?
答:方法一:对于每一种类型的数据实现一个不同的数据类型;方法二,构建一个 Object对象的栈,并在用例中使用pop()时将得到的对象转换为所需要的数据类型。 -
为什么Java中不允许泛型数组?
答:这个问题仍存在争论。 -
如何创建一个字符串栈的数组?
答:使用类型转换,例如:Stack[] t = (Stack []) new Stack[N]; -
栈为空时调用pop()会发生什么?
答:这取决于用什么实现。如果用数组实现,会出现越界;如果用链表实现,会得到NullPointerException 异常。 -
为什么将Node声明为嵌套类?为什么使用private?
答:将Node声明为私有的嵌套类之,我们可以讲Node的方法和实例变量的访问范围限制在包含它的类中。
私有嵌套类的一个特点是只有包含它的类才能直接访问它的实例变量。 -
Java标准库中有栈和队列吗?
答:Java又一个内置的库叫做java.util.Stack. 但是它包含几个不属于栈的方法,例如获取第i个元素,它还允许从栈底添加新的元素(类似于队列)。 -
如果使用 javac Stack.java 编译时,出现了两个文件,分别是Stack.class 和 Stack N o d e . c l a s s , 为 什 么 ? 答 : 第 二 个 文 件 是 内 部 类 N o d e 创 建 的 ( 内 部 类 : 非 静 态 的 嵌 套 类 ) 。 J a v a 的 命 名 规 则 会 使 用 Node.class,为什么? 答:第二个文件是内部类Node创建的(内部类:非静态的嵌套类)。Java的命名规则会使用 Node.class,为什么?答:第二个文件是内部类Node创建的(内部类:非静态的嵌套类)。Java的命名规则会使用分割外部类和内部类。
-
是否允许向栈或队列中添加 null元素(空元素)?
答:允许。 -
在Stack中,如果在迭代过程中调用push()或pop(), 其迭代器会怎么做?
答:抛出 java.util.ConcurrentModeificationException 的异常。 -
我们可以使用foreach 循环访问数组吗?
答:可以。(尽管数组没有实现Iterable接口) -
我们可以使用foreach 循环访问字符串吗?
答:不可以。(String 没有实现Iterable接口)
1.4 算法分析
准确测量给定程序的确切时间是十分困难的。不过好在我们只需要近似值即可。
可以使用一种计时器的思想。使用如下数据类型:
| public class Stopwatch //一种表示计时器的抽象数据类型 |
|---|
| Stopwatch() //创建计时器 |
| double elapseTime() //返回对象创建以来所经过的时间 |
其数据类型的实现为:
public class Stopwatch{
private final long start;
public Stopwatch(){
start = System.currentTimeMillis();
}
public double elapsedTime(){
long now = System.currentTimeMillis();
return (now - start) / 1000.0;
}
}
享誉全球的计算机科学家 Knuth 认为,虽然有许多因素影响程序的运行时间,但是原则上我们仍然可以构造出一个数学模型来描述任意程序的运行时间。他认为,一个程序运行时间于两部分有关:1. 执行每条语句的耗时;2. 执行每条语句的频率。前者取决于计算机硬件与软件,后者取决于程序本身。
以下述程序为例:
public static int count( int[] a){
int N = a.length;
int cnt = 0;
for( int i = 0 ; i < N; i++)
for( int j = i + 1; j < N; j++)
for( int k = j + 1; k < N; k++)
if( a[i] + a[j] + a[k] == 0)
cnt++;
return cnt;
}
在以上程序中,条件语句执行 N(N-1)(N-2)/6 次,展开后为 N 3 6 − N 2 2 + N 3 \frac{N^3}{6} - \frac{N^2}{2} + \frac{N}{3} 6N3−2N2+3N
假设 N = 1000, 代入可得 N^3/6 = 166666667, 而 -N^2/2+N/3 = 499667. 相比与首项,其余项相对较小,因此我们可以用符号 ‘~’ 来表示近似,忽略较小的项,进而极大简化数学公式。
- ~f(N): 表示随着N的增大除以f(N)的结果趋于1的函数。
- g(N) ~ f(N):表示 g(N)/f(N) 随着N的增大趋近于1. 一般近似方式为g(N) ~ af(N), 将f(N) 称为g(N)的增长的数量级。
例如:
| 函数 | 近似 | 增长的数量级 |
|---|---|---|
| N 3 6 − N 2 2 + N 3 \frac{N^3}{6} - \frac{N^2}{2} + \frac{N}{3} 6N3−2N2+3N | ~ N 3 6 \frac{N^3}{6} 6N3 | N 3 N^3 N3 |
| N 2 2 − N 3 \frac{N^2}{2} - \frac{N}{3} 2N2−3N | ~ N 2 2 \frac{N^2}{2} 2N2 | N 2 N^2 N2 |
| l g N + 1 lgN + 1 lgN+1 | ~ l g N lgN lgN | l g N lgN lgN |
| 3 | ~3 | 1 |
另外,这里给出常见的增长数量及函数:
| 描述 | 函数 | 举例 |
|---|---|---|
| 常数级别 | 1 1 1 | 两数相加 |
| 对数级别 | l o g N logN logN | 二分查找 |
| 线性级别 | N N N | 遍历数组 |
| 线性对数级别 | N l o g N NlogN NlogN | 快速排序 |
| 平方级别 | N 2 N^2 N2 | 双层循环 |
| 立方级别 | N 3 N^3 N3 | 三层循环 |
| 指数级别 | 2 N 2^N 2N | 枚举,例检查所有子集 |
考虑一个十分重要的命题:许多程序的运行时间只是取决于其中的一小部分指令。执行最频繁的指令决定了程序执行的时间。
在count代码中,运行时间主要取决于三个循环语句,而不是条件判断语句。因此它的运行时间为 a N 3 ~aN^3 aN3,其中a为取决于计算机硬件的某个具体常数。
对于大多数程序,得到其运行时间的数学模型所需步骤如下:1. 确定输入模型,定义问题的规模;2. 识别内循环;3.根据内循环中的操作确定成本模型;4. 对于给定输入,判断这些操作的执行频率。
算法分析中常见函数:
| 描述 | 记号 | 定义 |
|---|---|---|
| 向下取整(floor) | ⌊ x ⌋ \lfloor x \rfloor ⌊x⌋ | 不大于x的最大整数 |
| 向上取整(ceil) | ⌈ x ⌉ \lceil x \rceil ⌈x⌉ | 不小于x的最小整数 |
| 自然对数 | l n N lnN lnN | l o g e N log_e N logeN |
| 以2为底的对数 | l g N lgN lgN | l o g 2 N log_2 N log2N |
| 以2为底的整型对数 | ⌊ l g N ⌋ \lfloor lgN \rfloor ⌊lgN⌋ | 不大于 l o g 2 N log_2 N log2N的最大整数 |
| 调和级数 | H N H_N HN | 1 + 1/2 + 1/3 +…+1/N |
| 阶乘 | N ! N! N! | 123*…*N |
算法分析中常见的近似函数
| 描述 | 近似函数 |
|---|---|
| 调和级数求和 | H N ∼ l n N H_N \sim lnN HN∼lnN |
| 等差数列求和 | ∑ i = 1 N i ∼ N 2 / 2 \sum_{i=1}^{N}{i} \sim N^2/2 ∑i=1Ni∼N2/2 |
| 等比数列求和 | ∑ i = 1 N 2 i ∼ 2 N \sum_{i=1}^{N}{2^i} \sim 2^N ∑i=1N2i∼2N |
| 斯特灵公式 | l g N ! ∼ N l g N lgN! \sim NlgN lgN!∼NlgN |
| 二项式系数 | C N k ∼ N k / k ! C_N^k \sim N^k/k! CNk∼Nk/k! |
| 指数函数 | ( 1 − 1 / x ) x ∼ 1 / e (1-1/x)^x \sim 1/e (1−1/x)x∼1/e |
- 均摊分析:记录所有操作的总成本并除以操作综述来讲成本均摊。
例如:在基于可调整大小的数组实现的Stack数据结构中,对空数据结构进行的任意操作序列对数组的平均访问次数在最坏情况下均为常数。
原始数据类型的常见内存、需求:
| 类型 | 字节 |
|---|---|
| boolean | 1 |
| byte | 1 |
| char | 2 |
| int | 4 |
| float | 4 |
| long | 8 |
| double | 8 |
对象的内存开销 = 所用到的实例变量的内存开销 + 对象本身开销(16字节)+ 填充开销。
- 倍率实验:一种简单有效地预测任意程序的性能并判断他们的运行时间大致的增长数量级。
步骤:1. 开发一个输入生成器来产生实际情况下的各种输入。2. 运行输入生成器,并计算每次实验和上一次实验运行时间的比值。3. 反复运行知道该比值趋近于极限 2^b.
结论:1. 它们的运行时间的增长数量级约为N^b. 2. 要预测一个程序的运行时间,将上次观察得到的运行时间乘 2^b 并将N加倍,如此反复。
1.5 案例分析:union-find 算法
-
等价关系:一种等价关系,则它意味着:1. 自反性:p与p本身是等价的;2. 对称性:p与q等价,则q与p等价;3. 传递性:p与q等价,q与r等价,则p与r等价。
-
等价类:当且仅当两个对象等价时它们才属于同一个等价类。
问题概述:输入是一列的整数对,其中每一个整数都表示一个某种类型的对象,一对整数 “p - q” 可以理解为“p与q是相连的”。假设“相连”是一种等价关系。
目标:编写一个程序来过滤掉序列中所有无意义的整数对(两个整数均来自同一个等价类中). 简而言之,即若输入整数对 p-q, 若不能说明p-q是相连的,则将该整数对写入到程序中,否则忽略p-q.
例如: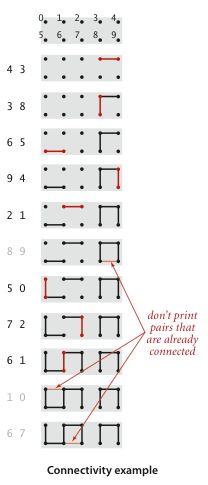
解决思路:将输入的所有整数看作不同的数学集合。在处理一个整数对 p-q 时,需要判断它们是否处于相同的集合。如果不是,则将p所属的集合和q所属的集合归并到同一个集合。
为方便,将对象称为触点,将整数对称为连接,将等价类称为连通分量(简称为分量)。
首先,设计一份API来封装所需要的基本操作:初始化、连接两个触点、判断两个触点是否存在与同一个分量之中、返回所有分量的数量、判断包含某一个触点的分量。
| public class UF |
|---|
| UF( int N) //以整数标识( 0 到 N - 1)初始化N个触点 |
| void union( int p, int q) //在p和q之间添加一条连接 |
| int find( int p) //查找p( 0 到 N - 1)所在的分量的标识符 |
| int count() //连通分量的数量 |
| boolean connected(int p, int q) //判断p和q是否存在于同一个分量中 |
这里,我们讨论三种不同的实现。它们均根据以触点为索引的id[]数组来确定两个触点是否存在相同的连通分量中。
三种方法只有 find 与 unoin 的实现不同。
方法一:quick-find算法:这种方法保证当且仅当 id[p] 与 id[q] 相等时 p 与 q 是联通的。
connected(p,q) 只需要判断 id[p] == id[q]. 当p与q在同一个联通分量中返回true.
union(p,q) 首先检查connected(p,q), 如果为true,则不操作;否则需要将p所在的id[] 与 q 所在的id[] 合二为一。为了实现合二为一,我们需要遍历整个数组,将所有和id[p] 相等的元素的值变为id[q]的值。(同样可以将所有与id[q]相等的元素值变为id[p]的值)
代码实现如下:
public class Unoin_Find {
// 高效的实现方法是前提
// 触点和分量都使用int类型表示
private int[] id; //分量id(以触点作为索引)
private int count; //分量数量
public UF( int N){ //初始化分量id数组
count = N;
id = new int[N];
for( int i = 0; i < N; i++)
id[i] = i;
}
public int count(){
return count;
}
public boolean connected( int p, int q){
return find( p) == find( q);
}
public int find( int p){
return id[p];
}
public void union( int p, int q){
int pID = find( p);
int qID = find( q);
if( pID == qID)
return ;
for( int i = 0; i < id.length; i++)
if( id[i] == pID)
id[i] = qID;
count--;
}
public static void main( String[] args){
int N = StdIn.readInt();
Unoin_Find uf = new Unoin_Find( N);
while( !StdIn.isEmpty()){
int p = StdIn.readInt();
int q = StdIn.readInt();
if( uf.connected())
continue;
uf.union( p, q);
StdOut.println( p + "-" + q);
}
StdOut.println( uf.count() + "components");
}
}
算法分析:find()操作运行时间为O(1), 但是union() 需要扫描整个id[]数组。 quick-find算法的运行时间为O(N^2).并不适合大规模运算。
方法二:quick-union算法:该算法与quick-find算法是互补的,它们基于相同的数据结构:以触点作为索引的id[]数组。但是在这两个算法中,数组元素的值的意义是不同的。
-
链接:每个触点所对应的id[]元素都是同一个分量中的另一个触点的名称(也可能是它自己)。
find():从给定的触点开始,由它的链接得到另外一个触点,然后再由这个触点链接到第三个触点,如此继续,知道到达一个根触点(根触点的链接指向本身,注意,根触点必然存在)。当且仅当两个触点的根触点相同时,这一对触点处于同一个联通分量。
union(p,q):由p和q的链接分别找到二者的根触点,之后将其中一个根触点链接到另一个既可。
代码:
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class Unoin_Find {
// 高效的实现方法是前提
// 触点和分量都使用int类型表示
private int[] id; //分量id(以触点作为索引)
private int count; //分量数量
public UF( int N){ //初始化分量id数组
count = N;
id = new int[N];
for( int i = 0; i < N; i++)
id[i] = i;
}
public int count(){
return count;
}
public boolean connected( int p, int q){
return find( p) == find( q);
}
public int find( int p){
while( p != id[p])
p = id[p];
return p;
}
public void union( int p, int q){
int pRoot = find( p);
int qRoot = find( q);
if( pRoot == qRoot)
return ;
id[ pRoot] = qRoot;
count--;
}
public static void main( String[] args){
int N = StdIn.readInt();
Unoin_Find uf = new Unoin_Find( N);
while( !StdIn.isEmpty()){
int p = StdIn.readInt();
int q = StdIn.readInt();
if( uf.connected())
continue;
uf.union( p, q);
StdOut.println( p + "-" + q);
}
StdOut.println( uf.count() + "components");
}
}
举例:注意,在quick-union算法中,用树表示更加直观,事实上,构造树并不困难。
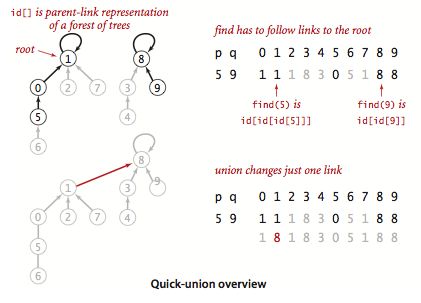
quick-union算法分析:最坏情况下,考虑N个触点,输入有序的0-1,1-2,2-3等,N-1对之后N个触点将全部处于相同的集合中,此时树的高度为N-1,其中0链接到1,1链接到2,2连接到3…因此处理如上所属的N对整数的所有find()操作的运行次数为2(1+2+3+…+N). 因此运行时间最坏情况下为O(N^2)。
方法三:加权quick-union算法: 为了防止出现上述最糟糕的情况,在union()的过程中,我们会记录每一棵树的大小并总是将较小的树连接到较大的树上。这项改动需要在原有的基础上添加一个数组来记录树中的结点数。
代码如下:
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class Unoin_Find {
// 高效的实现方法是前提
// 触点和分量都使用int类型表示
private int[] id; //分量id(以触点作为索引)
private int[] sz;
private int count; //分量数量
public UF( int N){ //初始化分量id数组
count = N;
id = new int[N];
for( int i = 0; i < N; i++)
id[i] = i;
sz = new int[N];
for( int i = 0; i < N; i++)
sz[i] = 1;
}
public int count(){
return count;
}
public boolean connected( int p, int q){
return find( p) == find( q);
}
public int find( int p){
while( p != id[p])
p = id[p];
return p;
}
public void union( int p, int q){
int pRoot = find( p);
int qRoot = find( q);
if( pRoot == qRoot)
return ;
if( sz[pRoot] < sz[qRoot]){
id[ pRoot] = qRoot;
sz[ qRoot] += sz[pRoot];
}
else{
id[ qRoot] = pRoot;
sz[ pRoot] += sz[qRoot];
}
count--;
}
public static void main( String[] args){
int N = StdIn.readInt();
Unoin_Find uf = new Unoin_Find( N);
while( !StdIn.isEmpty()){
int p = StdIn.readInt();
int q = StdIn.readInt();
if( uf.connected())
continue;
uf.union( p, q);
StdOut.println( p + "-" + q);
}
StdOut.println( uf.count() + "components");
}
}
方法四:最优算法:路径压缩。在理想情况下,我们希望每一个结点都能直接连接到它的根结点上,但我们又不希望像quick-find算法那样修改大量的链接。路径压缩中,可以在检查结点的同时将它们直接链接到根结点。
find():为了实现路径压缩,需要在find()操作中增加一个循环,将在路径上所有结点都直接链接到根结点,最终得到一颗几乎扁平化的树。
各种union-find算法的性能特点(最坏情况下):
| 算法 | 构造函数 | union() | find() |
|---|---|---|---|
| quick-find | N | N | 1 |
| quick-union | N | 树高 | 树高 |
| 加权quick-union | N | lgN | lgN |
| 使用路径压缩的quick-union | N | 非常接近1 | 非常接近1 |
| 理想情况 | N | 1 |
我的微信公众号
![]() -
-