统计思维(实例11)——时间序列分析
时间序列(time series)是来自随时间变化的系统的一系列度量。
本章使用的示例来自Zachary M. Jones。Jones的研究目的是调查像大麻合法化这样的政策性决定会对市场产生何种影响。希望大家对本章内容感兴趣,但借此机会重申对数据分析保持专业性态度的重要性。药品是否非法,哪些药品应当属于非法,这是很重要而又难以回答的公共政策问题,人们应当基于诚实准确的数据进行决策。
导入和清洗数据
从Jones先生的网站下载数据,通过下面代码将数据读取到一个pandas DataFrame中:
transactions = pandas.read_csv('mj-clean.csv', parse_dates=[5])这个DataFrame中每一行都代表一次交易,具有如下列:
- city 字符串,代表城市名
- state 州名的两字母缩写
- price 交易价格,单位为美元
- amount 购买量,单位为克
- quality 由购买者汇报的货品质量,值为高、中或低
- date 汇报日期,这个日期应该在购买日期后不久
- ppg 每克价格,单位为美元
- lat 交易发生地点的大致维度,由城市名获得
- lon 交易发生地点的大致经度
每次交易都是一个时间事件,因此这个数据集可以看成一个事件序列。很多分析时间序列的方法要求度量是均匀分布的,或者度量均匀分布至少可以使分析更为简单。
为了演示这些方法,将这个数据集按照汇报的质量分组,并计算每克的日均价格,将每组数据转换为均匀分布的序列。
def GroupByQualityAndDay(transactions):
groups = transactions.groupby('quality')
dailies = {}
for name, group in groups:
dailies[name] = GroupByDay(group)
return dailies
def GroupByDay(transactions, func=np.mean):
grouped = transactions[['date', 'ppg']].groupby('date')
daily = grouped.aggregate(func)
daily['date'] = daily.index
start = daily.date[0]
one_year = np.timedelta64(1, 'Y')
daily['years'] = (daily.date - start) / one_year
return dailygroupby是DataFrame的方法,返回一个GroupBy对象groups。得到的grouped是一个映射,将每个日期对应到包含该日期汇报价格的DataFrame。aggregate是GroupBy的方法,遍历所有的组,对组中每列都执行一个函数。GroupByDay方法得到的DataFrame包含列ppg、date和years。
绘制图形
GroupByQualityAndDay得到的结果是从每个质量级别到日均价格DataFrame的映射。绘制这3个时间序列的代码如下:
thinkplot.PrePlot(rows=3)
for i, (name, daily) in enumerate(dailies.items()):
thinkplot.SubPlot(i+1)
title = 'price per gram ($)' if i==0 else ''
thinkplot.Config(ylim=[0, 20], title=title)
thinkplot.Scatter(daily.index, daily.ppg, s=10, label=name)
if i==2:
pyplot.xticks(rotation=30)
else:
thinkplot.Config(xticks=[])具体绘制图形如下: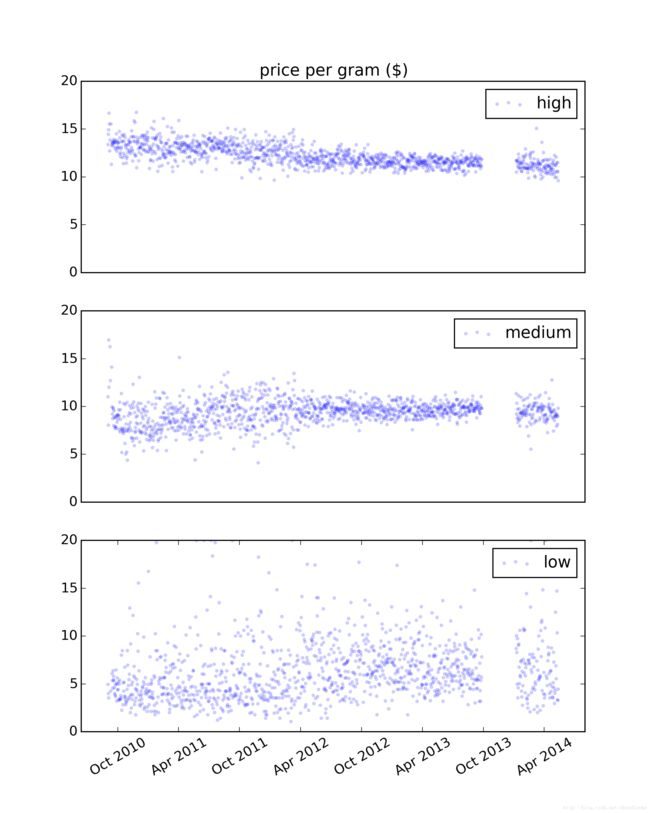
图1 高、中、低质量大麻的每克每日价格时间序列
从图中可以看到,这段时间内,高质量大麻价格似乎在降低;中等质量大麻价格在提高;低质量大麻的价格也在提高,但其价格变化过大,很难判断趋势。大麻质量的数据是由志愿者提供的,因此,这些随时间变化的趋势可能反映了参与者判断标准的变化。
线性回归
虽然时间序列分析有专门的方法,但对于很多问题,简单的方法是使用通用的工具,如线性回归。下面的函数以每日价格的DataFrame为参数,计算一个最小二乘法拟合,返回使用StatsModels包得到的模型和结果对象。然后,遍历dailies中的DataFrame,为每个DataFrame拟合模型。
def RunLinearModel(daily):
model = smf.ols('ppg ~ years', data=daily)
results = model.fit()
return model, results
for name, daily in dailies.items():
model, results = RunLinearModel(daily)
print(name)
regression.SummerizeResults(results)结果如下:
| 质量 | 截距 | 斜率 | R^2 |
|---|---|---|---|
| 高 | 13.450 | -0.708 | 0.444 |
| 中 | 8.879 | 0.283 | 0.050 |
| 低 | 5.362 | 0.568 | 0.030 |
估计所得斜率说明,在观测区间内,高质量大麻的价格每年下降约71%;中等质量大麻的价格每年上涨约28%;低质量大麻价格每年上涨57%。这些估计值都是统计显著的,p值很小。
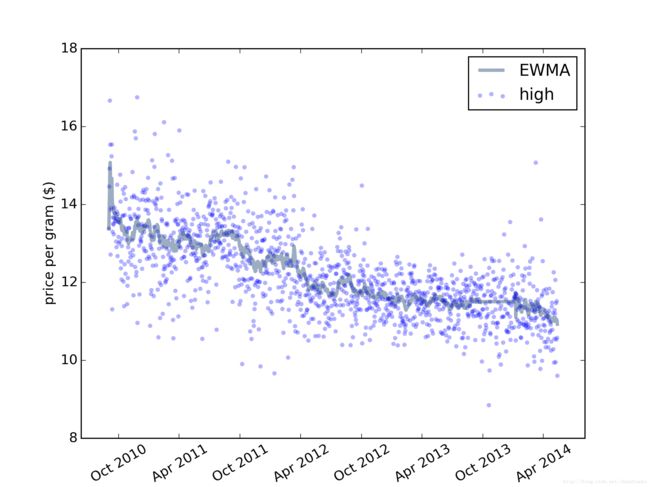
下图绘制高质量大麻数据点的散点图及拟合值的线图。
图2 高质量大麻每克每日价格的时间序列及线性最小二乘法拟合
图中模型似乎很好地拟合了数据,然而,线性回归并不是拟合这种数据的最适宜方法,原因如下:
- 预期长期趋势为线性的或符合其他简单函数,这是没有依据的。通常,价格由供需关系决定,而供给和需求都会随着时间发生不可预期的变化。
- 线性回归模型对所有数据使用通用的权重,不管是过去的还是近期数据。在进行预测是,近期数据也许应该得到更多的权重。
- 线性回归假设残差是无关的噪音。而在时间序列数据中,相邻数据是相关的,这项假设通常不能成立。
移动平均值
大部分时间序列分析基于的模型假设都认为,观察序列是三部分的总和:
- 趋势 描述持续变化的一个平滑函数
- 季节性 周期性的变化,可能包括每日、每周、每月或每年周期
- 噪音 长期趋势周围的随机变化
回归是从一个序列中获取趋势的方法。但是,如果这个趋势不是一个简单函数,那么一个很好的方法是移动平均值(moving average)。移动平均值将序列分为相互重叠的区域(称为窗口),计算每个窗口的平均值。
最简单的移动平均值是滚动均值(rolling mean),滚动均值计算每个窗口中值的均值。pandas提供rolling_mean方法,参数为Series和窗口大小,返回一个新的Series。
在对大麻数据使用rolling_mean方法之前,必须首先处理缺失数据。目前使用的DataFrame缺失这些数据,索引跳过了没有数据的日期。为了随后的分析,需要明确标明这些缺失的数据,为此,可以对DataFrame进行“重建索引”。
下面代码进行索引重建和滚动均值的绘制。
dates = pandas.date_range(daily.index.minx(), daily.index.max())
reindexed = daily.reindex(dates)
roll_mean = pandas.rolling_mean(reindexed.ppg, 30)
thinkplot.Plot(roll_mean.index, roll_mean)另一种移动平均值是指数权重移动平均(exponentially-weighted moving average, EWMA)。它有两个优点:指数权重移动平均计算加权平均值,最近的值具有最高的权重;pandas的EWMA实现可以较好地处理缺失值。
下图展示了两种平均值计算的效果:
图3 每日价格、滚动均值(左)和指数权重移动均值(右)
缺失值
填充缺失数据,一个简单的方法是使用移动平均值。Series的方法fillna就实现了这一功能。这一方法的缺点是弱化了序列中的噪音,这一问题可以通过添加重抽样的残差解决。
resid = (reindexed.ppg - ewma).dropna()
fake_data = ewma + Resample(resid, len(reindexed))
reindexed.ppg.fillna(fake_data, inplace=True)resid包含残差,但不包含ppg为nan的日期。fake_data包含移动平均值的结果与残差的一个随机样本的和。最后,fillna将nan替换为fake_data中的值。
序列相关
随着价格每日变化,你可能会期望看到一些模式。如果周一价格很高,可能随后几天都会较高;如果价格很低,可能会保持低位。在这种模式中,每个值都与序列中的下一个值相关,因此称为序列相关(serial correlation)。
要计算序列相关,我们可以将时间序列移动一个称为滞后(lag)间隔,然后计算移动后的序列与原序列的相关性。
def SerialCorr(series, lag=1):
xs = series[lag:]
ys = series.shift(lag)[lag:]
corr = Corr(xs, ys)
return corr使用不同的滞后值,可以检验序列的每周、每月和每年的季节性特征,具体结果如下:
| 滞后 | 高质量 | 中等质量 | 低质量 |
|---|---|---|---|
| 1 | -0.029 | -0.014 | 0.034 |
| 7 | 0.02 | -0.042 | -0.0097 |
| 30 | 0.014 | -0.0064 | -0.013 |
| 365 | 0.045 | 0.015 | 0.033 |
下一节将检验这些相关是否统计显著(结果不是),目前暂时认为,这些序列没有显著的季节性模式,至少在使用上述滞后值时没有。
自相关
自相关函数(autocorrelaton funciton)将滞后值映射到使用该值得到的序列相关。“自相关”是序列相关的另一个名字,常用于滞后值不为1时。
StatsModels软件包提供了时间序列分析函数,其中有计算自相关函数的acf。acf使用从0到nlags的滞后值计算序列相关。参数unbiased为True,告诉acf要为样本规模校正估计值。
如果选择高质量大麻的每日价格,抽取滞后为1、7、30和365的相关值,可以验证acf和SerialCorr得到的结果大致相同。
import statsmodels.tsa.stattools as smtsa
acf = smtsa.acf(filled.resid, nlags=365, unbiased=True)
acf[0], acf[1], acf[7], acf[30], acf[365]
1.000, -0.029, 0.020, 0.014, 0.044下图(左)展示了nlags=40时,3种质量分类的自相关函数。图中的灰色区域是不存在自相关是的正态可变性,位于这个区域之外的都是统计显著的。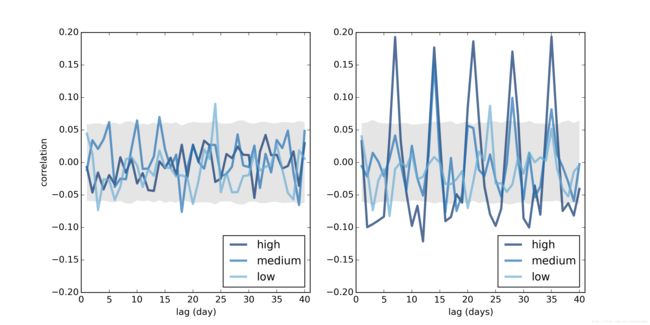
图5 每日价格的自相关函数(左)及模拟的每周季节性的每日价格(右)
为了展示存在季节性因素的自相关函数,在数据中加入一个每周的循环进行模拟。假设在周末是大麻的需求量较大,那么价格可能会较高。为了模拟这个效果,选择周五或周六的日期,在价格上添加一个随机量,这个随机量选自从0~2美分的均匀分布。
上图(右)展示出添加了模拟季节性的价格自相关函数。如我们所预期的,当滞后为7的倍数时,相关性较高。对于高质量和中等质量大麻,新得到的相关是统计显著的。而低质量大麻则不然,因为这一分类的残差最大,必须使用更大的模拟值。
预测
前面提到的线性回归可以用于预测,RegressionResults类提供predic方法,以包含解释变量的DataFrame为参数,返回一个预测序列。如果我们希望得到的只是单一的、最佳推测预测,那么predict就可以满足需求。但大部分时候需要对误差进行量化,即希望得知预测结果的准确性如何。
我们需要考虑三种误差来源:
- 抽样误差 预测基于估计参数,而估计参数依赖样本中的随机变异。
- 随机变异 即使估计参数是完美的,观测数据也会在长期趋势附近随机变动。
- 建模误差
另一种误差来源于无法预期的未来事件。农产品价格受天气影响,所有价格都会受政策和法律影响。
建模误差和无法预期的未来事件很难量化,而抽样误差和随机变异较容易处理,因此我们先处理后两种误差。
我们依然使用重抽样方法对抽样误差进行量化,重抽样的目的是使用实际观测来模拟重复进行实验时可能得到的数据。这种模拟基于的假设是,估计参数是正确的,但随机残差可能会不同。实现这种模拟的函数如下:
def SimulateResults(daily, iters=101):
model, results = RunLinearModel(daily)
fake = daily.copy()
result_seq = []
for i in range(iters):
fake.pgg = results.fittedvalues + Resample(results.resid)
_, fake_results = RunLinearModel(fake)
result_seq.append(fake_results)
return result_seq在每次循环中,代码对残差进行重抽样,将其附加在拟合值上,生成一个“伪”数据集,然后对伪数据拟合一个线性模型,将结果存储在RegressionResults对象中。
下一步是使用模拟结果生成预测:
def GeneragePredictions(result_seq, years, add_resid=False):
n = len(years)
d = dict(Intercept=np.ones(n), years=years, years2=years**2)
predict_df = pandas.DataFrame(d)
predict_seq = []
for fake_results in result_seq:
predict = fake_results.predict(predict_df)
if add_resid:
predict += Resample(fake_results.resid, n)
predict_seq.append(predict)
return predict_seq最后一步是绘制预测结果的90%置信区间,下图展示代码运行结果。图中深灰色区域代表取样误差的90%置信区间,即由取样导致的估计斜率和截距不确定性。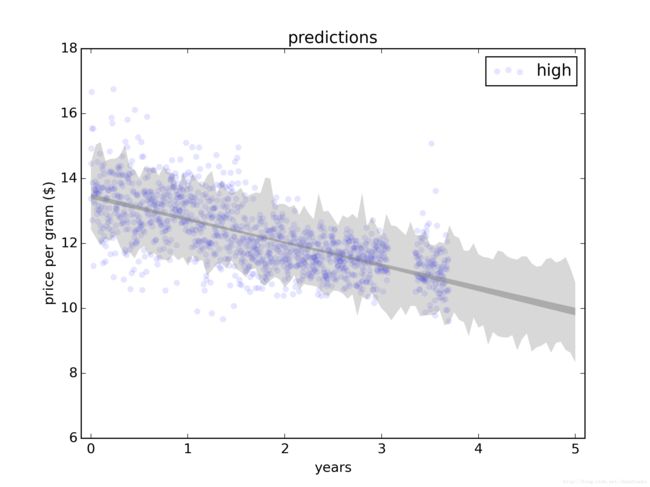
图6 基于线性拟合的预测,展示了由抽样误差和预测误差导致的变异
回归模型基于的假设是,系统是平稳的(stationary),即模型参数不会随着时间发生变化。具体来说,回归模型假设模型的斜率和截距是常数,残差分布也不变。
但前面的移动平均值图中,斜率在观测区间中似乎至少变化了一次,而且前半部分的残差方差似乎也比后半部分大。因此,我们得到的参数依赖观测区间。为了检验这一现象对预测结果的影响,我们可以对SimulateResult进行扩展,使用具有不同开始和结束日期的观测区间进行拟合。
下图展示了中等质量分类的预测结果。图中浅灰色区域代表各种误差的置信区间,包括取样误差、随机变异和观测区间变化。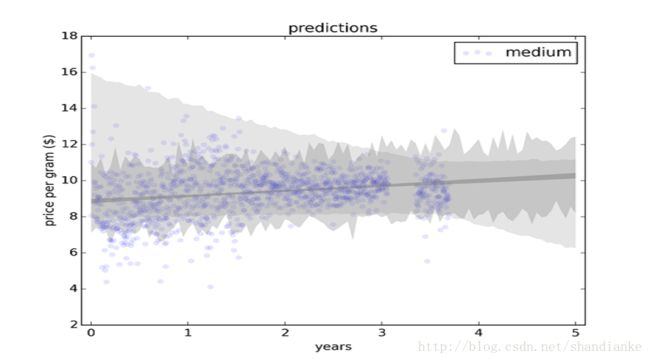
图7 基于线性拟合的预测,展示了由观测间隔导致的变异
基于整个区间的模型的斜率为正数,说明价格在上涨。而最近的区间显示出价格有下跌迹象,因此基于最近数据的模型斜率为负数。
参考文献:
统计思维. Allen B.Downey. 金迎 译