An Introduction on Deep Learning for the Physical Layer
An Introduction on Deep Learning for the Physical Layer
代码实现:https://github.com/shengjian3476077/DLforPhy
一、文章的主要工作
1、将通信系统设计视为端到端的重构任务,使用自编码器(autoencoder)实现端到端的通信系统,并在单个过程中共同优化发送器和接收器组件。
2、将上述系统扩展到多发射机和多接受机网络,
3、提出radio transformer networks(RTN),作为将专家领域知识纳入机器学习(ML)模型的手段。
4、使用CNN对IQ采样数据进行调制类型分类
二、自编码器

图中,虚线蓝色框内就是一个自编码器模型,它由编码器(Encoder)和解码器(Decoder)两部分组成,本质上都是对输入信号做某种变换。编码器将输入信号 x x x变换成编码信号 y y y,而解码器将编码 y y y转换成输出信号 x ~ \widetilde{x} x ,即 y = f ( x ) \mathrm{y}=f(x) y=f(x), x ~ = g ( y ) = g ( f ( x ) ) \widetilde{x}=g(\mathrm{y})=g(f(x)) x =g(y)=g(f(x))。而自编码器的目的是,让输出 x ~ \widetilde{x} x 尽可能复现输入 x x x,即tries to copy its input to its output。但是,这样问题就来了——如果 f f f和 g g g都是恒等映射,那不就恒有 x ~ = x \widetilde{x}=x x =x了么?因此,我们经常对中间信号 y \mathrm{y} y(也叫作“编码”)做一定的约束,这样,系统往往能学出很有趣的编码变换 f f f和编码 y \mathrm{y} y。对于自编码器,我们往往并不关系输出什么(反正只是复现输入),我们真正关心的是中间层的编码,或者说是从输入到编码的映射。可以这么想,在我们强迫编码 y y y和输入 x x x不同的情况下,系统还能够去复原原始信号 x x x,那么说明编码 y \mathrm{y} y已经承载了原始数据的所有信息,但以一种不同的形式!这就是特征提取啊,而且是自动学出来的!实际上,自动学习原始数据的特征表达也是神经网络和深度学习的核心目的之一。而自编码器的这种在深度学习中略显鸡肋的功能却在通信系统中占据了得天独厚的优势,我们可以把我们的通信系统的发射端看成Encoder,将接收端看成Decoder,而在信道中传输的便是经由Encoder学习到的 f f f映射后得到的编码信号 y \mathrm{y} y。
三、autoencoder实现单发射端、单接收端通讯系统
1、信道模型

发射端通过n个离散的信道发送M个可能的信息之一 s ∈ M = { 1 , 2 , … , M } \mathcal{s}\in\mathcal{M}=\{1,2,…,M\} s∈M={1,2,…,M}给接收端。可以认为,发射端即将转换 f : M → R n f:\mathcal{M}\to\mathbb{R}^n f:M→Rn应用到消息 s \mathcal{s} s以生成发送信号 x = f ( s ) ∈ R n \mathrm{x}=f(s)\in\mathbb{R}^n x=f(s)∈Rn。通常,发射端的硬件会对 x \mathrm{x} x加以限制,例如,能量限制 ∥ x ∥ 2 2 ≤ n \lVert\mathrm{x}\rVert^2_2\le n ∥x∥22≤n、幅度限制 ∣ x i ∣ ≤ 1 \lvert x_i\rvert\le1 ∣xi∣≤1 ∀ i \forall i ∀i或者是平均功率限制 E [ ∣ x i ∣ 2 ] ≤ 1 E[\vert x_i\vert^2]\le 1 E[∣xi∣2]≤1 ∀ i \forall i ∀i。该系统的通信速率为 R = k / n R=k/n R=k/n[bit/channel use],其中 k = log 2 ( M ) k=\log_2(M) k=log2(M)。在接下来的论文中,符号 ( n , k ) (n,k) (n,k)表示通讯系统发送 M = 2 k M=2^k M=2k信息(例如:k比特)通过 n n n个信道。我们将信道看做是一个条件概率函数 p ( y ∣ x ) \mathrm{p}(\mathrm{y|x}) p(y∣x),其中 y ∈ R n \mathrm{y}\in\mathbb{R}^n y∈Rn为接受信号,而后通过转换 g : R n → M g:\mathbb{R}^n\to\mathcal{M} g:Rn→M产生传输信号 s s s的估计 s ^ \hat s s^。
通常,自编码器的目标是在某个中间层找到其输入的低维表示,从而允许以最小误差重建输出。在我们的例子中,autoencoder的目的是不同的。换句话说,通常大多数自编码器是从输入数据中去除冗余的,但这种自编码器(“信道自编码器”)通常是增加冗余的,目的是学习一个对信道扰动具有鲁棒性的中间表示。
首先,我们需要寻找的自编码器能够学习一种 s \mathrm{s} s的表示 x \mathrm{x} x(用 x \mathrm{x} x来表示 s \mathrm{s} s);其次,这样的一种表示( x \mathrm{x} x)需要在信道损伤(例如:噪声、衰落、失真)的情况下,从 x \mathrm{x} x到 y \mathrm{y} y的映射是鲁棒的。这样,传输的消息可以以小的错误概率被恢复。
下图显示了这种自编码器的一个例子。

发射机由一个具有全连接的前馈NN组成,后面是一个规范化层,确保 x \mathrm{x} x上的物理约束得到满足。发射机的输入被编码为one-hot向量 1 s = R M 1_s=\mathbb{R}^M 1s=RM。信道由具有固定方差 β = ( 2 R E b / N 0 ) − 1 \beta=(2RE_b/N_0)^{-1} β=(2REb/N0)−1的噪声层表示,其中 E b / N 0 E_b/N_0 Eb/N0表示每比特能量( E b E_b Eb)与噪声功率密度( N 0 N_0 N0)之比。接收器也是由前馈NN实现。其最后一层使用softmax激活,其输出 p ∈ ( 0 , 1 ) M p\in(0,1)^M p∈(0,1)M是所有可能消息的概率向量。解码的消息 s ^ \hat{s} s^然后对应于具有最高概率的 p \mathrm{p} p的元素的索引。然后在所有所有可能的消息集 s ∈ M s\in\mathcal{M} s∈M上对输入 1 s 1_s 1s和输出 p \mathrm{p} p之间交叉熵损失函数进行随机梯度下降(SGD),其中交叉熵损失函数是最适合分类问题的。
2、性能及表示
(1)BLER比较

上左图(a)比较了使用BPSK调制、编码方式为汉明(7,4)编码、解码方式为硬解码或者最大似然解码情况下与自编码器(7,4)的块错误率(block error rete),例如 P r ( s ^ ≠ s ) Pr(\hat s\neq s) Pr(s^=s)比较,其中自编码器加以固定的能量限制 ∥ x ∥ 2 2 = n \lVert\mathrm{x}\rVert^2_2=n ∥x∥22=n。所有系统的通信速率均为 R = 4 / 7 R=4/7 R=4/7。作为比较,论文还选用了未编码的BPSK(4,4)作为对比。在没有任何先验知识的情况下,自编码器能够达到和汉明(7,4)编码、MLD解码的系统同样的性能。其中,自编码器的参数如下表所示。

其中,固定 E b / N 0 = 7 d B E_b/N_0=7\,dB Eb/N0=7dB,使用学习率为0.001的Adam优化器。
上右图(b)显示了相近的比较,只不过是针对(8,8)和(2,2)通讯系统。在(2,2)时,自编码器所取得的BLER和未编码的BPSK一致,但是在(8,8)通讯系统中,在信噪比接近于满信噪比时,自编码器表现的比未编码的BPSK更好。
####(2)学习到的表示 x \mathrm{x} x
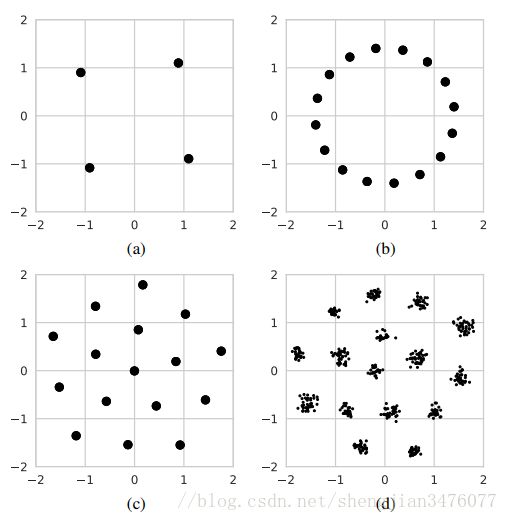
上图显示了系统学习到不同 ( n , k ) (n,k) (n,k)值的情况下,发送消息的表示 x \mathrm{x} x的复合星座点。对于上图(a),对于简单的(2,2)系统,表示 x \mathrm{x} x能够迅速收敛到有一定旋转的QPSk的星座点上;相近的,对于上图(b),(2,4)系统能够收敛到有旋转的16-PSK星座点上;上图©显示了在(2,4)系统中用平均功率标准化的限制替代固定能量标准化后的结果,能够达到和16-QAM调制一样的BLER;上图(d)使用了t-SNE对7维的表示 x \mathrm{x} x进行了降维,得到了和上述形状类似的簇排列。
四、autoencoder实现多发射端、多接收端通讯系统
1、信道模型
上述autoencoder实现的单发射端、单接收端通讯系统可以推广到多发射端、多接收端共享公共信道的通讯系统。

发射端1想发送消息 s 1 ∈ M \mathcal{s}_1\in\mathbb{M} s1∈M给接收端1,同时发射端2想发送消息 s 2 ∈ M \mathcal{s}_2\in\mathbb{M} s2∈M给接收端2。所有的发射端-接收端对均由NN实现,和上述实现的单发射端、单接收端通讯系统不同的是,发送的消息 x 1 , x 2 ∈ C n x_1,x_2\in\mathbb{C}^n x1,x2∈Cn在接收端是相互干扰的,导致在接收端得到的是有噪声的信号。 y 1 = x 1 + x 2 + n 1 \mathrm{y}_1=\mathrm{x}_1+\mathrm{x}_2+\mathrm{n}_1 y1=x1+x2+n1 y 2 = x 2 + x 1 + n 2 \mathrm{y}_2=\mathrm{x}_2+\mathrm{x}_1+\mathrm{n}_2 y2=x2+x1+n2其中, n 1 , n 2 ∼ C N ( 0 , β I n ) n_1,n_2\sim \mathcal{C}\mathcal{N}(0,\beta\mathrm{I}_n) n1,n2∼CN(0,βIn)为高斯噪声。为了简单,我们采用复值代替2n大小的实值向量,即 ( n , k ) (n,k) (n,k)表示每一个 2 k 2^k 2k消息通过 n n n个传输。用 l 1 = − log ( [ s ^ 1 ] s 1 ) , l 2 = − log ( [ s ^ 2 ] s 2 ) l_1=-\log([\hat{s}_1]_{s_1}),\quad l_2=-\log([\hat{s}_2]_{s_2}) l1=−log([s^1]s1),l2=−log([s^2]s2)表示各自通讯对的交叉熵损失函数,用 L ~ 1 ( θ t ) , L ~ 2 ( θ t ) \tilde{L}_1(\theta_t),\tilde{L}_2(\theta_t) L~1(θt),L~2(θt)表示和mini-batch t有关的损失函数。那么如何训练两对相互冲突的目标函数呢?一种方法即是最小化共同损失的加权和,例如 L ~ = α L ~ 1 + ( 1 − α ) L ~ 2 \tilde{L}=\alpha\tilde{L}_1+(1-\alpha)\tilde{L}_2 L~=αL~1+(1−α)L~2,其中 α ∈ [ 0 , 1 ] \alpha\in[0,1] α∈[0,1]。然而,对每个损失给定相同的权值(例如 α = 0.5 \alpha=0.5 α=0.5)并不必然导致相同的性能。在论文实验中,这种方法常导致不平等和局部结果。对于这种原因,我们采用第二种方法,即给定每一个mini-batch t一个动态权重 α t \alpha_t αt: α t = L ~ 1 ( θ t ) L ~ 1 ( θ t ) + L ~ 2 ( θ t ) , t > 0 \alpha_t=\frac{\tilde{L}_1(\theta_t)}{\tilde{L}_1(\theta_t)+\tilde{L}_2(\theta_t)},\quad t>0 αt=L~1(θt)+L~2(θt)L~1(θt),t>0其中,初始值 α 0 = 0.5 \alpha_0=0.5 α0=0.5。在实验中,该方法通常能够得到较优的结果。
2、性能及表示
(1)BLER比较

在实际实现通讯系统的过程中,需将复值转换成2n大小的实值向量进行训练。作为对比,实验以未编码的 2 2 k / n − Q A M 2^{2k/n}-QAM 22k/n−QAM为基准,其中通过时分复用共享传输信道。如上图所示,在(1,1)和(2,2)情况下,自编码器和TS(time-sharing)有相同的性能;在(4,4)和(4,8)情况下,随着信噪比增大,自编码器展现出更明显的优势。
(2)学习到的表示 x \mathrm{x} x

如上图(a)所示,对于(1,1),学习到了类似于BPSK经过一定旋转的星座图;然而,如上图(b)所示,对于(2,2),学习到的表示并不是正交的,但可以看做是叠加编码;对于(4,4)和(4,8),星座图更加难以解释,但是我们可以看到两个发射端的星座图类似椭圆,正交主轴和焦距不同,这在(4,8)表现的更加明显。
##五、用于增强信号处理算法的RTN(无线转换网络)
在通信信道以及收发机硬件中,信号常会发生改变,但这些往往可以通过紧凑的参数模型/变化来转换,常用的变换和估计包括符号/时钟定时重采样,与估计载频混合,并与反向信道脉冲进行卷积。参数估计复杂且和信号特定的属性有关,故本文提出一种改进的加入专家知识,且不只针对特定的信号假设的DL模型,其结构如下图所示。其主要包括三个部分: ( i ) (\mathrm{i}) (i)学习到的参数估计器 g ω : R n → R p g_\omega:\mathbb{R}^n\to\mathbb{R}^p gω:Rn→Rp,从输入 y \mathrm{y} y计算一个参数向量 ω ∈ R p \omega\in\mathbb{R}^p ω∈Rp;(ii)参数转换t: R n × R p → R n ′ \mathbb{R}^n\times\mathbb{R}^p\to\mathbb{R}^{n'} Rn×Rp→Rn′,即将确定性的函数应用于由 ω \omega ω进行参数化并适合于传播现象的 y \mathrm{y} y;(iii)判别网络 g \mathbb{g} g: R n ′ → M \mathbb{R}^{n'}\to\mathcal{M} Rn′→M,即从标准化的 y ˉ ∈ R n ′ \bar{\mathrm{y}}\in\mathbb{R}^{n'} yˉ∈Rn′中产生出传输信号的估计 s ^ \hat s s^。

需要注意的是,上述的RTN训练目标并不是为了得到参数估计器本身,而是为了通过参数估计的方式获得更好的端到端的性能。
针对上述的RTN,一个简单而有效的例子即是相偏估计和补偿,假定 y c = e j φ y ~ c ∈ C n \mathrm{y}_c=\mathrm{e}^{\mathcal{j}\varphi}\tilde{\mathrm{y}}_c\in\mathbb{C}^n yc=ejφy~c∈Cn为经历了相偏 φ \varphi φ的IQ采样向量,并令 y = [ R { y } T , S { y } T ] T ∈ R 2 n \mathrm{y}=[\mathfrak{R}\{\mathrm{y}\}^T,\mathfrak{S}\{\mathrm{y}\}^T]^T\in\mathbb{R}^{2n} y=[R{y}T,S{y}T]T∈R2n,估计器 g \mathbb{g} g的目标是学习一个相偏 φ \varphi φ的估计 φ ^ = ω = g ω ( y ) \hat\varphi=\omega=\mathbb{g}_\omega(\mathrm{y}) φ^=ω=gω(y),然后用于参数转换 t \mathbb{t} t来计算 y ˉ c = e − j φ y c \bar{\mathrm{y}}_c=\mathrm{e}^{-\mathcal{j}\varphi}\mathrm{y}_c yˉc=e−jφyc。于是得到规范化的信号 y ˉ = [ R { y ˉ c } T , S { y ˉ c } T ] T ∈ R 2 n \bar{\mathrm{y}}=[\mathfrak{R}\{\bar{\mathrm{y}}_c\}^T,\mathfrak{S}\{\bar{\mathrm{y}}_c\}^T]^T\in\mathbb{R}^{2n} yˉ=[R{yˉc}T,S{yˉc}T]T∈R2n,具体的由下式给出: y ˉ = t ( φ ^ , y ) = [ cos ( φ ^ ) R { y ˉ c } + sin ( φ ^ ) S { y ˉ c } cos ( φ ^ ) S { y ˉ c } − sin ( φ ^ ) R { y ˉ c } ] \bar{\mathrm{y}}=\mathbb{t}(\hat{\varphi},\mathrm{y})=\left[\begin{matrix}\cos(\hat{\varphi})\mathfrak{R}\{\bar{\mathrm{y}}_c\}+\sin(\hat\varphi)\mathfrak{S}\{\bar{\mathrm{y}}_c\}\\\cos(\hat\varphi)\mathfrak{S}\{\bar{\mathrm{y}}_c\}-\sin(\hat\varphi)\mathfrak{R}\{\bar{\mathrm{y}}_c\}\end{matrix}\right] yˉ=t(φ^,y)=[cos(φ^)R{yˉc}+sin(φ^)S{yˉc}cos(φ^)S{yˉc}−sin(φ^)R{yˉc}]然后将得到的 y ˉ \bar{\mathrm{y}} yˉ送入到判别网络 g \mathbb{g} g进一步的处理。
文章比较了调制方式为DBPSK(8,7)、编码方式为汉明(7,4)码并使用MLSE均衡得到的结果与未使用RTN、使用了RTN的自编码器(8,4)进行相应的比较,比较结果如下图所示。
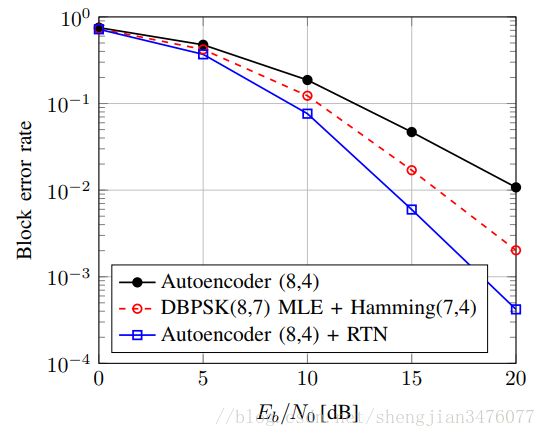
其中信道类型为多径衰落信道,信道抽头系数 L = 3 \mathrm{L}=3 L=3,则接受信号 y = [ R { y } T , S { y } T ] T \mathrm{y}=[\mathfrak{R}\{\mathrm{y}\}^T,\mathfrak{S}\{\mathrm{y}\}^T]^T y=[R{y}T,S{y}T]T可以由下列公式给出: y c , i = ∑ l = 1 L h c , l x c , i − l + 1 + n c , i \mathbb{y}_{c,i}=\sum^{L}_{\mathscr{l=1}}\mathbb{h}_{c,l}x_{c,i-l+1}+n_{c,i} yc,i=l=1∑Lhc,lxc,i−l+1+nc,i其中, h c ∼ C N ( 0 , L − 1 I L ) h_c\sim\mathcal{CN}(0,L^{-1}\mathrm{I}_L) hc∼CN(0,L−1IL)是独立同分布的瑞利信道抽头, n c ∼ C N ( 0 , ( R E b / N 0 ) − 1 I n ) n_c\sim\mathcal{CN}(0,(RE_b/N_0)^{-1}\mathrm{I}_n) nc∼CN(0,(REb/N0)−1In)是接收端噪声。 x c ∈ C n \bf\mathrm{x}_c\in\mathbb{C}^n xc∈Cn是输入信号,其中我们假定 x c , i = 0 i ≤ 0 x_{c,i}=0\;i\le0 xc,i=0i≤0。这里的参数估计器是预测一个复值的参数向量 ω c \omega_c ωc(使用2倍长度的实值代替),送入到参数转换与 y c \mathrm{y}_c yc做复卷积,即RTN通过逆滤波补偿信道输出。其中估计器由两层全连接的神经网络构成,内层的激活函数为tanh函数,输出层激活函数为线性激活函数。
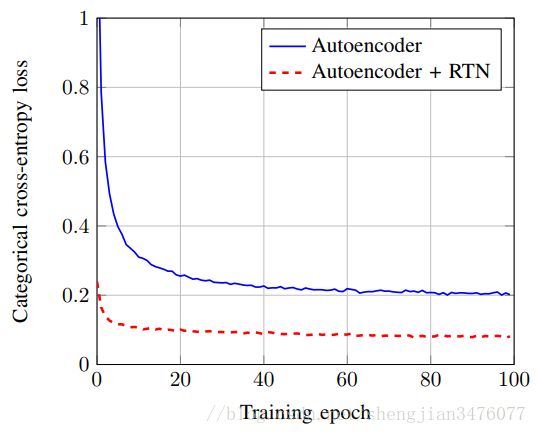
在上述比较中,具有RTN的自编码器相对于没有RTN的自编码器和调制方式为DBPSK(8,7)、编码方式为汉明(7,4)码并使用MLSE均衡得到的结果都有更优的结果。具有RTN的自编码器在训练中收敛的速度更快,结果如下图所示。
六、使用CNN做分类任务
在之前的很长一段时间里,一直有人尝试用机器学习的方法对调制类型进行分类,如决策树、支持向量机、随机森林或小型前馈神经网络。还有一个方法是使用在利用专家知识提取得到的特征映射上进行模式识别,,例如谱相关函数结合神经网络进行分类。但是却没有在原始数据上进行分类的方法,故本文提出一种卷积神经网络应用在原始数据上进行分类,其结构如下图所示。

其中训练数据采用的是RML2016.10b数据集,该数据集包括1.2M的IQ采样数据,其中包括10中不同的数字调制方式。其数据集为真实的无线信道采样数据,包括多径衰落、采样率和中心频偏等差别,其信噪比为 − 20 d B -20\,dB −20dB到 18 d B 18\,dB 18dB之间的20个不同值。文章对比了随机猜测、决策树、提升树以及CNN的分类结果,如下图所示。
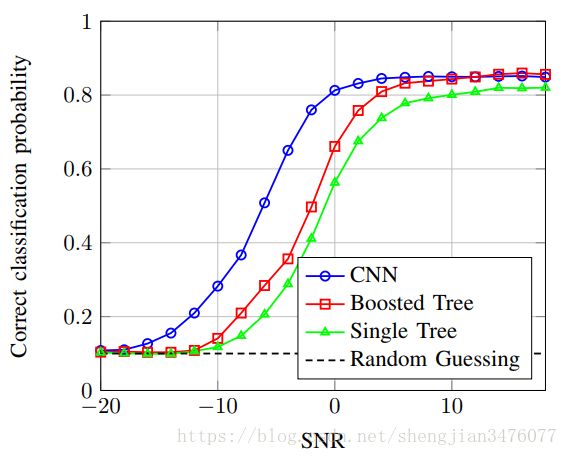
很明显,在低信噪比的情况下,CNN分类取得了更好的分类结果。单就CNN而言,结果如下图的混淆矩阵图所示。
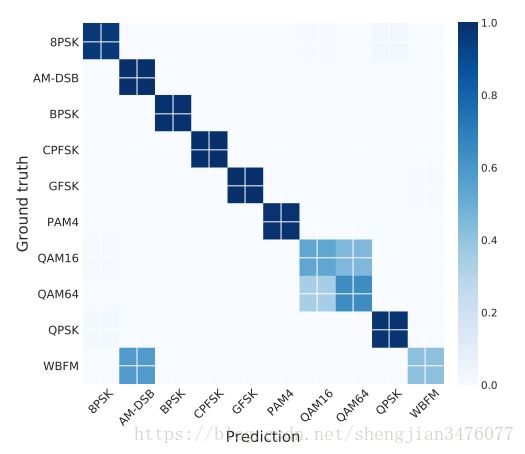
其中,上图的实验结果是在 S N R = 10 d B \mathrm{SNR}=10\,dB SNR=10dB的情况下得到的。我们可以看到,在高信噪比情况下,CNN仍然难以区分出AM-DSB和WBFM。其混淆主要发生在潜在的语音信号空闲或者没有承载很多信息的时候。而在短时观察少量信号的情况下很难区分QAM16和QAM64。
七、存在的问题和挑战
1、数据集的挑战
在计算机视觉、语音识别以及自然语言处理领域有统一的数据集进行比较,而在通讯领域暂时还没有统一的数据集进行比较,那么在实际的实验中,对实验结果就会存在较大的分歧。
2、数据表示、损失函数和训练环境的信噪比
深度学习应用于通讯是一个新的领域,所以对于数据的表示、损失函数选取以及训练策略所知甚少。
3、复值神经网络
现有的神经网络还不能够支持对于复数值的训练和优化。
4、深度学习增强算法
当传输的数据集 M \mathcal{M} M是一个大型的数据集时,如 k = 100 b i t s k=100\,bits k=100bits,则 M = 2 100 M=2^{100} M=2100可能的消息,这对于神经网络而言将是难以处理的维数灾难。
5、端到端学习的系统认知
在上述的端到端的学习过程中,论文默认知道信道的类型及参数,这样才能使得神经网络的反向传播算法能够得到有效计算。在信道类型或信道模型参数未知的情况下,神经网络难以进行有效的传播和训练,将无法正常工作。
6、从CSI中学习
精确的信道状态信息(CSI)是多用户MIMO系统的基础,但是当前对于该信息使用甚少,对于ML模型,可以尝试从CSI中学习和建模。