入侵检测IDS学习--snort基础

1.在linux下面使用libpcap收发包，如果写的代码只做发包，那么速度是很快，如果代码做多线程，一个收包，一个发包，一旦发包比较多，就会开始丢失，而且速度相当的慢。

1.BM算法

BM匹配算法是Boyer和Moore两人在KMP算法的启发下，提出的一种字符串快速匹配算法。它采用自右向左的方式扫描模式(P表示)与正文（T表示），一旦发现正文中出现模式中没有的字符时就可以将模式、正文进行一个大幅度的偏移。模式与正文在匹配比较的过程中，将P与T 左对齐，即P[1]与T[1]对齐。匹配从P 的 最右端字符开始，判断P[strlen(P)](strlen(p)为模式长度)与T[strlen(P)]是否匹配，如果匹配成功，则继续判断P[strlen(P)-1]与T[strlen (P)-1]是否匹配，如此反复比较，直到P中的所有字符全部匹配成功或是有不匹配的字符出现。其移动遵循以下规律：
a．坏字符移动，当发生不匹配时，移动模式串使得不匹配的正文字符与该字符在模式串中的最右出现对齐。如果字符没有在模式中出现，移动距离为字符到模式首位的长度；如果字符在模式中出现，移动模式中字符出现位置到正文字符处；

b．好后缀移动，当匹配过程中发生不匹配时，如果已匹配子串长度不为0，且匹配子串在模式串中有相同的其他子串，移动模式串使得已匹配部分与该部分在模式串中的最右端出现对齐。

BM算法先对模式P进行预处理，计算两个偏移函数:Bad_Char(针对某个字符)和Good_Suffix(针对某个子串)，然后将文本和模式对齐，从右往左进行匹配，当文本字符与模式字符失配时，根据函数BadChar和Good_Suffix计算出的偏移值，取两者中的大者，将文本指针往右移，匹配成功则予以输出。

例如：设正文为“otootowtmwotwom”要在其中搜索“ttowtow”；
正文Text  ：otootowtmwotwom
模式Pattern：ttowtow  初始状态
模式Pattern： ttowtow  根据坏字符移动一个字符
模式Pattern：      ttowtow  根据好后缀移动3个字符

2.AC算法
AC算法是基于FSA（有限状态自动机）的，在进行匹配之前先对模式串集合P进行预处理，形成树型FSA－AC状态机(AC state machine)，然后只需对文本串T扫描一次就可以找出与其匹配的所有模式串。有限自动机的基本思想是根据输入和当前的状态决定下一个状态和输出，接着再进入下一次输入。有限自动机的构造过程是将模式串集合变换成由转向函数，失效函数和输出函数组成的树型有限自动机。模式匹配的处理过程就变成了状态转换的处理过程。

有限自动机的构造中，每个模式串的字符是从前到后依次加到树型的有限自动机中的，在匹配时，目标串的输入，即匹配过程，也是按照从前到后的次序。预处理生成3个函数：goto（转移）函数，failure（失效）函数和output（输出）函数。
设U={0，1，2…}为状态集合，转移函数g：(U,Sp)→U为一映射，其建立过程为：逐个取出Sp中模式串的每个字符，从状态0出发，由当前状态和新取出的字符决定下一状态。如果有从当前状态出发并标注该字符的矢线，则将矢线所指的状态赋为当前状态，否则，添加一个标号比已有状态标号大1的新状态，并用一条矢线从当前状态指向新加入的状态，并将新加入的状态赋为当前状态。Sp中的所有模式串处理完后，再画一条从0状态到0状态的自返线，标注的字符为不能从0开始的字符集。例如，Sp={he,she,his,hers}的goto函数如图5-2所示：

失效函数f用来指明当某个模式与文本匹配不成功时，应处理的下一状态。f的构造方法为：所有第一层状态的失效函数为0，如f(1)=f(3)=0；对于非第一层状态s，若其父状态为r（即存在字符a,使g(r,a)=s），则f(s)=g(f(s*),a)，其中状态s*为追溯s 的祖先状态得到的第一个使g(f(s*),a)存在的状态。如f(4)=g(f(3),h)=g(0,h)=1，f(5)=g(f(4),e)=g(1,e)=2。失效函数把一个状态匹配到另一个状态。f的值如表3-1所示：

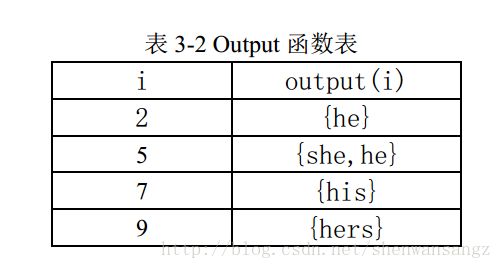
输出函数output的作用是在匹配过程中输出已经匹配的模式串。output的构造分两步，第一步是在构造转移函数g时，每处理完一个模式串，则将该模式串加入到当前状态s的输出函数中，如output(2)={he},output(5)={she}。第二步是构造失效函数f时，若f(s)=s’,则output(s)=output(s)∪output(s’), 如output(5)=output(5)∪output(2)={she,he}。goto函数图中黑粗圈的状态表示有输出，output的值如下：其他状态的输出为空。

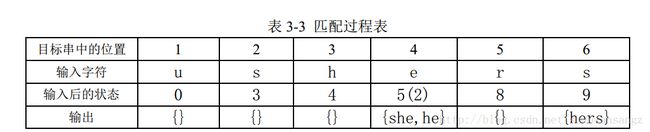
对于上面的模式串集合Sp={he,she,his,hers}，假设文本T为ushers。当状态机M在状态4的时候并且当前的输入是e，因为g(4,e)＝5，自动机进入状态5，表明已经在输入文本字符串的第四个字符末尾处发现关键字“she”和“he”。在状态5，当输入字符是r时，自动机完成两个状态转换。因为g(5,r)＝fail，所以M的输入状态为2＝f(5)。由于g(2,r)＝8。M把8作为输入状态继续下一个输入字符。在这个状态转换循环，没有输出状态，具体匹配过程如下：