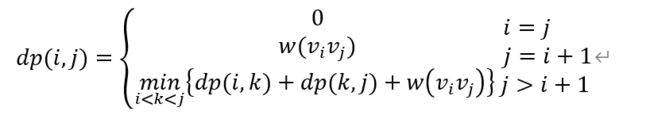dp：最优三角剖分

一凸 8 边形 P 的顶点顺时针为{v 1 ， v 2 ， … ， v 8 }，任意两顶点间的线段的权重由矩阵 D 给出。若 v i 与 v j 是 P 上不相邻的两个顶点，则线段 v i v j 称为 P 的一条弦。求 P 的一个弦的集合 T，使得 T 中所有的弦恰好将 P 分割成互不重迭的三角形，且各三角形的权重之和为最小（一个三角形的权重是其各边的权重之和）。

本题，我们设dp(i, j)表示从顶点i到顶点j对应的最优权值为dp(i, j)，那么可以分为以下三种情况

（1）i == j

此时顶点i和顶点j重合，根本就没有边，所以权值为0

（2）j = i + 1
这种情况顶点i和顶点j相邻，因此也最优权值应当为顶点i和顶点j之间的权重，即w(i, j)

（3）j > i + 1

这种情况说明顶点i和顶点j之间还有其他顶点k，k的范围应该是i < k < j，那么应该将问题拆成两个递归子问题，一部分是顶点i到顶点k的最优权重，另一部分是顶点k到顶点j的最优权重，别忘了还要加上顶点i到顶点j之间本身的权重，即w(i, j)

因此递归表达式可以如下定义

因此我们最终求得的值应该是dp(1, 8)，即从顶点1到顶点8的最优权重，但是由于该算法中每个弦只算了一次，我们要求所有三角形的权值之和，因此每个弦应当计算两次，所以我们还要在原有dp(1, 8)的基础上再加上所有弦的权值之和，即为最终我们要求的答案。

#include 
#include 
#include 


void traceback(int i, int j, int d[][8], int dp[][8], int s[][8], int *sum_address) {
    int distance_left, distance_right;
    int k;
    k = s[i][j];
    distance_left = abs(i - k);
    distance_right = abs(j - k);
    if (distance_left == 1 && distance_right != 1) {
            printf("emm %d\n", d[k][j]);
        (*sum_address) += d[k][j];
        printf("%d %d %d\n", i, j, k);
        traceback(k, j, d, dp, s, sum_address);
    }
    else if (distance_left != 1 && distance_right == 1) {
        printf("emm %d\n", d[i][k]);
        (*sum_address) += d[i][k];
        printf("%d %d %d\n", i, j, k);
        traceback(i, k, d, dp, s, sum_address);
    }
    else if (distance_left != 1 && distance_right != 1) {
        traceback(i, k, d, dp, s, sum_address);
        traceback(k, j, d, dp, s, sum_address);
    }
    else {
        return;
    }
}

int main()
{
    int i, j, step, k;
    int temp_min, temp_k;
    int d[8][8] = {{0, 14, 25, 27, 10, 11, 24, 16},
                  {-1, 0, 18, 15, 27, 28, 16, 14},
                  {-1, -1, 0, 19, 14, 19, 16, 10},
                  {-1, -1, -1, 0, 22, 23, 15, 14},
                  {-1, -1, -1, -1, 0, 14, 13, 20},
                  {-1, -1, -1, -1, -1, 0, 15, 18},
                  {-1, -1, -1, -1, -1, -1, 0, 27},
                  {-1, -1, -1, -1, -1, -1, -1, 0}};
    int dp[8][8];
    int s[8][8];
    int sum = 0;
    for (i = 0; i < 8; i++) {
        for (j = 0; j < 8; j++) {
            dp[i][j] = s[i][j] = 0;
        }
    }
    for (i = 0; i < 8; i++) {
        dp[i][i + 1] = d[i][i + 1];
    }
    for (step = 2; step <= 7; step++) {
        for (i = 0; i <= 7 - step; i++) {
            j = i + step;
            temp_min = 65535;
            for (k = i + 1; k < j; k++) {
                if (d[i][j] + dp[i][k] + dp[k][j] < temp_min) {
                    temp_min = d[i][j] + dp[i][k] + dp[k][j];
                    temp_k = k;
                }
            }
            dp[i][j] = temp_min;
            s[i][j] = temp_k;
        }
    }
    for (i = 0; i < 8; i++) {
        for (j = 0; j < 8; j++) {
            printf("%3d ", dp[i][j]);
        }
        printf("\n");
    }
    printf("\n");
    for (i = 0; i < 8; i++) {
        for (j = 0; j < 8; j++) {
            printf("%3d ", s[i][j]);
        }
        printf("\n");
    }
    printf("\n");
    traceback(0, 7, d, dp, s, &sum);
    printf("\n");
    printf("final result: %d + %d = %d\n", sum, dp[0][7], sum + dp[0][7]);
    return 0;
}