多尺度小波分解Matlab/Python实现与原理分析

小波分解的理解

Matlab中实现小波分解方式

在matlab中实现小波分解的方式比较简单，通过[C,L] = wavedec(X,N,‘wname’)得到C和L，如下图，C表示分解得到的各个层的小波系数，L表示各个层的长度，L的最后一个数表示原数据的长度。

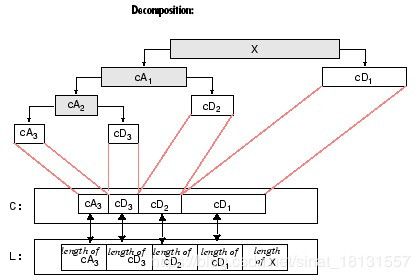
通过在Matlab中输入open wavedec打开分解的源文件可以发现，主要就是通过执行dwt函数进行多层分解的，分解的系数通过wfilters函数获得Lo_D,Hi_D，在分解中[x,d] = dwt(x,Lo_D,Hi_D);不断使用分解得到的x作为下一次分解的输入。进一步地，打开dwt文件，还能看到为了抑制边界效应的边界延拓通过wextend完成，卷积是通过wconv1实现的。分解工作的流程图为：

结果返回

输入数据

wavedec函数

dwt函数

wextend端点延拓方法

wconv1卷积

间隔取值

分解得到的每个层的长度可以表示为：
$$L_i=\frac{{\mathrm{L}}_{\mathrm{i}-1}+滤波器长度-1}{2}$$
滤波器长度可以查看Matlab，如sym7的长度为14，sym4的长度为8。
分解之后，可以通过X = waverec(C,L,‘wname’)重构出来，当需要去除某个层的信息，达到移除噪声（低层分解的细节部分）或者移除基线漂移（高层分解的平均部分），可以通过X = wrcoef(‘type’,C,L,‘wname’,N)得到某个level的‘a’或者’d’(type = ‘a’或者‘d’),用原始信号减去该部分即可。

小波分解实现原理

但是在其他的编程环境中，往往只有基础的DWT和IDWT用于做单层的小波变换，多尺度分解的wrcoef函数是没有实现的，得到的C的长度不一，不能直接重构。
实现的原理即为：不断对信号进行小波分解，
信号s经过一次小波分解后得到平均cA1和细节cD1，然后将cA1作为输入进行下一次小波分解得到平均cA2和细节cD2,然后将cA2作为输入进行下一次小波分解得到平均cA3和细节cD3…。假如进行3个尺度的分解，得到的C即为：
$C=[cA3,cD3,cD2,cD1]$
令不要的层的系数变为0，向上重构，例如如果需要去除基线漂移的话，就是细节部分cA3令为0，然后用令为0的cA3和cD3重构一次得到重构的cA2，cA2和cD2重构得到cA1，cA1和cD1重构得到信号s。
通过这种方式写的Matlab验证脚本为：

x = [0:500];
subplot(211)
plot(x,'-');hold on;
subplot(212)
[C,L] = wavedec(x,6,'sym7');
a = wrcoef('a',C,L,'sym7',6);
r1 = x - a;
plot(r1,'b');

%% 第二种方式
C(1:L(1)) = zeros(1,L(1));
r2 = waverec(C,L,'sym7');
plot(r2,'k');
%% 第三种方式
[C1,L1] = wavedec(x,1,'sym7');
[C2,L2] = wavedec(C1(1:L1(1)),1,'sym7');
[C3,L3] = wavedec(C2(1:L2(1)),1,'sym7');
[C4,L4] = wavedec(C3(1:L3(1)),1,'sym7');
[C5,L5] = wavedec(C4(1:L4(1)),1,'sym7');
[C6,L6] = wavedec(C5(1:L5(1)),1,'sym7');

C6(1:L6(1)) = zeros(1,L6(1));
x5 = waverec(C6,L6,'sym7');
C5(1:L5(1)) = x5;
x4 = waverec(C5,L5,'sym7');
C4(1:L4(1)) = x4;
x3 = waverec(C4,L4,'sym7');
C3(1:L3(1)) = x3;
x2 = waverec(C3,L3,'sym7');
C2(1:L2(1)) = x2;
x1 = waverec(C2,L2,'sym7');
C1(1:L1(1)) = x1;
r3 = waverec(C1,L1,'sym7');
plot(r3,'r');

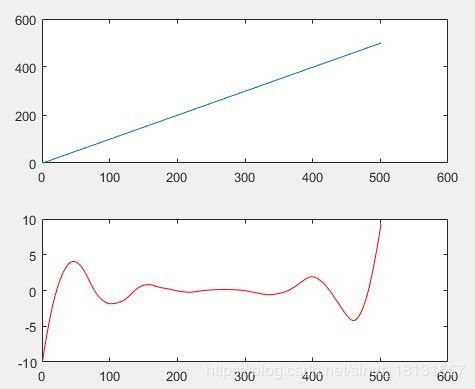
可以看到三种重构的方式结果是一样的，subplot（212）的三种方式去除了cA6之后是完全一样的，当其他编程环境中需要使用到类似的处理效果可以参考这个逻辑。

Python环境下的实现为：

    def waveletdec(self, s, coef_type='d', wname='sym7', level=6, mode='symmetric'):
        import pywt
        N = len(s)
        w = pywt.Wavelet(wname)
        a = s
        ca = []
        cd = []
        for i in range(level):
            (a, d) = pywt.dwt(a, w, mode)  # 将a作为输入进行dwt分解
            ca.append(a)
            cd.append(d)
        rec_a = []
        rec_d = []
        for i, coeff in enumerate(ca):
            coeff_list = [coeff, None] + [None] * i
            rec_a.append(pywt.waverec(coeff_list, w)[0:N])  # 进行重构
        for i, coeff in enumerate(cd):
            coeff_list = [None, coeff] + [None] * i
            rec_d.append(pywt.waverec(coeff_list, w)[0:N])  # 进行重构
        if coef_type == 'd':
            return rec_d
        return rec_a