机器学习之十大算法入门

一、决策树（有监督算法）原理就是条件熵

特点：
1、只能接受离散特征 分类决策树
2、准确类不高，可解释性强，可视化
3、贪心算法，无法从全局的观点来观察决策树，从而难以调优
4、决策树算法可以看成把多个逻辑回归算法集成起来

熵：把熵用在集合上，熵越低越好，越低越好做决策。熵越高不确定性越高
熵的取值范围是（0 ,无穷大）
计算公式：

H(X)=E[I(xi)]=−∑i=1nPilogpi H ( X ) = E [ I ( x i ) ] = − ∑ i = 1 n P i l o g p i

条件熵的计算：H(Label|某个特征) Label是标注，这个条件熵反映了在知道该特征时，标签的混乱程度，这个条件熵可以帮助我们选择特征，选择下一步的决策树的节点
gini指数 在scikit当中，decisiontreeclassifuer默认是用gini
gini指数的取值范围(0,1)

决策树：
a.叶子节点上的最小样本数太少，缺乏统计意义
b.二分类，正负样本数目相差是否悬殊，投票机制
c.从叶子结点的情况，可以看出决策树的质量，发现有问题束手无策
d.决策树层次太深，容易过拟合，要剪枝
决策树的可视化：

剪枝：在某个节点上不再继续分叉，而是直接替换为叶子节点。这个叶子节点所标识的类别，按照少数服从多数的原则来确定。
剪枝的方法:
预剪枝:限制树的深度，叶子节点的个数，叶子节点的样本数，信息增益等。
后剪枝（Post-Pruning）:决策树构造完成后进行剪枝。后剪枝是目前最普遍的做法

二、K-means算法 （无监督算法，聚类算法）

最常用的无监督算法，选将军模型 。也是随机算法，用到了随机试验。

1、主要特点：

常用距离
a.欧式距离
b.曼哈顿距离
应用:
a.去除孤立点，离群点，只针对度量算法，解决方法（常用归一化预处理方法 ）
b.离散化

2、算法流程：

1.选择聚类的个数k（kmeans算法传递超参数的时候，只需设置最大的K值）
2.任意产生k个聚类，然后确定聚类中心，或者直接生成k个中心。
3.对每个点确定其聚类中心点。
4.再计算其聚类新中心。
5.重复以上步骤直到满足收敛要求。（通常就是确定的中心点不再改变。）

3、kmeans作用：去除奇异值

应为EM算法，kmeans肯定会稳定到K个中心点
kmeans算法k个随机初始值怎么选？
要多选几次，比较，找出最好的那个。
a.bi-kmeans方法，依次补刀
b.层次聚类 k = 5，找到5个中心点，接着把这个5个中心点喂给kmeans，初始中心点不同，收敛的结果也可能不一样的

K值确定：
Elbow method就是“肘”方法，对于n个点的数据集，迭代计算k from 1 to n，每次聚类完成后计算每个点到其所属的簇中心的距离的平方和，可以想象到这个平方和是会逐渐变小的，直到k==n时平方和为0，因为每个点都是它所在的簇中心本身。但是在这个平方和变化过程中，会出现一个拐点也即“肘”点，下图可以看到下降率突然变缓时即认为是最佳的k值。
肘方法的核心指标是SSE(sum of the squared errors，误差平方和)， Ci是第i个簇，
p是Ci中的样本点， mi是Ci的质心（Ci中所有样本的均值）， SSE是所有样本的聚
类误差，代表了聚类效果的好坏。

SSE=∑i=1k∑p∈Ci|p−mi|2 S S E = ∑ i = 1 k ∑ p ∈ C i | p − m i | 2

肘方法的核心思想：
随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。这也是该方法被称为肘方法的原因。

轮廓系数：
（ Silhouette Coefficient）结合了聚类的凝聚度（ Cohesion）和分离度
（ Separation），用于评估聚类的效果。该值处于-1~1之间，值越大，表示聚类效果
越好。

S=(b−a)max(a,b)S∈[−1,1] S = ( b − a ) m a x ( a , b ) S ∈ [ − 1 , 1 ]

a是Xi与同簇的其他样本的平均距离，称为凝聚度；
b是Xi与最近簇中所有样本的平均距离，称为分离度。

最近簇的定义：

Cj=argminCk1n∑p∈Ck|p−Xi|2 C j = a r g m i n C k 1 n ∑ p ∈ C k | p − X i | 2

其中p是某个簇Ck中的样本。即，用Xi到某个簇所有样本平均距离作为衡量该点到该簇的距离后，选择离Xi最近的一个簇作为最近簇。
求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。平均轮廓系数的取值范围为[-1,1]，且簇内样本的距离越近，簇间样本距离越远，平均轮廓系数越大，聚类效果越好。

聚类效果怎么判断？
1、SSE误差平方和越小越好，肘部拐点的地方。
2、也可用轮廓系数表示 系数越大，聚类效果越好，簇与簇之间距离越远

kmeans算法的最大弱点：只能处理球形的簇（理论）

三、KNN算法 有监督算法，效率低下（要找最近的邻居）

有监督算法，邻居是已知的，被标注的，没有迭代
特点：
1、其中K表示k个邻居，不表示距离
2、用在推荐系统，结合pearson距离，填充缺失值
3、处理非线性问题
4、KNN更适合处理一些分类规则相对复杂的问题
调优方法：K值得选择，k值越小，容易过拟合

四、SVM算法 支持向量机

特点：
1、SVM是介于简单算法和神经网络之间最好的算法
2、处理非线性问题
3、由于支持向量点离超平面有一定距离，有缓冲区，不容易过拟合
4、弱点：计算量大
核函数：高斯核函数（RBF）

五、逻辑回归 线性算法

特点：
1、线性回归，GLM广义线性模型的一种特殊情况
2、可以看成是最简单的神经网络
3、对数似然函数（损失函数），求最大值，损失函数越大越好
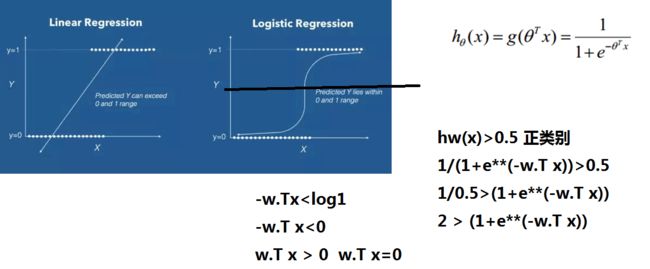
4、逻辑回归的决策边界是一条直线（不是曲线） 如图：决策树的可视化图中逻辑回归中的黑线

逻辑回归和线性回归：
1、逻辑回归用于分类，有2个类别的数据。 例如：医疗
2、线性回归用于模拟，只有一个类别的数据，尽可能让数据点在直线附近 例如：房价预测

w1 和w2是权重，sigma是求和，公式如下： f(x)=sigmaid(wTx+b) f ( x ) = s i g m a i d ( w T x + b )

六、朴素贝叶斯

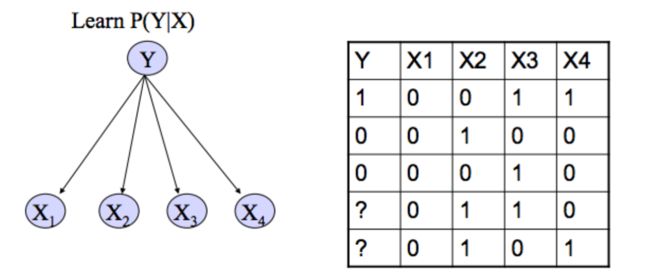
P(Y|X)节点一般表示离散的事件，射线表示条件概率，不能有闭环

特点：
1. 满足独立性假设的情况下，效果较好。 (特征多的时候，因为互相抵消的作用。效果反
而比较好，而且不要求独立性假设。 2.如果特征很多，往往独立性的条件不重要，可以用朴素贝叶斯
3. 算法简单容易实现，参数少(P(y), 条件概率表)，不能处理复杂的问题。
但是也是因为参数少，所以需要的：训练样本不多(与其他算法相比)。
参数少 求解空间维数低 不容易出现数据稀疏(sparse)
4. 可以处理多分类问题。很多分类算啊都只能处理2元分类问题
5. 可以处理非线性问题
6. 朴素贝叶斯只能处理离散问题(不是绝对的)

缺点：准确率不高

七、马尔可夫模型

特点：
1、马尔可夫得到模型容易，但是用模型需要推理，工作量很大
2、马尔可夫没有箭头，可以有环路
3、马尔可夫比较常用
4、马尔可夫模型（Markov Model）是一种统计模型，广泛应用在语音识别，词性自动标注，音字转换，概率文法等各个自然语言处理等应用领域。

affinity亲和力
energy(a,b,c)规律性的东西，并不一定是概率，但是可以表示ABC之间的一种亲和力
potential = e1 * e2 * e3…*en 一般来说不是概率
protential 归一化 -> 概率分布 probability
人体姿势识别，构造energy的时候，角度，长度参数
==结论：==
Bayes nodel 和 markov model ：任何一bayes model对应于唯一个markov model，而任意一个markov model，可以对应多个bayes model

EM算法是概率图算法的一个简单的

八、随机森林

本质上是将多个算法平等的聚集在一起
特点：
1、最简单的集成算法
2、随机性的引入使得随机森林不容易陷入过拟合，具有很好的抗噪能力。有效的缓解了单颗决策树容易过拟合的问题

算法思想：
RandomForest，每个单个的决策树，都是基于：
1.随机生的训练集
2.随机生成的特征集，来进行训练而得到的