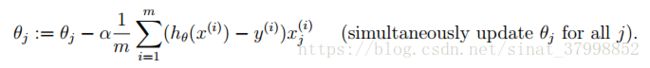斯坦福大学machine learning课程学习笔记
第1、2周课程及编程作业1
(基于matlab/octave语言)
一、第1、2周相关笔记
1、线性回归的梯度下降
feature scaling(特征缩放):
把每个特征缩放到一个合适的范围内,如[-1,1],[0,3](可以转为[-3,3]),[-2,0.5](可以转为[-2,2])等。
目的:为了使梯度下降的效率更高,下降的次数减少,速度加快。示意图如下:
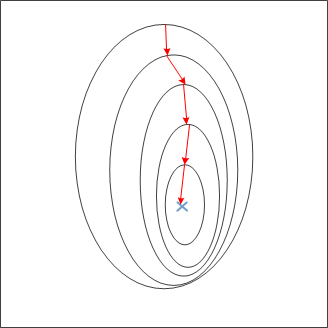
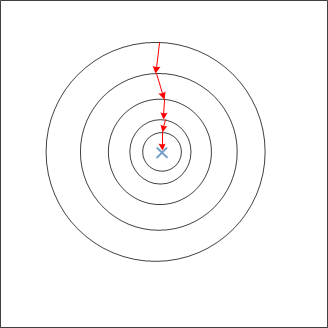
- 均值归一化(mean normalization)
将特征进行标准化,常用的方法有均值标准化(mean normalization):
即: xi x i 用 xi−ui x i − u i 来代替,使得特征有近似为0的均值。
其中 ui u i 表示特征的均值, σi σ i 表示特征的 标准差或 max-min ,
2、梯度下降的学习率 α α 如何选择
二、线性回归的实现(ex1.m)
1、warmUpExercise.m
该函数的功能是生成一个5*5的单位矩阵(正对角线为1,其它位置为0的矩阵)。有两种方法实现:
(1)使用matlab中的函数eye():A=eye(5)。
eye()函数用来生成单位矩阵。
A = eye(m):生成m*m单位矩阵;
A = eye(m,n):生成m*n单位矩阵;
A = eye([m,n]):生成m*n单位矩阵;
A = eye(size(A)):生成与A一样大小的单位矩阵。
(2)直接使用程序语句生成矩阵,具体就不写了,通过循环语句控制,对角线位置上置为1,其它位置置为0。
warmUpExercise.m完整代码:
function A = warmUpExercise()
%WARMUPEXERCISE Example function in octave
% A = WARMUPEXERCISE() is an example function that returns the 5x5 identity matrix
A = [];
% ============= YOUR CODE HERE ==============
% Instructions: Return the 5x5 identity matrix
% In octave, we return values by defining which variables
% represent the return values (at the top of the file)
% and then set them accordingly.
A=eye(5); %直接使用eyes函数来生成
% ===========================================
end2、plotData.m
该函数是为了将数据用图表示出来。其中X = data(:, 1); y = data(:, 2);m = length(y);表示x是自变量(数据文件的第1列属性),y是预测量(第2列属性),m是样本数量。
- xlable(‘这里是横坐标’);
- ylable(‘这里是纵坐标’);
function plotData(x, y)
%PLOTDATA Plots the data points x and y into a new figure
% PLOTDATA(x,y) plots the data points and gives the figure axes labels of
% population and profit.
figure; % open a new figure window
% ====================== YOUR CODE HERE ======================
% Instructions: Plot the training data into a figure using the
% "figure" and "plot" commands. Set the axes labels using
% the "xlabel" and "ylabel" commands. Assume the
% population and revenue data have been passed in
% as the x and y arguments of this function.
%
% Hint: You can use the 'rx' option with plot to have the markers
% appear as red crosses. Furthermore, you can make the
% markers larger by using plot(..., 'rx', 'MarkerSize', 10);
plot(x,y,'rx','MarkerSize',10);
xlabel('The population of City in 10,000s');
ylabel('The profit in $10,000s');
% ============================================================
end3、computeCost.m
计算成本函数,公式如下:
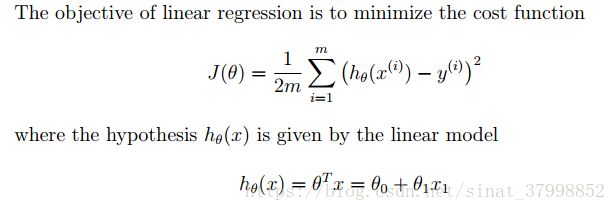
在计算过程中可以使用向量化来简化操作。
size(theta)=2*1,size(X)=m*1,所以用矩阵向量化的方式计算为:h(x)=X*theta*,同理J = 1/(2 * m) * ((h- y)’* (h- y)),
h-y得到一个m行1列的列向量,(h-y)’表示转置,与(h-y)相乘即得到对应元素相乘之和。也可以用J = 1/(2 * m) * sum ( ( (h-y ) . ^2 ) );
function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
% J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
% parameter for linear regression to fit the data points in X and y
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
% You should set J to the cost.
t = X*theta-y;
J = 1/(2*m)*(t'*t);
%或者
%J = 1/(2 * m) * sum ( ( t . ^2 ) );
% =========================================================================
end
4、gradientDescent.m
同样利用矩阵的向量化来进行计算。
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
t=1/m*(X'*(X*theta-y));
theta=theta-(alpha*t);
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end
end5、将结果可视化
这一块内容在作业里直接给出了,不需要添加代码。
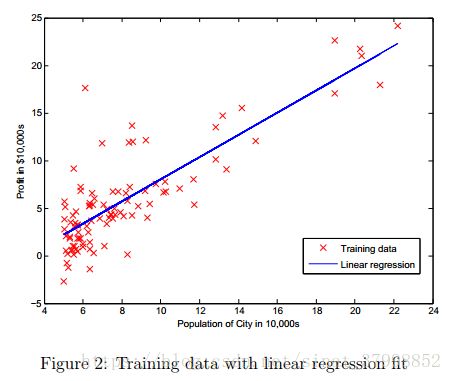
(1)可视化回归曲线:根据得到的theta来画出线性回归的曲线
% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure用结果来进行预测。如x1=[1,3.5]时,预测值predict1 = [1, 3.5] *theta,
% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf('For population = 35,000, we predict a profit of %f\n',...
predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n',...
predict2*10000);
fprintf('Program paused. Press enter to continue.\n');
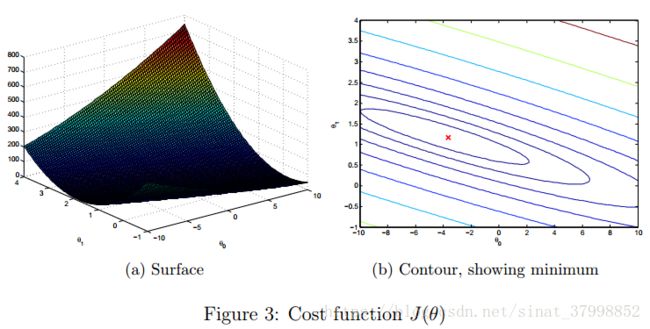
pause;(2)可视化J(theta)曲线:
%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
fprintf('Visualizing J(theta_0, theta_1) ...\n')
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));
% Fill out J_vals
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
end
end三、多元线性回归(ex1_multi.m)
1、featureNormalize.m
- 将特征进行标准化,常用的方法有均值标准化(mean normalization):
function [X_norm, mu, sigma] = featureNormalize(X)
%FEATURENORMALIZE Normalizes the features in X
% FEATURENORMALIZE(X) returns a normalized version of X where
% the mean value of each feature is 0 and the standard deviation
% is 1. This is often a good preprocessing step to do when
% working with learning algorithms.
% You need to set these values correctly
X_norm = X; %X_norm用来存放标准化之后的特征
mu = zeros(1, size(X, 2)); %mu包含每个特征属性的均值
sigma = zeros(1, size(X, 2)); %包含每个特征属性的标准差
% ====================== YOUR CODE HERE ======================
% Instructions: First, for each feature dimension, compute the mean
% of the feature and subtract it from the dataset,
% storing the mean value in mu. Next, compute the
% standard deviation of each feature and divide
% each feature by it's standard deviation, storing
% the standard deviation in sigma.
%
% Note that X is a matrix where each column is a
% feature and each row is an example. You need
% to perform the normalization separately for
% each feature.
%
% Hint: You might find the 'mean' and 'std' functions useful.
%
mu=mean(X); %均值
sigma=std(X); %标准差
X_norm=(X_norm-mu)./sigma; %特征缩放后的x=(x-均值)/标准差
% ============================================================
end
2、computeCostMulti.m
计算多元特征的成本函数,和一元的计算方法相似,是因为矩阵计算的优点。
function J = computeCostMulti(X, y, theta)
%COMPUTECOSTMULTI Compute cost for linear regression with multiple variables
% J = COMPUTECOSTMULTI(X, y, theta) computes the cost of using theta as the
% parameter for linear regression to fit the data points in X and y
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
% You should set J to the cost.
t=X*theta-y;
J=1/(2*m)*(t'*t);
% =========================================================================
end
3、gradientDescentMulti.m
多元特征的梯度下降。
function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
%GRADIENTDESCENTMULTI Performs gradient descent to learn theta
% theta = GRADIENTDESCENTMULTI(x, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCostMulti) and gradient here.
%
t=1/m*(X'*(X*theta-y));
theta=theta-(alpha*t);
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCostMulti(X, y, theta);
end
end
4、normalEqn.m用方程式法求解 θ θ
- 用方程式求解 θ θ 的过程如下:
y=θ0+θ1x1+θ2x2+...+θnxn y = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n ;
则特征向量:X=⎡⎣⎢⎢⎢x0x1...xn⎤⎦⎥⎥⎥,系数向量:θ=⎡⎣⎢⎢⎢θ0θ1...θn⎤⎦⎥⎥⎥ 特 征 向 量 : X = [ x 0 x 1 . . . x n ] , 系 数 向 量 : θ = [ θ 0 θ 1 . . . θ n ]
所以有 y=XTθ y = X T θ ,则θ=(XTX)−1X−1y θ = ( X T X ) − 1 X − 1 y
具体实现步骤为:
①为所有样本增加一个新的特征项 x0 x 0 ,且 xi0=1 x 0 i = 1 ;
得到:X=⎡⎣⎢⎢⎢x0x1...xn⎤⎦⎥⎥⎥ 得 到 : X = [ x 0 x 1 . . . x n ]②新的特te征矩阵变为
XT=[x0x1...xn]=⎡⎣⎢⎢⎢⎢11...1x11x21...xm1............x1nx2n...xmn⎤⎦⎥⎥⎥⎥ X T = [ x 0 x 1 . . . x n ] = [ 1 x 1 1 . . . x n 1 1 x 1 2 . . . x n 2 . . . . . . . . . . . . 1 x 1 m . . . x n m ]
③计算 θ θ 的公式为: θ=(XTX)−1X−1y θ = ( X T X ) − 1 X − 1 y
n=特征数量;
m=样本数量;
xi x i =第 i i 个样本;
xj x j =第 j j 个特征;
xij x j i =第 i i 个样本的第 j j 个特征;
function [theta] = normalEqn(X, y)
%NORMALEQN Computes the closed-form solution to linear regression
% NORMALEQN(X,y) computes the closed-form solution to linear
% regression using the normal equations.
theta = zeros(size(X, 2), 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Complete the code to compute the closed form solution
% to linear regression and put the result in theta.
%
% ---------------------- Sample Solution ----------------------
theta=(inv(X'*X))*X'*y;
% -------------------------------------------------------------
% ============================================================
end