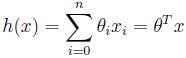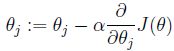批量梯度下降算法及简单Python实现

算法理论

为了实现监督学习，假设对于因变量y有自变量x1x2，则有y=θ1x1+θ2x2+θ0

θ0是偏移量，令θ0=1，得到：

我们再定义误差函数j(θ)（系数为1/2是用来消去后面的2）来表示h(x)与y的接近程度：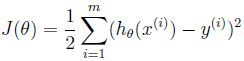

目的是使误差函数最小，需要求得使误差函数最小时的参数θ。对θ先随机初始化然后不断更新，更新算法使用梯度下降算法：

该更新公式的大致推导如下：

那么需要计算的是误差函数j(θ)的偏导：

由此可知其偏导值即为自变量矩阵与误差值乘积（注意批量训练的话有m个样本最后结果要除m，计算平均值！）

 

简单Python实现

使用一组简单的线性关系数据，员工工作年龄与薪水之间的关系：特征自变量只有一个即工作年龄，因变量为薪水。

先将数据导入Python中，得到自变量矩阵和因变量矩阵：

import numpy as np
import pandas as pd
import scipy as sp
import matplotlib.pyplot as plt
f=open("Salary_Data.csv",encoding='utf-8')
file=pd.read_csv(f)
Xi=np.array(file["YearsExperience"])
Yi=np.array(file["Salary"])
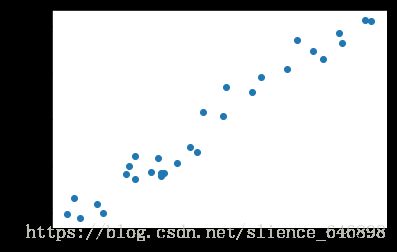
plt.scatter(Xi,Yi)
plt.show()
trainxi=np.ones((Xi.shape[0],2))//自变量矩阵是一个m*2的矩阵，m为样本数量，第一列是自变量，第二列是一个均为1的偏移量，即公式中的x0
trainxi[:,0]=Xi
trainyi=np.zeros((Yi.shape[0],1))
trainyi[:,0]=Yi

数据大体散点图，看图误差不是特别大，没有极端数据（否则一般训练集都必须先进行处理，去除一些极端值）

算法实现，定义批量梯度下降函数，x,y是训练集的变量，theta是我们要求得的参数，alpha是学习率，m为样本总数，maxx为最大迭代次数

def bgd(x,y,theta,alpha,m,maxx):
    x_trans=x.transpose()
    for i in range(0,maxx):
        hy=np.dot(x,theta)      #计算出预测的因变量结果值，m*2与2*1得到m*1的因变量矩阵
        loss=hy-y               #计算偏差值                   
        gradient=np.dot(x_trans,loss)/m  #计算当前的梯度(即偏导值)，有m个样本计算的是平均值
        theta=theta-alpha*gradient  #更新当前的theta，继续沿着梯度向下走
    return theta

定义预测函数，对得到的theta计算值与真实值的偏差

#对得到的参数θ进行预测
def predict(x,theta):
    y=np.dot(x,theta) 
    print(y)          #返回该测试得出的值，与真实值进行比较

算法迭代循环的次数也不是任意的，一般需要达到某一个要求停止循环：

1.权重的更新低于某个阈值；
2.预测的错误率低于某个阈值；
3.达到预设的最大循环次数；
其中达到任意一种，就停止算法的迭代循环，得出最终结果。

theta=np.ones((2,1))    #创建初始参数矩阵，形状行数为2（因为只有一个变量），数值初始化为1
alpha=0.01              #指定学习率
maxx=1000
theta= bgd(trainxi,trainyi,theta,alpha,Xi.shape[0],maxx)
x=np.array([[2,1],[2.9,1],[10.5,1]])   #x为测试集，简单的测试工作年龄为2、2.9、10.5的员工薪水大约应为多少钱
predict(x,theta)

得到返回结果为：

[[ 42672.78156477]
 [ 51561.26965072]
 [126619.61348763]]

大体上与真实数据接近但不够十分精确，但是最初的雏形有了。