自编码器、变分自编码器(VAE)简介以及Python实现

本篇博客简单介绍了自编码器(AutoEncoder, AE)以及近几年比较火的变分自编码器(Variational AutoEncoder, VAE)，并用Python实现。

自编码器(AE)

自编码器是一种无监督学习模型(严格来讲，说以自身为目标的监督学习，即自监督)。原始AE结构非常简单，如下图所示：

模型由输入层、隐藏层以及输出层构成，输出层神经元数目与输入层相等。
编码(encode):输入层到隐藏层，表示为$h=f(W_1^{T}x+a)$
解码(decode):隐藏层到输出层，表示为$\hat{x}=g(W_2^{T}h+b$
模型相当于对原始输入进行重构，因子训练的目的就是使重构后的$\hat{x}$与$x$之间的差异尽量小。即
当神经元取值为二进制时，目标函数为交叉熵：$$\mathcal{L}(W_1,W_2,a,b)=-\sum _{k=1}^n(x_{k}log{\hat{x}}_k+(1-x_k)log(1-{\hat{x}}_k)$$当神经元取值为任意实数时，目标函数为均方误差：$$\mathcal{L}(W_1,W_2,a,b)=\frac{1}{2}\sum _{k=1}^n||x_k-{\hat{x}}_k|{|}^2$$
自编码器的特点：

1. 仅对特定数据有效，例如用汽车图片训练的自编码器对树木图片数据无效
2. 有损压缩
3. 主要用于数据去噪以及数据降维(便于可视化)

深度自编码器

通过增加隐藏层数量，进行多层次的抽象学习，这时可采用**“逐层预训练+微调”**来训练网络。

• 逐层预训练是指通过AE来训练深度神经网络的每一层参数。具体步骤如下：
  1. 对第一个隐藏层建立AE，进行无监督训练后，删除输出层即相应参数
  2. 将第一个隐藏层输出作为输入，添加第二个隐藏层，同样构建AE并实施相同训练
  3. 重复步骤2，直至完成所有隐藏层训练
• 微调是指预训练之后还需要对网路进行监督学习训练。

稀疏自编码器

稀疏编码器与自编码器结构基本一致，区别在于隐藏层向量稀疏，即尽可能多的零元素，可以直观地理解为输入信息经稀疏编码后仅激活少量神经元。目标函数表示如下：$$\mathcal{L}(W_1,W_2,a,b)=\frac{1}{2}\sum _{k=1}^n||x_k-{\hat{x}}_k|{|}^2+\lambda \rho (h)$$式中$\rho$是稀疏性度量函数，相当于一个罚项，可采取如下三种形式：

1. 隐藏层向量L1范数，即$\rho (h)=||h|{|}_1$
2. 平均活性值，即$\rho (h_i)=\frac{1}{N}{\sum }_{k=1}^N{h}_i^k$，N为样本数
3. KL距离，KL距离通常用来度量两个分布之间的差异。我们希望隐藏层是稀疏的， 所以希望隐藏层每个神经元激活的概率${\rho }^{\ast }$比较小，例如0.05。而神经元的平均活性值$\rho (h_i)$可以看作神经元激活的概率，自然地，我们可以将$\rho (h_i)$与${\rho }^{\ast }$的距离作为罚项：$$\begin{gathered} KL({\rho }^{\ast }||\rho (h_i))={\rho }^{\ast }log\frac{{\rho }^{\ast }}{\rho (h_i)}+(1-{\rho }^{\ast })log\frac{1-{\rho }^{\ast }}{1-\rho (h_i)} \\ \rho (h)=\sum _{i=1}^{p}KL({\rho }^{\ast }||\rho (h_i)) \end{gathered}$$式中，p为隐藏层神经元数目。

变分自编码器(VAE)

咋一看VAE是变种自编码器？其实不然，变分自编码器仅仅网络结构与自编码器相似而已，原理截然不同。
自编码器将输入变量直接编码成隐藏层变量，再解码成输出变量。VAE也有“编码”(推断)和“解码”(生成)过程，但VAE将输入变量“编码”成隐变量的分布，再从隐变量分布采样，将隐变量分布“解码”成输出变量的分布。于是，网络学习目标变成使变量的分布函数逼近真实的分布函数，这个问题的求解需要采用变分方法，因而取名变分自编码器。
VAE网络示意图如下：

图中，实线表示网络计算操作，虚线表示采样操作。$\varphi$指推断网络的所有参数，$\theta$指生成网络的所有参数）

• 推断网络负责根据输入变量建立隐藏变量后验分布$q(z|x;\varphi )$
• 生成网络负责根据从从$q(z|x;\varphi )$中采样的数据，建立输出变量条件分布$p(x|z;\theta )$

模型训练的目标：
模型推断网络与生成网络的目标均是最大化证据下界$ELBO$,汇总后：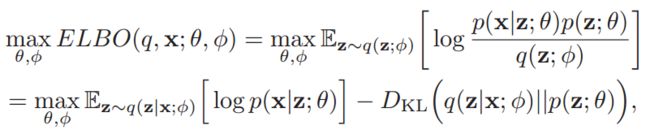
第一项期望值通常采用采样方法计算：

式中，$q(z;\varphi )$是推断网络中隐变量的先验分布，$p(z;\theta )$是生成网络中隐变量的先验分布，通常是标准正态分布。N个独立同分布样本计算目标函数：

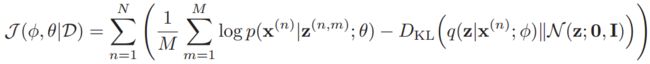
简单来说，通常假设分布函数为参数化的分布族，例如多维高斯分布。
当假设：

1. $p(z;\theta )=\mathcal{N}(z;0\text{0}0,I\text{I}I)$，即标准正态分布
2. $q(z|x;\varphi )=\mathcal{N}(z;,{\mu }_I\text{μI}{\mu }_I,{\sigma }_I^2\text{σI2}{\sigma }_I^2)$，即对角化协方差阵的正态分布，这时因为z的分量间彼此独立
3. $p(x|z;\theta )=\mathcal{N}(x;,{\mu }_G\text{μG}{\mu }_G,{\sigma }_G^2\text{σG2}{\sigma }_G^2)$
   (若变量是离散的，则表示成$p(x|z;\theta )={\Pi }_{i=1}^{d}p(x_i|z;\theta )$)

目标函数可简化为：
$$\begin{gathered} \mathcal{J}(\varphi ,\theta |x)=-||x\text{x}x-{\mu }_G\text{μG}{\mu }_G|{|}^2+D_{KL}(\mathcal{N}({\mu }_I\text{μI}{\mu }_I,{\sigma }_I\text{σI}{\sigma }_I)||\mathcal{N}(0\text{0}0,I\text{I}I)) \\ {D}_{KL}(\mathcal{N}({\mu }_I\text{μI}{\mu }_I,{\sigma }_I\text{σI}{\sigma }_I)||\mathcal{N}(0\text{0}0,I\text{I}I))=\frac{1}{2}(tr({\sigma }_I^2\text{σI2}{\sigma }_I^2+{{\mu }_I\text{μI}{\mu }_I}^T{\mu }_I\text{μI}{\mu }_I-d-log|{\sigma }_I^2\text{σI2}{\sigma }_I^2|)) \end{gathered}$$
式中，$d$为输入数据维度，第一项表示重构与输入样本之间的差距，第二项KL散度可视作罚项。
以上VAE相关图片均摘自参考资料1，详细推导请见作者书籍。

代码示例

# 自编码器
from keras.models import Model
from keras.layers import Dense, Input
from keras import regularizers
from keras.datasets import mnist

input_dim = 784
encode_dim = 32

input_layer = Input(shape=(input_dim,))
encode_layer = Dense(encode_dim, activation='relu',  # 施加稀疏限制，则构成稀疏自编码器
                     activity_regularizer=regularizers.l1(10e-5))(input_layer)
decode_layer = Dense(input_dim, activation='sigmoid')(encode_layer)

autoencoder = Model(inputs=input_layer, outputs=decode_layer)

# 根据训练后的自编码器构建编码器和解码器
encoder = Model(input_layer, encode_layer)
encoded_input = Input(shape=(encode_dim,))
decoded_output = autoencoder.layers[-1](encoded_input)
decoder = Model(encoded_input, decoded_output)

autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')

if __name__ == '__main__':
    import numpy as np

    f = np.load(r'D:\Machine_Learning\deep_learning_algorithm\autoencoder\data\mnist.npz') # 也可直接(x_train, y_train), (x_test, y_test) = mnist.load_data()
    x_train, y_train = f['x_train'], f['y_train']
    x_test, y_test = f['x_test'], f['y_test']
    f.close()
    x_train.astype(np.float) / 255
    y_train.astype(np.float) / 255
    x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))  # 将每个样本展成一维向量
    x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))
    autoencoder.fit(x_train, x_train, batch_size=256, epochs=5, shuffle=True,
                    validation_data=(x_test, x_test))

# 变分自编码器
from keras.models import Model
from keras.layers import Dense, Input, Lambda
from keras.losses import mse, binary_crossentropy
from keras.utils import plot_model
import keras.backend as K
import numpy as np


def sampling(args):
    # 再参数化采样
    z_mean, z_log_var = args
    batch = K.shape(z_mean)[0]
    dim = K.int_shape(z_mean)[1]
    epsilon = K.random_normal(shape=(batch, dim))
    return z_mean + K.exp(0.5 * z_log_var) * epsilon


def get_loss(args):
    """
    自定义损失函数
    x:原始样本
    xr: 重构样本
    m: 编码器隐变量z均值
    v: 编码器隐变量z方差的对数
    """
    x, xr, m, v = args
    dim = K.int_shape(x)[-1]
    re_loss = dim * binary_crossentropy(x, xr)  # 重构正确性度量
    kl_loss = 1 + v - K.square(m) - K.exp(v)  # d维向量，隐变量z维度为d
    kl_loss = - 0.5 * K.sum(kl_loss, axis=-1)  # kl散度，罚项
    vae_loss = K.mean(re_loss + kl_loss)
    return vae_loss


# 模型训练参数
batch_size = 128
epochs = 3

# 模型结构参数
input_dim = 784  # 输入图像为28*28
latent_dim = 2  # 潜在因子z的维度

# 构建编码器（推断网络）
inputs = Input(shape=(input_dim,))
encode_h = Dense(512, activation='relu')(inputs)
z_mean = Dense(latent_dim, activation='relu')(encode_h)
z_log_var = Dense(latent_dim, activation='relu')(encode_h)  # log(sigma^2)
z_sample = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])  # 采样
encoder = Model(inputs, [z_mean, z_log_var, z_sample])  # 编码器输出结果为3层

# 构建解码器（生成网络）
inputs_decoder = Input(shape=(latent_dim,))
decode_h = Dense(512, activation='relu')(inputs_decoder)
x_mean_decoded = Dense(input_dim, activation='sigmoid')(decode_h)
decoder = Model(inputs_decoder, x_mean_decoded)

# 构建VAE模型
x_decoded = decoder(encoder(inputs)[2])
outputs = Lambda(get_loss)([inputs, x_decoded, z_mean, z_log_var])  # 模型直接输出损失函数值

vae_model = Model(inputs, outputs)
vae_model.compile(optimizer='adam', loss=lambda y_true, y_pred: y_pred)

if __name__ == '__main__':
    # plot_model(vae_model, show_shapes=True)
    f = np.load(r'D:\Machine_Learning\deep_learning_algorithm\autoencoder\data\mnist.npz')
    x_train, y_train = f['x_train'], f['y_train']
    x_test, y_test = f['x_test'], f['y_test']
    f.close()
    x_train = np.reshape(x_train, [-1, input_dim])
    x_test = np.reshape(x_test, [-1, input_dim])
    x_train = x_train.astype('float32') / 255
    x_test = x_test.astype('float32') / 255
    vae_model.fit(x_train, x_train, shuffle=True, epochs=epochs, batch_size=batch_size)

    encoded_imgs = encoder.predict(x_test)[2]
    decoded_imgs = decoder.predict(encoded_imgs)


    def plot_img(x_test, decoded_imgs):
        # 对比重构前后的图像
        import matplotlib.pyplot as plt

        n = 10
        plt.figure(figsize=(20, 4))
        for i in range(n):
            # 展示原始图像
            ax = plt.subplot(2, n, i + 1)
            plt.imshow(x_test[i].reshape(28, 28))
            plt.gray()
            ax.get_xaxis().set_visible(False)
            ax.get_yaxis().set_visible(False)
            # 展示重构后图像
            ax = plt.subplot(2, n, i + 1 + n)
            plt.imshow(decoded_imgs[i].reshape(28, 28))
            plt.gray()
            ax.get_xaxis().set_visible(False)
            ax.get_yaxis().set_visible(False)
        plt.show()
        return


    plot_img(x_test, decoded_imgs)

注：本代码是对参考资料2中的代码进行部分修改而成，网络未经过训练。

参考资料

1. 邱锡鹏《神经网络与深度学习》
2. Building Autoencoders in Keras

注：如有不当之处，请指正。