OpenCV学习笔记（十六）角点检测

角点检测：

图像像素区域的兴趣点区域对于目标检测/目标跟踪有着重要的意义。当兴趣点周围存在方形区域时，最易形成角点。对于兴趣点检测，角点反应的是图像中局部最大值或者最小值的孤立点，可理解为 区域领域的小方块，存在于不同方向的主边缘处。窗口向任意方向的移动都会导致图像灰度的明显变换，形成的点集称为角点。

1. moravec角点

moravec角点是最早的角点检测算法之一，常用于立体匹配。moravec角点的原理是通过滑动窗口像素变化来实现角点检测，首先计算窗口像素的兴趣值，即以当前像素为中心像素点，取一个正方形窗口wxw，计算0°，45°，90°，135°四个方向灰度差的平方和，取其中的最小值作为兴趣像素点的兴趣值。

moravec角点检测器对每一个兴趣中心点进行划窗遍历，计算其相关8-领域方向的特征关系，窗口的变化可以取3x3,5x5,7x7。moravec角点检测与其他同类型角点检测相比有不足之处。

(1)非均匀性响应。很容易受到邻近特性的影响，一般在实验前，先进行平滑处理操作。moravec对45°响应很强，这是因为只考虑了每隔45°的方向变化，而没有在全部方向上。

(2)噪声响应。由于窗口函数是一个二值函数，不管像素点离中心点的距离是多少，均赋予一样的权重，致使其对应的噪声也有很强的响应。一般在进行角点检测前，先对图像兴趣区域采用较大的窗口或者先进行平滑操作。

程序体现：

#include 
#include 
#include 
#include 
#include 
using namespace cv;
using namespace std;
Mat MoravecCorners(Mat srcImage, int kSize, int threshold)
{
	Mat resMorMat = srcImage.clone();
	//获取初始化参数信息
	int r = kSize / 2;
	const int nRows = srcImage.rows;
	const int nCols = srcImage.cols;
	int nCount = 0;
	CvPoint *pPoint = new CvPoint[nRows * nCols];
	//图像遍历
	for (int i = r; i < srcImage.rows - r; i++)
	{
		for (int j = r; j < srcImage.cols - r; j++)
		{
			int wV1, wV2, wV3, wV4;
			wV1 = wV2 = wV3 = wV4 = 0;
			//计算水平方向窗内的兴趣值
			for (int k = -r; k < r; k++)
				wV1 += (srcImage.at(i, j + k) - srcImage.at(i, j + k + 1))*
				(srcImage.at(i, j + k) - srcImage.at(i, j + k + 1));
			//计算垂直方向窗内的兴趣值
			for (int k = -r; k < r; k++)
				wV2 += (srcImage.at(i + k, j) - srcImage.at(i + k + 1, j))*
				(srcImage.at(i + k, j) - srcImage.at(i + k + 1, j));
			//计算45方向窗内兴趣值
			for (int k = -r; k < r; k++)
				wV3 += (srcImage.at(i + k, j + k) - srcImage.at(i + k + 1, j + k + 1))*
				(srcImage.at(i + k, j + k) - srcImage.at(i + k + 1, j + k + 1));
			//计算135方向窗内的兴趣值
			for (int k = -r; k < r; k++)
				wV3 += (srcImage.at(i + k, j - k) - srcImage.at(i + k + 1, j - k - 1))*
				(srcImage.at(i + k, j - k) - srcImage.at(i + k + 1, j - k - 1));
			//选取其中的最小值作为该像素点的最终兴趣值
			int value = min(min(wV1, wV2), min(wV3, wV4));
			//若兴趣值大于阈值，则将点的坐标存入数组中
			if (value > threshold)
			{
				pPoint[nCount] = cvPoint(j, i);
				nCount++;
			}
		}
	}
	//绘制兴趣点
	for (int i = 0; i < nCount; i++)
		circle(resMorMat, pPoint[i], 5, Scalar(255, 255, 255), 1, 8, 0);
	return resMorMat;
}
int main()
{
	Mat srcImage = imread("D:\\Projects\\4.jpg");
	if (!srcImage.data)
		return -1;
	Mat srcGray;
	cvtColor(srcImage, srcGray, CV_BGR2GRAY);
	Mat resMorMat = MoravecCorners(srcGray, 5, 10000);
	imshow("srcImage", srcImage);
	imshow("resMorMat", resMorMat);
	waitKey(0);
	return 0;
}

2. harris角点

harris角点在moravec角点的基础上进行了改进，对比moravec角点的连续平方求和，它引入了局部变化因子，利用高斯权重函数进行角点检测。

将实对称矩阵对角化处理后，对应项可以理解为旋转因子，经过对角化处理后，根据两个正交方向的变化分量计算其相应的特征值。如果两个特征值均较大且数值相当，则图像窗口在所有方向上的移动都将产生明显的灰度变化，可判断其将形成角点。如果仅有一个特征值较高且远远大于另一特征值，则可以得到相应边缘，其他情况下可以得到稳定区域。基于上述特征值特性，harris角点理论提出了相应的角点相应函数

C(i,j)=det(M)-k(trace(M))x(trace(M));     M是2x2的局部结构矩阵。k是常量因子，通常情况取值为0.04~0.06；对图像窗口内数据进行求和加权，实际上可以更好地刻画窗口中心特性。harris角点检测器还是目前应用最广泛的角点检测器之一，它检测率高，且可得到重复响应。harris角点检测算法的实现步骤：

(1) 利用水平与竖直差分算子对图像进行卷积操作，然后根据实对称矩阵M的组成，计算对应矩阵元素的值。

(2) 利用高斯函数对矩阵M进行平滑操作，得到新的M矩阵，步骤1和步骤2可以交换顺序，也可先对图像进行高斯滤波，再求相应方向上的梯度大小。

(3) 对每一像素和给定的领域窗口，计算局部特征结果矩阵M的特征值和相应的函数

C(i,j)=det(M)-k(trace(M))x(trace(M));  

(4) 选取响应函数C的阈值，根据非极大值抑制原理，同时满足阈值及某领域内的局部极大值为候选角点。

利用cornerHarris()函数实现harris角点检测：

void cornerHarris(InputArray src, OutputArray dst, int blockSize, int apertureSize, double k, int borderType=BORDER_DEFAULT )

• src – Input single-channel 8-bit or floating-point image.
• dst – Image to store the Harris detector responses. It has the type CV_32FC1 and the same size as src .
• blockSize – Neighborhood size (see the details on cornerEigenValsAndVecs() ).
• apertureSize – Aperture parameter for the Sobel() operator.
• k – Harris detector free parameter. See the formula below.     公式中的k值
• boderType – Pixel extrapolation method. See borderInterpolate() 

程序实现：

#include 
#include 
#include 
#include 
using namespace cv;
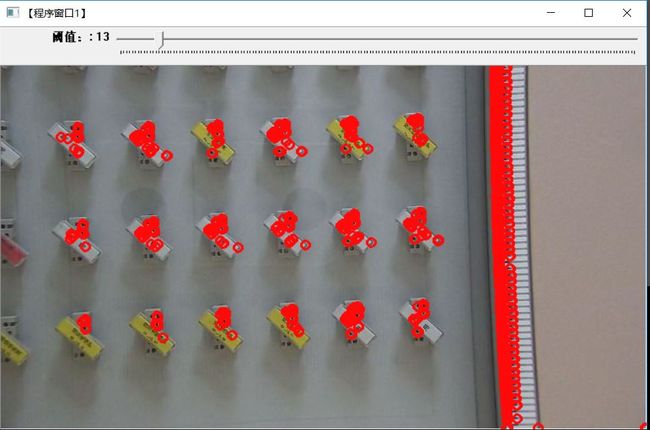
#define WINDOW_NAME1 "【程序窗口1】"
#define WINDOW_NAME2 "【程序窗口2】"
Mat g_srcImage, g_srcImage1, g_grayImage;
int thresh = 30;
int max_thresh = 175;
void on_CornerHarris(int, void*);
int main()
{
	g_srcImage = imread("D:\\Projects\\3.jpg");
	if (!g_srcImage.data)
		return -1;
	imshow("g_srcImage", g_srcImage);
	g_srcImage1 = g_srcImage.clone();
	cvtColor(g_srcImage1, g_grayImage, COLOR_BGR2GRAY);
	namedWindow(WINDOW_NAME1, WINDOW_AUTOSIZE);
	createTrackbar("阈值：", WINDOW_NAME1, &thresh, max_thresh, on_CornerHarris);
	on_CornerHarris(0, 0);
	waitKey(0);
	return 0;
}
void on_CornerHarris(int, void*)
{
	Mat dstImage;
	Mat normImage;
	Mat scaledImage;
	dstImage = Mat::zeros(g_srcImage.size(), CV_32FC1);
	g_srcImage1 = g_srcImage.clone();
	//进行角点检测
	cornerHarris(g_grayImage, dstImage, 2, 3, 0.04, BORDER_DEFAULT);
	//归一化与转换
	normalize(dstImage, normImage, 0, 255, NORM_MINMAX, CV_32FC1);
	convertScaleAbs(normImage, scaledImage);
	for (int j = 0; j < normImage.rows; j++)
	{
		for (int i = 0; i(j, i)>thresh + 80)
			{
				circle(g_srcImage1, Point(i, j), 5, Scalar(10, 10, 255), 2, 8, 0);
				circle(scaledImage, Point(i, j), 5, Scalar(0, 10, 255), 2, 8, 0);
			}
		}
			
	}
	imshow(WINDOW_NAME1, g_srcImage1);
	imshow(WINDOW_NAME2, scaledImage);
}

效果图：

3. Shi-Tomasi角点

a,b分别是M矩阵的两个特征值，Shi-Tomasi角点检测则选取了不同的角点响应函数，C(i,j)=min(a,b)；

Shi-Tomasi角点检测划分相关一对一匹配对，依据图像的角点特征，图像灰度和位置信息，采用最大互相函数进行相似度计算，最终实现角点检测。OpenCV中利用goodFeaturesToTrack()实现角点检测算法。

void goodFeaturesToTrack(InputArray image, OutputArray corners, int maxCorners, double qualityLevel, double minDistance, InputArray mask=noArray(), int blockSize=3, bool useHarrisDetector=false, double k=0.04 )

• image – Input 8-bit or floating-point 32-bit, single-channel image.
• corners – Output vector of detected corners.
• maxCorners – Maximum number of corners to return. If there are more corners than are found, the strongest of them is returned.
• qualityLevel – Parameter characterizing the minimal accepted quality of image corners. The parameter value is multiplied by the best corner quality measure, which is the minimal eigenvalue (see cornerMinEigenVal() ) or the Harris function response (see cornerHarris()). The corners with the quality measure less than the product are rejected. For example, if the best corner has the quality measure = 1500, and the qualityLevel=0.01 , then all the corners with the quality measure less than 15 are rejected.
• minDistance – Minimum possible Euclidean distance between the returned corners.      取0.01
• mask – Optional region of interest. If the image is not empty (it needs to have the type CV_8UC1 and the same size as image ), it specifies the region in which the corners are detected.    Mat()
• blockSize – Size of an average block for computing a derivative covariation matrix over each pixel neighborhood. SeecornerEigenValsAndVecs() .      3
• useHarrisDetector – Parameter indicating whether to use a Harris detector (see cornerHarris()) or cornerMinEigenVal(). false
• k – Free parameter of the Harris detector.     0.04

程序实现：

#include 
#include 
#include 
using namespace cv;
using namespace std;
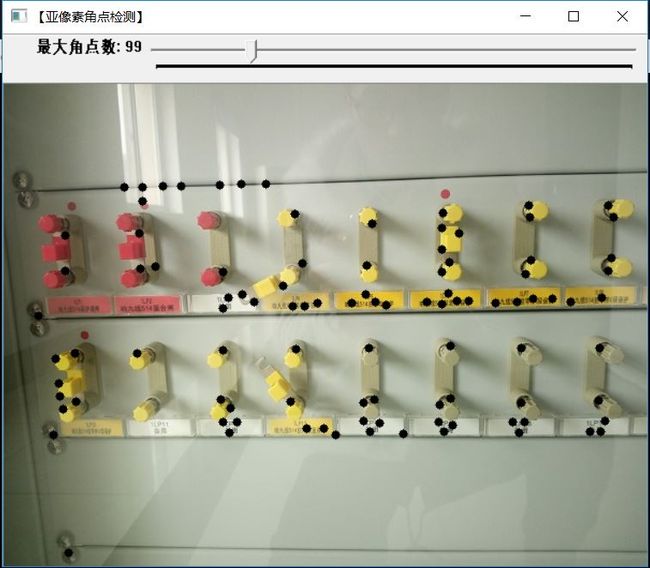
#define WINDOW_NAME "【亚像素角点检测】"
Mat g_srcImage, g_grayImage;
int g_maxCornerNumber = 33;
int g_maxTrackbarNumber = 500;
RNG g_rng(12345);
void on_GoodFeaturesToTrack(int, void*)
{
	if (g_maxCornerNumber <= 1)
	{
		g_maxCornerNumber = 1;
	}
	vector corners;
	double qualityLevel = 0.01;
	double minDistance = 10;
	int blockSize = 3;
	double k = 0.04;
	Mat copy = g_srcImage.clone();
	goodFeaturesToTrack(g_grayImage, corners, g_maxCornerNumber, qualityLevel, minDistance, Mat(), blockSize, false, k);
	int r = 4;
	for (unsigned int i = 0; i < corners.size(); i++)
	{
		circle(copy, corners[i], r, Scalar(0,0,0),
			-1, 8, 0);
	}
	imshow(WINDOW_NAME, copy);
	
}
int main()
{
	g_srcImage = imread("D:\\Projects\\6.jpg");
	if (!g_srcImage.data)
		return -1;
	cvtColor(g_srcImage, g_grayImage, COLOR_BGR2GRAY);
	namedWindow(WINDOW_NAME, WINDOW_AUTOSIZE);
	createTrackbar("最大角点数", WINDOW_NAME, &g_maxCornerNumber, g_maxTrackbarNumber, on_GoodFeaturesToTrack);
	on_GoodFeaturesToTrack(0, 0);
	waitKey(0);
	return 0;
}

显示结果：