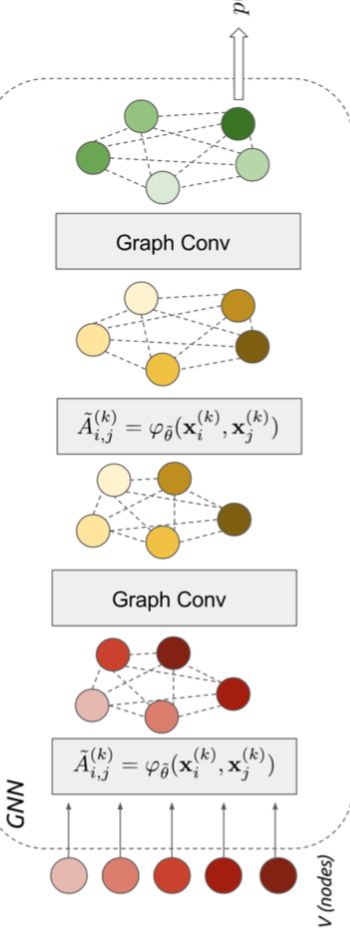
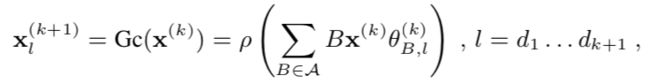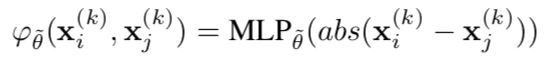- 女儿考研完报考雅思
捡拾流年
是否我过于焦虑?会不会无形间让女儿觉得压力太大了啊。2022年对于我们家来说是不平常的一年。女儿今年大四,为了准备考研,暑假也没回家,年初去了学校到了年末才回家。女儿自己一个人面对考研,没有参加培训,大四学校作业论文等课业也多,她同时也是很努力复习考研的。在疫情开放很多羊的时期,女儿终于顺顺利利参加12月24、25号的考研,我们和家人都觉得女儿回家来要好好休息调养。可女儿回到家,我再查阅考研信息,
- 绝招曝光!3小时高效利用ChatGPT写出精彩论文
kkai人工智能
chatgpt人工智能ai学习媒体
在这份指南中,我将深入解析如何利用ChatGPT4.0的高级功能,指导整个学术研究和写作过程。从初步探索研究主题,到撰写结构严谨的学术论文,我将一步步展示如何在每个环节中有效运用ChatGPT。如果您还未使用PLUS版本,可以参考相关教程。**初步探索与主题的确定**起初,我处于庞大的知识领域中,寻找一个可深入研究的领域。ChatGPT如同灯塔,通过深入分析最新研究趋势和领域热点,帮助我在广阔的学
- 自动写论文的网站推荐这5款实用类工具
小猪包333
写论文人工智能深度学习计算机视觉AI写作
在当今学术研究和写作领域,AI论文写作工具的出现极大地提高了写作效率和质量。这些工具不仅能够帮助研究人员快速生成论文草稿,还能进行内容优化、查重和排版等操作。以下是五款实用类工具推荐,特别是千笔-AIPassPaper。1.千笔-AIPassPaper千笔-AIPassPaper是一款功能强大且全面的AI论文写作助手,用户只需输入基本的研究需求和关键词,便能迅速生成一篇完整的论文。该工具利用先进的
- 推荐3家毕业AI论文可五分钟一键生成!文末附免费教程!
小猪包333
写论文人工智能AI写作深度学习计算机视觉
在当前的学术研究和写作领域,AI论文生成器已经成为许多研究人员和学生的重要工具。这些工具不仅能够帮助用户快速生成高质量的论文内容,还能进行内容优化、查重和排版等操作。以下是三款值得推荐的AI论文生成器:千笔-AIPassPaper、懒人论文以及AIPaperPass。千笔-AIPassPaper千笔-AIPassPaper是一款基于深度学习和自然语言处理技术的AI写作助手,旨在帮助用户快速生成高质
- 4款毕业论文参考文献格式生成器(附加详细步骤)
小猪包333
写论文人工智能深度学习计算机视觉AI写作
在撰写毕业论文时,参考文献的格式规范是至关重要的。为了帮助学生和学者们更高效地生成符合要求的参考文献格式,本文将详细介绍四款推荐的参考文献格式生成器,并提供详细的使用步骤。1.千笔-AIPassPaper千笔-AIPassPaper是一款先进的AI辅助论文写作工具,不仅能够自动生成大纲、开题报告,还能一键生成参考文献。AI论文,免费大纲,10分钟3万字https://www.aipaperpass
- AI论文写作推荐哪个好?分享5款AI论文写作带数据图表网站
小猪包333
写论文人工智能深度学习计算机视觉
在当今学术研究和写作领域,AI论文写作工具的出现极大地提高了写作效率和质量。这些工具不仅能够帮助研究人员快速生成论文草稿,还能进行内容优化、查重和排版等操作。以下是五款推荐的AI论文写作工具,包括千笔-AIPassPaper。千笔-AIPassPaper千笔-AIPassPaper是一款功能强大的AI论文写作助手,旨在帮助用户快速生成高质量的论文内容。AI论文,免费大纲,10分钟3万字https:
- AI论文题目生成器怎么用?9款论文写作网站简单3步搞定
小猪包333
写论文人工智能深度学习计算机视觉
在当今信息爆炸的时代,AI写作工具的出现极大地提高了写作效率和质量。本文将详细介绍9款优秀的论文写作网站,并重点推荐千笔-AIPassPaper。一、千笔-AIPassPaper千笔-AIPassPaper是一款功能强大的AI论文生成器,基于最新的自然语言处理技术,能够一键生成高质量的毕业论文、开题报告等文本内容。它不仅提供智能选题、文献推荐和论文润色等功能,还具有较高的用户评价。其文献综述生成功
- 毕业论文附录一般都写什么?大学生写论文是干嘛用的
写个原创论文
人工智能深度学习AI写作chatgpt论文阅读
毕业论文的附录通常包含一些在正文中不便于展示或详细阐述的内容,但对理解论文整体又具有重要意义的资料。具体来说,附录可能包含以下内容:AI论文,免费大纲,10分钟3万字,查重高于15%退费,支持数据图表!!AIPaperPass-AI论文写作指导平台AIPaperPass是AI原创论文写作平台,免费千字大纲,5分钟生成3万字初稿,提供答辩汇报ppt、开题报告、任务书等,40篇真实中英文知网参考文献,
- 【加密算法基础——RSA 加密】
XWWW668899
网络服务器笔记python
RSA加密RSA(Rivest-Shamir-Adleman)加密是非对称加密,一种广泛使用的公钥加密算法,主要用于安全数据传输。公钥用于加密,私钥用于解密。RSA加密算法的名称来源于其三位发明者的姓氏:R:RonRivestS:AdiShamirA:LeonardAdleman这三位计算机科学家在1977年共同提出了这一算法,并发表了相关论文。他们的工作为公钥加密的基础奠定了重要基础,使得安全通
- 《拖延心理学》(一)你为什么会拖延?|木盒笔记
纯se蓝调
《拖延心理学》是帮助你向拖延症宣战的一本书,作者简·博克和莱诺拉·袁是全球知名的拖延症治疗专家。大概每个人或多或少总会有一点拖延症的行为。比如明天要叫论文了,今天你还没有写好,你一边在焦虑症怎么办,一边又拿着手机漫无目的的刷新闻;比如你想了很久准备减肥,但是迟迟又没有行动,想着今天晚上少吃一点吧、明天我就开始运动。今天分析的笔记来告诉你“你为什么会拖延?”,解读人杨坚。有人说拖延就像巨大的泥沼,让
- 2024年华为杯数学建模研赛C题思路代码+论文助攻
DS数模
2024华为杯数学建模华为2024华为杯2024研究生数学建模2024研赛
2024年华为杯研究生数学建模竞赛(以下简研赛)将于9月21日上午8时正式开始。下文包含:2024研赛思路解析、研赛参赛时间及规则信息说明、好用的数模技巧及如何备战数学建模竞赛C君将会第一时间发布选题建议、所有题目的思路解析、相关代码、参考文献、参考论文等多项资料,帮助大家取得好成绩。2024年研赛将于9月21日上午8时正式开始这里有些资料,大家可以看看:【2024最全国赛研赛数模资料包】C君珍贵
- 轻量级模型解读——轻量transformer系列
lishanlu136
#图像分类轻量级模型transformer图像分类
先占坑,持续更新。。。文章目录1、DeiT2、ConViT3、Mobile-Former4、MobileViTTransformer是2017谷歌提出的一篇论文,最早应用于NLP领域的机器翻译工作,Transformer解读,但随着2020年DETR和ViT的出现(DETR解读,ViT解读),其在视觉领域的应用也如雨后春笋般渐渐出现,其特有的全局注意力机制给图像识别领域带来了重要参考。但是tran
- 基于JavaWeb开发的Java+SpringMvc+vue+element实现上海汽车博物馆平台
网顺技术团队
成品程序项目javavue.js汽车课程设计springboot
基于JavaWeb开发的Java+SpringMvc+vue+element实现上海汽车博物馆平台作者主页网顺技术团队欢迎点赞收藏⭐留言文末获取源码联系方式查看下方微信号获取联系方式承接各种定制系统精彩系列推荐精彩专栏推荐订阅不然下次找不到哟Java毕设项目精品实战案例《1000套》感兴趣的可以先收藏起来,还有大家在毕设选题,项目以及论文编写等相关问题都可以给我留言咨询,希望帮助更多的人文章目录基
- 深度学习-点击率预估-研究论文2024-09-14速读
sp_fyf_2024
深度学习人工智能
深度学习-点击率预估-研究论文2024-09-14速读1.DeepTargetSessionInterestNetworkforClick-ThroughRatePredictionHZhong,JMa,XDuan,SGu,JYao-2024InternationalJointConferenceonNeuralNetworks,2024深度目标会话兴趣网络用于点击率预测摘要:这篇文章提出了一种新
- 推荐开源项目:Zotero引用计数管理器——学术研究的智能助手
蔡鸿烈Hope
推荐开源项目:Zotero引用计数管理器——学术研究的智能助手zotero-citationcountsZoteropluginforauto-fetchingcitationcountsfromvarioussources项目地址:https://gitcode.com/gh_mirrors/zo/zotero-citationcounts项目介绍在学术界,每篇论文背后都承载着学者们辛勤的研究成
- overleaf如何下载论文的pdf
风也温柔☆
overleafpdfoverleaf
用overleaf写完英文论文后,要将论文保存为PDF格式点击图片中的下载按钮然后选择一个路径保存论文的PDF格式即可。
- 通过与AI代理结对编程在集成课程中促进AI辅助学习循环的方法
神一样的老师
论文阅读分享人工智能结对编程学习
本篇论文提出了一种新的方法论,利用人工智能(AI)技术的最新进展,为学生制定一个AI辅助的代码学习循环。这种方法在现有的学习过程中创新性地融入了结对编程,以增强学生的互动式学习体验。以下是论文的主要内容概述:摘要(Abstract):提出了一种新方法,利用AI技术来辅助学生学习编程。方法包括将示例代码转化为脚手架代码作为练习,通过教师与AI的配对来实现。脚手架代码作为学生在硬件平台上迭代完成和调试
- 系统架构师软考历年论文题目(2009-2024年)及分析
pccai-vip
系统架构师系统架构
时间题目20091.论基于DSSA的软件架构设计与应用;2.论信息系统建模方法;3.论基于REST服务的Web应用系统设计;4.论软件可靠性设计与应用20101.论软件的静态演化和动态演化及其应用;2.论数据挖掘技术的应用;3.论大规模分布式系统缓存设计策略;4.论软件可靠性评价20111.论模型驱动架构在系统开发中的应用;2.论企业集成平台的架构设计;3.论企业架构管理与应用;4.论软件需求获取
- 吾日三省吾身:DAY4
眼前一亮
做得好的三件事:开车去机场接亲戚,没让老婆跑受累,并且开车前去校验了车,降低了开车风险;看了一小会论文,虽然时间很短;陪小孩玩了一会,发现小孩子的想象力很好。做得不好的三件事:没有看书学习;没有健身运动,没给家人打个电话。
- 【每日精进】务必开始第三战役
金台望道
9月3日星期六天气:晴早晨:6点才起,完成早起事务;考虑本月计划。2022年还剩下4个月,务必完成我的三大战役之三《网络空间社会思潮批判》;今年的小说务必要安排时间修改完。——这是业余主要做的事。另外,近期《讲话与丁玲的创作》、瑞金会议的征文,也还要做的。此后与主要事务无关的论文就不再写了。——这四个月,要注意修改好已有的论文并投稿发表。以后这件事要提到议事日程上来。这都是在教学事务之外的工作。幸
- 【读书清单】硅谷钢铁侠
馋人小博
1.出生在南非埃隆马斯克,出生在南非,自幼总是因为思考而陷入发呆的状态;他对读书如饥似渴,每天可以花上10个小时看书,甚至将两套百科全书读得烂熟于心。十二岁就设计了名为“炸弹”的游戏源代码。这大概就是我们嘴里的“别人家的孩子”2.挺进加拿大父母离异,17岁的马斯克被允许母亲的加拿大国际,他毫不犹豫的离开了南非,再也没回去过。在加拿大,他上了大学,遇见爱情,之后转学,转学后的论文让教授眼前一亮。3.
- 【笔记】扩散模型(七):Latent Diffusion Models(Stable Diffusion)论文解读与代码实现
LittleNyima
DiffusionModels笔记stablediffusionAIGC人工智能
论文链接:High-ResolutionImageSynthesiswithLatentDiffusionModels官方实现:CompVis/latent-diffusion、CompVis/stable-diffusion这一篇文章的内容是LatentDiffusionModels(LDM),也就是大名鼎鼎的StableDiffusion。先前的扩散模型一直面临的比较大的问题是采样空间太大,学
- 论文分享系列(三)——论软件架构风格
马斯洛金字塔下的小灵猴儿
#软考高项架构师论软件架构风格论文
论软件架构风格摘要2023年5月,我司启动了精彩购电商系统的开发工作,该项目组中我担任系统架构师岗位,主要负责整体架构设计与中间件选型。本文以该电商平台为例,主要讨论了软件架构风格在该项目中的具体应用。整个系统采用具有三层的层次式软件架构的设计思想,分别是应用层,服务层,数据层。在应用层中的业务逻辑层的设计中,将整个业务系统划分为十余个子系统。服务层以springcloud服务框架为核心,数据采用
- 论文分享系列(二)——论微服务架构及其应用
马斯洛金字塔下的小灵猴儿
#软考高项架构师论微服务架构及其应用论文
论微服务架构及其应用摘要2023年5月,我司启动了精彩购电商系统的开发工作,该项目组中我担任系统架构师岗位,主要负责整体架构设计与中间件选型。本文以该电商平台为例,将介绍微服务架构的特点、应用场景以及实现方法。系统以SpringCloud微服务框架开发,分为前端Web服务、平台保障服务、业务服务三部分。前端Web服务由负载均衡与服务器集群结合,实现高并发的前台界面;平台保障服务以Eureka为中心
- 《心理治疗师的刻意练习》读后记
海涛心理咨询
读后记:这本书主要是写一位心理咨询师从小白到合格咨询师的刻意练习。开篇写了自己初做心理咨询师的美好体验与尴尬——50%的来访者没有变好(而这居然是行业平均水平);希望自己的咨询水平能够提高而查阅了相关论文,请教了相关专家,开始了刻意练习之路;刻意练习如何降低了自己的焦虑,最终提高了自己的咨询表现,并且要和读者分享自己的成功之路。书中也提供了一些科学研究和统计调查:资深咨询师的来访者反馈与新手咨询师
- 基于springboot+vue的“考研资讯平台”程序设计实现【毕业论文,源码】
一枚务实的码农
毕业设计毕设考研springboot毕业论文系统源码
摘要随着现在网络的快速发展,网络的应用在各行各业当中它很快融入到了许多学校的眼球之中,他们利用网络来做这个电商的服务,随之就产生了“考研资讯平台”,这样就让学生考研资讯平台更加方便简单。对于本考研资讯平台的设计来说,它主要是采用java技术。在整个系统的设计当中它是应用mysql数据库来完成的,具体根据网上考研资讯平台的现状来进行开发的,具体根据学生需求实现网上考研资讯平台网络化的管理,各类信息有
- HBase介绍
mingyu1016
数据库
概述HBase是一个分布式的、面向列的开源数据库,源于google的一篇论文《bigtable:一个结构化数据的分布式存储系统》。HBase是GoogleBigtable的开源实现,它利用HadoopHDFS作为其文件存储系统,利用HadoopMapReduce来处理HBase中的海量数据,利用Zookeeper作为协同服务。HBase的表结构HBase以表的形式存储数据。表有行和列组成。列划分为
- 基于nodejs+vue的美妆彩妆网站的设计与实现(源码+LW+调试文档+讲解等)
程序员gelei
nodejs毕业设计项目vue.js前端javascript
目录:博主介绍:完整视频演示:系统技术介绍:后端Java介绍前端框架Vue介绍具体功能截图:部分代码参考:Mysql表设计参考:项目测试:项目论文:为什么选择我:源码获取:博主介绍:博主:程序员gelei:全网拥有20W+粉丝、CSDN作者、博客专家、全栈领域优质创作者、平台优质Java创作者、专注于Java、小程序、python、安卓技术领域和毕业项目实战✌Java精品实战案例《1000套》20
- 基于django+vue代驾管理系统【开题报告+程序+论文】-计算机毕设
zhjie102
djangovue.js课程设计
本系统(程序+源码+数据库+调试部署+开发环境)带论文文档1万字以上,文末可获取,系统界面在最后面。系统程序文件列表开题报告内容研究背景随着城市化进程的加速和人们生活水平的提高,私家车数量急剧增加,但随之而来的酒驾问题也日益严峻,严重威胁着道路交通安全与公众生命财产安全。为了有效遏制酒驾行为,代驾服务应运而生并迅速普及。然而,当前市场上的代驾服务大多依赖于电话预约、人工调度等传统方式,存在效率低下
- python毕业设计作品:python闲置物品二手交易平台系统设计与实现毕业设计源代码(Django框架)
黄菊华老师
毕设资料python二手交易平台系统
博主介绍:黄菊华老师《Vue.js入门与商城开发实战》《微信小程序商城开发》图书作者,CSDN博客专家,在线教育专家,CSDN钻石讲师;专注大学生毕业设计教育和辅导。所有项目都配有从入门到精通的基础知识视频课程,学习后应对毕业设计答辩。项目配有对应开发文档、开题报告、任务书、PPT、论文模版等项目都录了发布和功能操作演示视频;项目的界面和功能都可以定制,包安装运行!!!如果需要联系我,可以在CSD
- 集合框架
天子之骄
java数据结构集合框架
集合框架
集合框架可以理解为一个容器,该容器主要指映射(map)、集合(set)、数组(array)和列表(list)等抽象数据结构。
从本质上来说,Java集合框架的主要组成是用来操作对象的接口。不同接口描述不同的数据类型。
简单介绍:
Collection接口是最基本的接口,它定义了List和Set,List又定义了LinkLi
- Table Driven(表驱动)方法实例
bijian1013
javaenumTable Driven表驱动
实例一:
/**
* 驾驶人年龄段
* 保险行业,会对驾驶人的年龄做年龄段的区分判断
* 驾驶人年龄段:01-[18,25);02-[25,30);03-[30-35);04-[35,40);05-[40,45);06-[45,50);07-[50-55);08-[55,+∞)
*/
public class AgePeriodTest {
//if...el
- Jquery 总结
cuishikuan
javajqueryAjaxWebjquery方法
1.$.trim方法用于移除字符串头部和尾部多余的空格。如:$.trim(' Hello ') // Hello2.$.contains方法返回一个布尔值,表示某个DOM元素(第二个参数)是否为另一个DOM元素(第一个参数)的下级元素。如:$.contains(document.documentElement, document.body); 3.$
- 面向对象概念的提出
麦田的设计者
java面向对象面向过程
面向对象中,一切都是由对象展开的,组织代码,封装数据。
在台湾面向对象被翻译为了面向物件编程,这充分说明了,这种编程强调实体。
下面就结合编程语言的发展史,聊一聊面向过程和面向对象。
c语言由贝尔实
- linux网口绑定
被触发
linux
刚在一台IBM Xserver服务器上装了RedHat Linux Enterprise AS 4,为了提高网络的可靠性配置双网卡绑定。
一、环境描述
我的RedHat Linux Enterprise AS 4安装双口的Intel千兆网卡,通过ifconfig -a命令看到eth0和eth1两张网卡。
二、双网卡绑定步骤:
2.1 修改/etc/sysconfig/network
- XML基础语法
肆无忌惮_
xml
一、什么是XML?
XML全称是Extensible Markup Language,可扩展标记语言。很类似HTML。XML的目的是传输数据而非显示数据。XML的标签没有被预定义,你需要自行定义标签。XML被设计为具有自我描述性。是W3C的推荐标准。
二、为什么学习XML?
用来解决程序间数据传输的格式问题
做配置文件
充当小型数据库
三、XML与HTM
- 为网页添加自己喜欢的字体
知了ing
字体 秒表 css
@font-face {
font-family: miaobiao;//定义字体名字
font-style: normal;
font-weight: 400;
src: url('font/DS-DIGI-e.eot');//字体文件
}
使用:
<label style="font-size:18px;font-famil
- redis范围查询应用-查找IP所在城市
矮蛋蛋
redis
原文地址:
http://www.tuicool.com/articles/BrURbqV
需求
根据IP找到对应的城市
原来的解决方案
oracle表(ip_country):
查询IP对应的城市:
1.把a.b.c.d这样格式的IP转为一个数字,例如为把210.21.224.34转为3524648994
2. select city from ip_
- 输入两个整数, 计算百分比
alleni123
java
public static String getPercent(int x, int total){
double result=(x*1.0)/(total*1.0);
System.out.println(result);
DecimalFormat df1=new DecimalFormat("0.0000%");
- 百合——————>怎么学习计算机语言
百合不是茶
java 移动开发
对于一个从没有接触过计算机语言的人来说,一上来就学面向对象,就算是心里上面接受的了,灵魂我觉得也应该是跟不上的,学不好是很正常的现象,计算机语言老师讲的再多,你在课堂上面跟着老师听的再多,我觉得你应该还是学不会的,最主要的原因是你根本没有想过该怎么来学习计算机编程语言,记得大一的时候金山网络公司在湖大招聘我们学校一个才来大学几天的被金山网络录取,一个刚到大学的就能够去和
- linux下tomcat开机自启动
bijian1013
tomcat
方法一:
修改Tomcat/bin/startup.sh 为:
export JAVA_HOME=/home/java1.6.0_27
export CLASSPATH=$CLASSPATH:$JAVA_HOME/lib/tools.jar:$JAVA_HOME/lib/dt.jar:.
export PATH=$JAVA_HOME/bin:$PATH
export CATALINA_H
- spring aop实例
bijian1013
javaspringAOP
1.AdviceMethods.java
package com.bijian.study.spring.aop.schema;
public class AdviceMethods {
public void preGreeting() {
System.out.println("--how are you!--");
}
}
2.beans.x
- [Gson八]GsonBuilder序列化和反序列化选项enableComplexMapKeySerialization
bit1129
serialization
enableComplexMapKeySerialization配置项的含义
Gson在序列化Map时,默认情况下,是调用Key的toString方法得到它的JSON字符串的Key,对于简单类型和字符串类型,这没有问题,但是对于复杂数据对象,如果对象没有覆写toString方法,那么默认的toString方法将得到这个对象的Hash地址。
GsonBuilder用于
- 【Spark九十一】Spark Streaming整合Kafka一些值得关注的问题
bit1129
Stream
包括Spark Streaming在内的实时计算数据可靠性指的是三种级别:
1. At most once,数据最多只能接受一次,有可能接收不到
2. At least once, 数据至少接受一次,有可能重复接收
3. Exactly once 数据保证被处理并且只被处理一次,
具体的多读几遍http://spark.apache.org/docs/lates
- shell脚本批量检测端口是否被占用脚本
ronin47
#!/bin/bash
cat ports |while read line
do#nc -z -w 10 $line
nc -z -w 2 $line 58422>/dev/null2>&1if[ $?-eq 0]then
echo $line:ok
else
echo $line:fail
fi
done
这里的ports 既可以是文件
- java-2.设计包含min函数的栈
bylijinnan
java
具体思路参见:http://zhedahht.blog.163.com/blog/static/25411174200712895228171/
import java.util.ArrayList;
import java.util.List;
public class MinStack {
//maybe we can use origin array rathe
- Netty源码学习-ChannelHandler
bylijinnan
javanetty
一般来说,“有状态”的ChannelHandler不应该是“共享”的,“无状态”的ChannelHandler则可“共享”
例如ObjectEncoder是“共享”的, 但 ObjectDecoder 不是
因为每一次调用decode方法时,可能数据未接收完全(incomplete),
它与上一次decode时接收到的数据“累计”起来才有可能是完整的数据,是“有状态”的
p
- java生成随机数
cngolon
java
方法一:
/**
* 生成随机数
* @author
[email protected]
* @return
*/
public synchronized static String getChargeSequenceNum(String pre){
StringBuffer sequenceNum = new StringBuffer();
Date dateTime = new D
- POI读写海量数据
ctrain
海量数据
import java.io.FileOutputStream;
import java.io.OutputStream;
import org.apache.poi.xssf.streaming.SXSSFRow;
import org.apache.poi.xssf.streaming.SXSSFSheet;
import org.apache.poi.xssf.streaming
- mysql 日期格式化date_format详细使用
daizj
mysqldate_format日期格式转换日期格式化
日期转换函数的详细使用说明
DATE_FORMAT(date,format) Formats the date value according to the format string. The following specifiers may be used in the format string. The&n
- 一个程序员分享8年的开发经验
dcj3sjt126com
程序员
在中国有很多人都认为IT行为是吃青春饭的,如果过了30岁就很难有机会再发展下去!其实现实并不是这样子的,在下从事.NET及JAVA方面的开发的也有8年的时间了,在这里在下想凭借自己的亲身经历,与大家一起探讨一下。
明确入行的目的
很多人干IT这一行都冲着“收入高”这一点的,因为只要学会一点HTML, DIV+CSS,要做一个页面开发人员并不是一件难事,而且做一个页面开发人员更容
- android欢迎界面淡入淡出效果
dcj3sjt126com
android
很多Android应用一开始都会有一个欢迎界面,淡入淡出效果也是用得非常多的,下面来实现一下。
主要代码如下:
package com.myaibang.activity;
import android.app.Activity;import android.content.Intent;import android.os.Bundle;import android.os.CountDown
- linux 复习笔记之常见压缩命令
eksliang
tar解压linux系统常见压缩命令linux压缩命令tar压缩
转载请出自出处:http://eksliang.iteye.com/blog/2109693
linux中常见压缩文件的拓展名
*.gz gzip程序压缩的文件
*.bz2 bzip程序压缩的文件
*.tar tar程序打包的数据,没有经过压缩
*.tar.gz tar程序打包后,并经过gzip程序压缩
*.tar.bz2 tar程序打包后,并经过bzip程序压缩
*.zi
- Android 应用程序发送shell命令
gqdy365
android
项目中需要直接在APP中通过发送shell指令来控制lcd灯,其实按理说应该是方案公司在调好lcd灯驱动之后直接通过service送接口上来给APP,APP调用就可以控制了,这是正规流程,但我们项目的方案商用的mtk方案,方案公司又没人会改,只调好了驱动,让应用程序自己实现灯的控制,这不蛋疼嘛!!!!
发就发吧!
一、关于shell指令:
我们知道,shell指令是Linux里面带的
- java 无损读取文本文件
hw1287789687
读取文件无损读取读取文本文件charset
java 如何无损读取文本文件呢?
以下是有损的
@Deprecated
public static String getFullContent(File file, String charset) {
BufferedReader reader = null;
if (!file.exists()) {
System.out.println("getFull
- Firebase 相关文章索引
justjavac
firebase
Awesome Firebase
最近谷歌收购Firebase的新闻又将Firebase拉入了人们的视野,于是我做了这个 github 项目。
Firebase 是一个数据同步的云服务,不同于 Dropbox 的「文件」,Firebase 同步的是「数据」,服务对象是网站开发者,帮助他们开发具有「实时」(Real-Time)特性的应用。
开发者只需引用一个 API 库文件就可以使用标准 RE
- C++学习重点
lx.asymmetric
C++笔记
1.c++面向对象的三个特性:封装性,继承性以及多态性。
2.标识符的命名规则:由字母和下划线开头,同时由字母、数字或下划线组成;不能与系统关键字重名。
3.c++语言常量包括整型常量、浮点型常量、布尔常量、字符型常量和字符串性常量。
4.运算符按其功能开以分为六类:算术运算符、位运算符、关系运算符、逻辑运算符、赋值运算符和条件运算符。
&n
- java bean和xml相互转换
q821424508
javabeanxmlxml和bean转换java bean和xml转换
这几天在做微信公众号
做的过程中想找个java bean转xml的工具,找了几个用着不知道是配置不好还是怎么回事,都会有一些问题,
然后脑子一热谢了一个javabean和xml的转换的工具里,自己用着还行,虽然有一些约束吧 ,
还是贴出来记录一下
顺便你提一下下,这个转换工具支持属性为集合、数组和非基本属性的对象。
packag
- C 语言初级 位运算
1140566087
位运算c
第十章 位运算 1、位运算对象只能是整形或字符型数据,在VC6.0中int型数据占4个字节 2、位运算符: 运算符 作用 ~ 按位求反 << 左移 >> 右移 & 按位与 ^ 按位异或 | 按位或 他们的优先级从高到低; 3、位运算符的运算功能: a、按位取反: ~01001101 = 101
- 14点睛Spring4.1-脚本编程
wiselyman
spring4
14.1 Scripting脚本编程
脚本语言和java这类静态的语言的主要区别是:脚本语言无需编译,源码直接可运行;
如果我们经常需要修改的某些代码,每一次我们至少要进行编译,打包,重新部署的操作,步骤相当麻烦;
如果我们的应用不允许重启,这在现实的情况中也是很常见的;
在spring中使用脚本编程给上述的应用场景提供了解决方案,即动态加载bean;
spring支持脚本