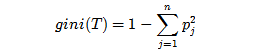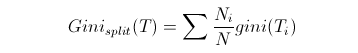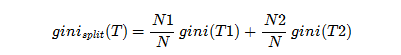机器学习经典算法详解及Python实现--CART分类决策树、回归树和模型树

摘要：

Classification And Regression Tree(CART)是一种很重要的机器学习算法，既可以用于创建分类树（Classification Tree），也可以用于创建回归树（Regression Tree），本文介绍了CART用于离散标签分类决策和连续特征回归时的原理。决策树创建过程分析了信息混乱度度量Gini指数、连续和离散特征的特殊处理、连续和离散特征共存时函数的特殊处理和后剪枝；用于回归时则介绍了回归树和模型树的原理、适用场景和创建过程。个人认为，回归树和模型树可以被看做“群落分类”算法，群落内标签值连续分布，群落间有分界。

（一）认识CART算法

Classification And Regression Tree(CART)是决策树的一种，并且是非常重要的决策树，属于Top Ten Machine Learning Algorithm。顾名思义，CART算法既可以用于创建分类树（Classification Tree），也可以用于创建回归树（Regression Tree）、模型树（Model Tree），两者在建树的过程稍有差异。前文“机器学习经典算法详解及Python实现--决策树（Decision Tree）”详细介绍了分类决策树原理以及ID3、C4.5算法，本文在该文的基础上详述CART算法在决策树分类以及树回归中的应用。

创建分类树递归过程中，CART每次都选择当前数据集中具有最小Gini信息增益的特征作为结点划分决策树。ID3算法和C4.5算法虽然在对训练样本集的学习中可以尽可能多地挖掘信息，但其生成的决策树分支、规模较大，CART算法的二分法可以简化决策树的规模，提高生成决策树的效率。对于连续特征，CART也是采取和C4.5同样的方法处理。为了避免过拟合(Overfitting)，CART决策树需要剪枝。预测过程当然也就十分简单，根据产生的决策树模型，延伸匹配特征值到最后的叶子节点即得到预测的类别。

创建回归树时，观察值取值是连续的、没有分类标签，只有根据观察数据得出的值来创建一个预测的规则。在这种情况下，Classification Tree的最优划分规则就无能为力，CART则使用最小剩余方差(Squared Residuals Minimization)来决定Regression Tree的最优划分，该划分准则是期望划分之后的子树误差方差最小。创建模型树，每个叶子节点则是一个机器学习模型，如线性回归模型。

CART算法的重要基础包含以下三个方面：

（1）二分(Binary Split)：在每次判断过程中，都是对观察变量进行二分。

CART算法采用一种二分递归分割的技术，算法总是将当前样本集分割为两个子样本集，使得生成的决策树的每个非叶结点都只有两个分枝。因此CART算法生成的决策树是结构简洁的二叉树。因此CART算法适用于样本特征的取值为是或非的场景，对于连续特征的处理则与C4.5算法相似。

（2）单变量分割(Split Based on One Variable)：每次最优划分都是针对单个变量。

（3）剪枝策略：CART算法的关键点，也是整个Tree-Based算法的关键步骤。

剪枝过程特别重要，所以在最优决策树生成过程中占有重要地位。有研究表明，剪枝过程的重要性要比树生成过程更为重要，对于不同的划分标准生成的最大树(Maximum Tree)，在剪枝之后都能够保留最重要的属性划分，差别不大。反而是剪枝方法对于最优树的生成更为关键。

（二）CART分类决策树

1，CART的信息论基础和算法过程

CART与C4.5的不同之处是节点分裂建立在GINI指数这个概念上，GINI指数主要是度量数据划分或训练数据集D的不纯度为主。GINI值越小，表明样本的纯净度越高（即该样本只属于同一类的概率越高）。衡量出数据集某个特征所有取值的Gini指数后，就可以得到该特征的Gini Split info，也就是GiniGain。不考虑剪枝情况下，分类决策树递归创建过程中就是每次选择GiniGain最小的节点做分叉点，直至子数据集都属于同一类或者所有特征用光了。

因为CART二分的特性，当训练数据具有两个以上的类别，CART需考虑将目标类别合并成两个超类别，这个过程称为双化。超类别总如何进一步区分类别呢？根据别的特征进一步分类？TBD

（1）Gini指数的概念：

GINI指数是一种不等性度量，通常用来度量收入不平衡，可以用来度量任何不均匀分布，是介于0~1之间的数，0-完全相等，1-完全不相等。分类度量时，总体内包含的类别越杂乱，GINI指数就越大(跟熵的概念很相似)。

对于一个数据集T，其Gini计算方式为：

 （n表示类别数，pj表数据集样本不同类别的概率）

（2）GiniGain

衡量出某个特征所有取值的Gini指数就可以得到Gini Split Info

，i表示特征的第i个取值

ID3算法中的信息增益相似，这个可以称为是Gini信息增益--Gini Gain。对于CART，i=（1,2），得到在Binary Split情况下的Gini信息增益：

2，对离散分布、且取值数目>=3的特征的处理：

正是因为CART树是二叉树，所以对于样本的有N>=3个取值的离散特征的处理时也只能有两个分支，这就要通过组合人为的创建二取值序列并取GiniGain最小者作为树分叉决策点。如某特征值具有['young','middle','old']三个取值,那么二分序列会有如下3种可能性(空集和满集在CART分类中没有意义):

[(('young',), ('middle', 'old')), (('middle',), ('young', 'old')), (('old',), ('young', 'middle'))]

采用CART算法，就需要分别计算按照上述List中的二分序列做分叉时的Gini指数，然后选取产生最小的GINIGain的二分序列做该特征的分叉二值序列参与树构建的递归。如果某特征取值有4个，那么二分序列组合就有7种，5个取值就有15种组合，创建多值离散特征二分序列组合可采用Python的itertools包，程序如下：

from itertools import *
import pdb
def featuresplit(features):
    count = len(features)
    featureind = range(count)
    featureind.pop(0) #get value 1~(count-1)
    combiList = []
    for i in featureind:
        com = list(combinations(features, len(features[0:i])))
        combiList.extend(com)
    combiLen = len(combiList)
    featuresplitGroup = zip(combiList[0:combiLen/2], combiList[combiLen-1:combiLen/2-1:-1])
    return featuresplitGroup
if __name__ == '__main__':
    test= range(3)
    splitGroup = featuresplit(test)
    print 'splitGroup', len(splitGroup), splitGroup
    test= range(4)
    splitGroup = featuresplit(test)
    print 'splitGroup', len(splitGroup),splitGroup
    test= range(5)
    splitGroup = featuresplit(test)
    print 'splitGroup', len(splitGroup),splitGroup
    test= ['young','middle','old']
    splitGroup = featuresplit(test)
    print 'splitGroup', len(splitGroup),splitGroup

因此CART不适用于离散特征有多个取值可能的场景。此时，若定要使用CART，则最好预先人为的将离散特征的取值缩减。

那么对于二分后的左右分支，如果特征取值tuple中元素多于2个，该特征是否还要继续参与当前子数据集的二分呢？TBD

我认为需要，因此该特征继续参与分类决策树递归，直至左右分支上该特征的取值都是唯一的（即不再包含该特征）。那么离散特征的datasplit函数就应该：如果按照当前分支特征分叉后，分支上特征取值tuple>=2，则分支子数据集保留该特征，该tuple继续参与上的树构建的递归；否则分支子数据集删除该特征。

def splitDataSet(dataSet, axis, valueTuple):
    '''return dataset satisfy condition dataSet[i][axis] == valueTuple,
    and remove dataSet[i][axis] if len(valueTuple)==1'''
    retDataSet = []
    length = len(valueTuple)
    if length ==1:
      for featVec in dataSet:
        if featVec[axis] == valueTuple[0]:
            reducedFeatVec = featVec[:axis]     #chop out axis used for splitting
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    else:
      for featVec in dataSet:
        if featVec[axis] in valueTuple:
            retDataSet.append(featVec)
    return retDataSet

3，对连续特征的处理

连续属性参考C4.5的离散化过程，区别在于CART算法中要以GiniGain最小作为分界点选取标准。是否需要修正？处理过程为：

先把连续属性转换为离散属性再进行处理。虽然本质上属性的取值是连续的，但对于有限的采样数据它是离散的，如果有N条样本，那么我们有N-1种离散化的方法：<=v_j的分到左子树，>v_j的分到右子树。计算这N-1种情况下最大的信息增益率。另外，对于连续属性先进行排序（升序），只有在决策属性（即分类发生了变化）发生改变的地方才需要切开，这可以显著减少运算量。

（1） 对特征的取值进行升序排序

（2） 两个特征取值之间的中点作为可能的分裂点，将数据集分成两部分，计算每个可能的分裂点的GiniGain。优化算法就是只计算分类属性发生改变的那些特征取值

（3）选择GiniGain最小的分裂点作为该特征的最佳分裂点（注意，若修正则此处需对最佳分裂点的Gini Gain减去log2(N-1)/|D|（N是连续特征的取值个数，D是训练数据数目）

实现连续特征数据集划分的Python程序为(采用Numpy matrix，连续特征取值就可以省略排序这一步了)：

Source Code:▼Copy

def binSplitDataSet(dataSet, feature, value):
    mat0 = dataSet[nonzero(dataSet[:,feature] > value)[0],:][0]
    mat1 = dataSet[nonzero(dataSet[:,feature] <= value)[0],:][0]
    return mat0,mat1

其中dataset为numpy matrix， feature为dataset连续特征在dataset所有特征中的index，value即为feature的一个取值。

必须注意的是：根据离散特征分支划分数据集时，子数据集中不再包含该特征（因为每个分支下的子数据集该特征的取值就会是一样的，信息增益或者Gini Gain将不再变化）；而根据连续特征分支时，各分支下的子数据集必须依旧包含该特征（当然，左右分支各包含的分别是取值小于、大于等于分裂值的子数据集），因为该连续特征再接下来的树分支过程中可能依旧起着决定性作用。

4，训练数据汇总离散特征和连续特征混合存在时的处理

C4.5和CART算法决策树创建过程中，由于离散特征和连续特征的处理函数不同。当训练数据中两种特征并存时必须能够识别分布类型，从而调用相应的函数。那么有两种方法：

（1）每个特征注明是连续分布还是离散分布，如0表示离散、1表示连续.如此训练、决策时都可以分辨分布类型。

（2）函数中根据特征取值的个数判定，如featureValueCount>10（当然，离散特征取值不可能这么多）则为连续分布，否则为离散分布。此时构建的决策树模型中，必须注明特征的分布类型（如构建一个List，长度为featureCount，其中元素0：离散，1：连续）。

Note:对于取值为是或者否的离散特征，将其按离散或者连续分布处理均可。按照连续分布反而简单，取std=0.5即可简单的实现split。此时分布判断标准更改为featureValueCount>20 or ==2。

(3) 利用独热编码（OneHotEncoding），Python sklearn 的preprocessing提供了OneHotEncoder()能够将离散值转换成连续值处理。独热编码即 One-Hot 编码，又称一位有效编码，其方法是使用N位状态寄存器来对N个状态进行编码，每个状态都由他独立的寄存器位，并且在任意时候，其中只有一位有效。对于每一个特征，如果它有m个可能值，那么经过独热编码后，就变成了m个二元特征。并且，这些特征互斥，每次只有一个激活。因此，数据会变成稀疏的。这样做的好处主要有：解决了分类器不好处理属性数据的问题、在一定程度上也起到了扩充特征的作用。参考‘OneHotEncoder进行数据预处理’。

5，CART的剪枝

分析分类回归树的递归建树过程，不难发现它实质上存在着一个数据过度拟合问题。在决策树构造时，由于训练数据中的噪音或孤立点，许多分枝反映的是训练数据中的异常，使用这样的判定树对类别未知的数据进行分类，分类的准确性不高。因此试图检测和减去这样的分支，检测和减去这些分支的过程被称为树剪枝。树剪枝方法用于处理过分适应数据问题。通常，这种方法使用统计度量，减去最不可靠的分支，这将导致较快的分类，提高树独立于训练数据正确分类的能力。决策树常用的剪枝常用的简直方法有两种：预剪枝(Pre-Pruning)和后剪枝(Post-Pruning)。预剪枝是根据一些原则及早的停止树增长，如树的深度达到用户所要的深度、节点中样本个数少于用户指定个数、不纯度指标下降的最大幅度小于用户指定的幅度等；后剪枝则是通过在完全生长的树上剪去分枝实现的，通过删除节点的分支来剪去树节点，可以使用的后剪枝方法有多种，比如：代价复杂性剪枝、最小误差剪枝、悲观误差剪枝等等。

CART常采用事后剪枝方法，构建决策树过程中的第二个关键就是用独立的验证数据集对训练集生长的树进行剪枝。TBD

关于后剪枝的具体理论可以参考“数据挖掘十大经典算法--CART: 分类与回归树”剪枝部分。

6，Python实现CART决策树

相对于ID3、C4.5决策树算法，CART算法的的实现过程在结构上是类似的，区别在于：

（1）最佳特征度量采取Gini Gain，因此calcShannonEnt方法要替换成calcGini方法

（2）CART采取二分法，因此对于有多个取值的离散特征，需要首先获取最小二分序列及其GiniGain，因此splitDataSet方法需按照取值tuple分开、chooseBestFetureToSplit要返回最佳分叉点及其二分序列如(('middle',), ('young', 'old'))。

（3）决策树模型判决算法中对于离散特征也要根据特征值Tuple进行，即判断特征值取值属于左分支还是有分支；对于连续特征则是判断特征值取值是大于分裂值还是小于等于分裂值。

（三）CART回归树和模型树

当数据拥有众多特征并且特征之间关系十分复杂时，构建全局模型的想法就显得太难了，也略显笨拙。而且，实际生活中很多问题都是非线性的，不可能使用全局线性模型来拟合任何数据。一种可行的方法是将数据集切分成很多份易建模的数据，然后利用线性回归技术来建模。如果首次切分后仍然难以拟合线性模型就继续切分。在这种切分方式下，树结构和回归法就相当有用。

回归树与分类树的思路类似，但叶节点的数据类型不是离散型，而是连续型，对CART稍作修改就可以处理回归问题。CART算法用于回归时根据叶子是具体指还是另外的机器学习模型又可以分为回归树和模型树。但无论是回归树还是模型树，其适用场景都是：标签值是连续分布的，但又是可以划分群落的，群落之间是有比较鲜明的区别的，即每个群落内部是相似的连续分布，群落之间分布确是不同的。所以回归树和模型树既算回归，也称得上分类。

回归是为了处理预测值是连续分布的情景，其返回值应该是一个具体预测值。回归树的叶子是一个个具体的值，从预测值连续这个意义上严格来说，回归树不能称之为“回归算法”。因为回归树返回的是“一团”数据的均值，而不是具体的、连续的预测值（即训练数据的标签值虽然是连续的，但回归树的预测值却只能是离散的）。所以回归树其实也可以算为“分类”算法，其适用场景要具备“物以类聚”的特点，即特征值的组合会使标签属于某一个“群落”，群落之间会有相对鲜明的“鸿沟”。如人的风格是一个连续分布，但是却又能“群分”成文艺、普通和2B三个群落，利用回归树可以判断一个人是文艺还是2B，但却不能度量其有多文艺或者多2B。所以，利用回归树可以将复杂的训练数据划分成一个个相对简单的群落，群落上可以再利用别的机器学习模型再学习。

模型树的叶子是一个个机器学习模型，如线性回归模型，所以更称的上是“回归”算法。利用模型树就可以度量一个人的文艺值了。

回归树和模型树也需要剪枝,剪枝理论和分类树相同。为了获得最佳模型，树剪枝常采用预剪枝和后剪枝结合的方法进行。

那么如何利用CART构建回归树或者模型树呢？且听下面细细道来。

1，回归树-利用差值选择分支特征

树回归中，为成功构建以分段常数为叶节点的树，需要度量出数据的一致性。分类决策树创建时会在给定节点时计算分类数据的混乱度。那么如何计算连续型数值的混乱度呢？ 事实上， 在连续数据集上计算混乱度是非常简单的--度量按某一特征划分前后标签数据总差值，每次选取使数据总差值最小的那个特征做最佳分支特征为了对正负差值同等看待，一般使用绝对值或平方值来代替上述差值）。为什么选择计算差值呢》差值越小，相似度越高，越可能属于一个群落咯。那么如果选取方差做差值，总方差的计算方法有两种：

（1）计算数据集均值std，计算每个数据点与std的方差，然后n个点求和。

（2）计算数据集方差var，然后var_sum = var*n，n为数据集数据数目。Python Matrix中可以利用var方法求得数据集方差，因此该方法简单、方便。

与Gini Gain对离散特征和连续特征的处理方法类似，多值离散特征需要选择最优二分序列，连续特征则要找出最优分裂点。

那么，每次最佳分支特征的选取过程为：

function chooseBestSplitFeature()

(1)先令最佳方差为无限大bestVar=inf。

(2)依次计算根据某特征（FeatureCount次迭代）划分数据后的总方差currentVar（，计算方法为：划分后左右子数据集的总方差之和），如果currentVar

(3)返回最佳分支特征、分支特征值（离散特征则为二分序列、连续特征则为分裂点的值），左右分支子数据集。

2，采取线性回归预测偏差构建模型树

用树来对数据建模，除了把叶节点简单地设定为常数值之外，还有一种方法是把叶节点设定为分段线性函数，这里所谓的分段线性（piecewise linear)是指模型由多个线性片段组成，这就是模型树。模型树的可解释性是它优于回归树的特点之一。另外，模型树也具有更髙的预测准确度。

模型树的创建过程大体上与回归树是一样的，区别就在于递归过程中最佳分支特征选取时差值的计算。对于模型树：给定的数据集先用线性的模型来对它进行拟合，然后计算真实的目标值与模型预测值间的差值，将这些差值的平方求和就得到了所需的总差值，最后依然选取总差值最小的特征做分支特征。至于线性回归采用哪种解法，就要参看线性回归模型的求解了。

3，CART回归树和模型树的Python实现

CART回归树和模型树学习包的下载地址是：

TBD

引用：

DecisionTree：CART、剪枝

本文作者Adan，来源于:机器学习经典算法详解及Python实现--CART分类决策树分类和回归树。转载请注明出处。