CNN的发展

卷及神经网络（Convolutional Neural Networks, CNN）的发展

CNN的基本组成

卷积神经网络是一类包含卷积计算，且具有深度结构的前馈神经网络，卷积神经网络具有表征学习的能力，能够按其阶层结构对输入信息进行平移不变分类，也被称为平移不变人工神经网络

卷积神经网络仿造生物视觉机制构建，可以进行监督学习和非监督学习，其隐含层内的卷积核参数共享和层间连接的稀疏性使得卷积神经网络能够以较小的计算量对格点化特征

​ -----------------------------以上摘自百度百科《卷积神经网络》

一般CNN含有三种类型的神经网络层：

• 卷积层（Convolutions layers）：学习输入数据的特征表示，卷积层有很多的卷积核（convolutional kernel）组成，卷积核用来计算不同的特征图（feature map），激活函数（activation function）给CNN卷积神经网络引入了非线性，常用的有sigmoid，tanh，relu

• 池化层（Pooling layers）：降低卷积层输入的特征向量，同时改善效果，使结构不容易出现过拟合，典型的操作有平均池化和最大池化。通过卷积层和池化层，可以获得更多的抽象特征

• 全连接层（Full connected layers）：将卷积层和池化层堆叠起来以后，能够形成一层或者多层全连接层，这样就能够实现高阶的推理能力，在整个卷积神经网络中起到“分类器”的作用。

  如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用，所以，sigmoid/tanh常见于全连接层，relu则常用语卷积层

1.LeNet-5模型（Yann LeCun）

结构

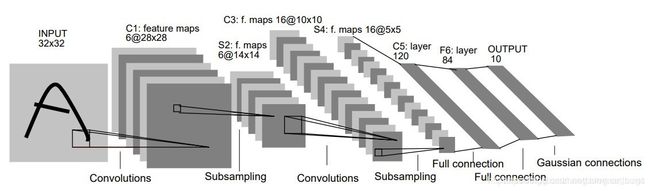
LeNet-5模型共有7层

• 第一层：卷积层

  input=(32,32,1)，本层包含6个大小为（5,5）步长为1的卷积核，padding=valid，output=（28,28,6）

• 第二层：池化层

  对上一层的输出做2x2的最大池化，output=（14,14,6）

• 第三层：卷积层

  input=（14,14,6），本层有16个大小为（5,5），步长为1的卷积核，padding=valid，output=（10,10,16）

• 第四层：池化层

  做2x2的最大池化，output=（5,5,16）

• 第五层：全连接层

  将上层的所有神经元展开作为输入，共包含120个神经元

• 第六层：全连接层

  包含84个神经元

• 第七层：全连接层

  包含10个神经元，分别代表数字0-9

• 第八层：激活函数

  前七层使用的是tanh激活，最后一层使用softmax激活

代码实现

# LeNet-5模型的定义
model = Sequential()
model.add(Conv2D(filters = 6,
                 kernel_size = (5,5),
                 padding = "valid",
                 input_shape = (28,28,1),
                 activation = "tanh"))
model.add(MaxPool2D(pool_size = (2,2)))
model.add(Conv2D(filters = 16,
                 kernel_size = (5,5),
                 padding = "valid",
                 activation = "tanh"))
model.add(MaxPool2D(pool_size = (2,2)))
model.add(Flatten())
model.add(Dense(120,activation = "tanh"))
model.add(Dense(84,activation = "tanh"))
model.add(Dense(10,activation = "softmax"))

2.AlexNet模型（Hinton）

结构

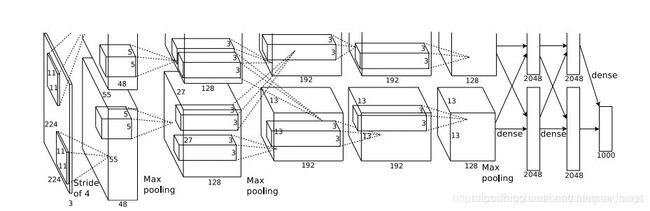
从上面可以看出，模型分为上、下两个部分的网络，这两个部分的网络是分别用两个GPU训练的，只有到了特定的网络层后才需要两块GPU交互，这种设置完全是利用两个GPU来提高运算效率，在网络结构上差异不大，所以可以当成一块GPU来看待

那么AlexNet的整个网络结构就是由5个卷积层和3个全连接层组成，总共8层

• 卷积层C1

  卷积：input=（227，227，3），filters=96，kernel_size=（11,11），strides=（4,4），padding=valid，output=（55,55,96）

  激活：ReLU，将卷积层得到的feature map输入激活函数

  池化：poo_size=（3,3），strides=（2,2）（重叠池化，步长小于池化单元的宽度）output=（27,27,96） 27=（55-3）/2+1

  局部响应归一化：使用k=2，n=5，α=10-4，β=0.75进行局部归一化，输出仍为（27,27,96）

  输出分为两组，每组大小为（27,27,48）

• 卷积层C2

  卷积：input=（27,27，48），filters=128，kernel_size=（5,5），padding=2，strides=1，output=（27,27,128）

  激活：ReLU，将卷积得到的feature map输入

  池化：poo_size=（3,3），strides=（2,2），output=（13,13,256），p.s（这里是256是因为分别用两块GPU训练，每个的通道数是128，所以合起来是256）

  局部响应归一化：使用k=2，n=5，α=10-4，β=0.75进行局部归一化，输出仍为（13,13,256）

  输出分为两组，每组大小为（13,13,128）

• 卷积层C3

  卷积：input=(13,13,128)，filters=192，kernel_size=（3,3），padding=same，

  strides=(1,1)，output=（13,13,192），p.s，有的地方会将卷积核个数写成192*2=384，这是因为有两块GPU

  激活：ReLU，将卷积层输出的FeatureMap输入到ReLU函数中

• 卷积层C4（和卷积层C3类似）

  卷积：input=（13,13,192），filters=192，kernel_size=（3,3），padding=same，strides=（1,1），output=（13,13,192）

  激活：ReLU，将卷积层输出的FeatureMap输入到ReLU函数中

• 卷积层C5

  卷积：input=（13,13,192），filters=128，kernel_size=（3,3），padding=same，strides=（1,1），output=（13,13,128）

  激活：ReLU，将卷积层输出的FeatureMap输入到ReLU函数中

  池化：poo_size=（3,3），strides=（2,2），output=（6,6,128）

• 全连接层FC6

  卷积 --> 全连接：input=（13,13,128），filters=2048

  激活：这2048个运算结果通过ReLU激活函数生成2048个值

  Dropout：抑制过拟合，随机断开某些神经元的连接，或者不激活某些神经元

• 全连接层FC7

  全连接：input=（2048，），output=（2048，）

  激活：这2048个运算结果通过ReLU激活函数生成2048个值

  Dropout：抑制过拟合，随机断开某些神经元的连接，或者不激活某些神经元

• 全连接层FC8

  input=（4096，），output=（1000，）

  激活：softmax激活，一共1000个分类

模型特点

• 1.激活函数的改变

  原来的网络激活函数多是sigmoid/tanh，这两个函数最大的缺点就是其饱和性（当输入的x过大或过小时，斜率非常小，在使用梯度下降时容易造成梯度消失）

  ReLU函数的表示为max(0,x)，也就是说，当x>0时，输出为x，斜率恒为1，实际使用时，神经网络的收敛速度要比传统激活函数快10倍

• 2.多GPU分布式计算

• 3.局部响应归一化（Local Response Normalization）

  这个技术被后来证明是没作用的…

• 4.覆盖的池化操作（Overlapping Pooling）

  池化主要起到提取主要特征，减少特征图尺寸的作用

  一般的池化是没有重叠的，也就是说，pool_size=strides，当pool_size>strides时，就成了overlapping pooling，这种操作类似于convolutional的操作，可以得到更准确的结果，并且该操作更不容易过拟合

• 5.减少过拟合

  • Data augmentation（数据增强）

  • Dropout

    Dropout是神经网络中一种非常有效的减少过拟合的方法，对每个神经元设置一个一个keep_prob用来表示这个神经元被保留的概率，如果神经元没被保留，换句话说这个神经元被"dropout"了，那么这个神经元的输出被设置为0，在残差反向传播时，传播到该神经元的值也为0，因此可以认为神经网络中不存在这个神经元；而在下次迭代中，所有神经元将会根据keep_prob被重新随机dropout。相当于每次迭代，神经网络的拓扑结构都会有所不同，这就会迫使神经网络不会过度依赖某几个神经元或者说某些特征。因此，神经元会被迫去学习更具有鲁棒性的特征。

代码实现

# 定义AlexNet模型
model = Sequential()
# 1block
model.add(Conv2D(filters = 97,
                 kernel_size = (11,11),
                 strides = (4,4),
                 padding = "valid",
                 input_shape = (224,224,3)))
model.add(Activation("relu"))
model.add(MaxPool2D(pool_size = (2,2),
                    strides = (2,2),
                    padding = "valid"))
model.add(BatchNormalization())
# 2block
model.add(Conv2D(filters = 256,
                 kernel_size = (11,11),
                 strides = (1,1),
                 padding = "valid"))
model.add(Activation("relu"))
model.add(MaxPool2D(pool_size = (2,2),
                    strides = (2,2),
                    padding = "valid"))
model.add(BatchNormalization())
# 3 block
model.add(Conv2D(filters = 384,
                 kernel_size = (3,3),
                 strides = (1,1),
                 padding = "valid"))
model.add(Activation("relu"))
model.add(BatchNormalization())
# 4 block
model.add(Conv2D(filters = 384,
                 kernel_size = (3,3),
                 strides = (1,1),
                 padding = "valid"))
model.add(Activation("relu"))
model.add(BatchNormalization())
# 5 block
model.add(Conv2D(filters = 256,
                 kernel_size = (3,3),
                 strides = (1,1),
                 padding = "valid"))
model.add(Activation("relu"))
model.add(MaxPool2D(pool_size = (2,2),
                    strides = (2,2),
                    padding = "valid"))
model.add(BatchNormalization())
# 6 dense
model.add(Flatten())
model.add(Dense(4096, input_shape=(224*224*3,)))
model.add(Activation("relu"))
model.add(Dropout(0.4))
model.add(BatchNormalization())
# 7 dense
model.add(Dense(4096))
model.add(Activation("relu"))
model.add(Dropout(0.4))
model.add(BatchNormalization())
# 8 dense
model.add(Dense(17))
model.add(Activation("softmax"))

3.VGGNet（牛津&DeepMind）

结构

• VGG16结构图

VGGNet探索了卷积神经网络的深度和其性能之间的关系，通过反复堆叠3x3的小型卷积核和2x2的最大池化层，成功构建了16-19层深的卷积神经网络

网络特点

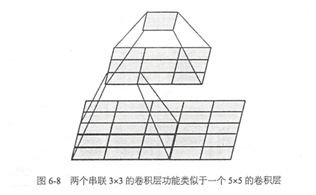
VGGNet全部使用3*3的卷积核和2*2的池化核，通过不断加深网络结构来提升性能。网络层数的增长并不会带来参数量上的爆炸，因为参数量主要集中在最后三个全连接层中。同时，两个3*3卷积层的串联相当于1个5*5的卷积层，3个3*3的卷积层串联相当于1个7*7的卷积层，即3个3*3卷积层的感受野大小相当于1个7*7的卷积层。但是3个3*3的卷积层参数量只有7*7的一半左右，同时前者可以有3个非线性操作，而后者只有1个非线性操作，这样使得前者对于特征的学习能力更强。

使用1*1的卷积层来增加线性变换，输出的通道数量上并没有发生改变。这里提一下1*1卷积层的其他用法，1*1的卷积层常被用来提炼特征，即多通道的特征组合在一起，凝练成较大通道或者较小通道的输出，而每张图片的大小不变。有时1*1的卷积神经网络还可以用来替代全连接层

其他小技巧。VGGNet在训练的时候先训级别A的简单网络，再复用A网络的权重来初始化后面的几个复杂模型，这样收敛速度更快。VGGNet作者总结出LRN层作用不大，越深的网络效果越好，1*1的卷积也是很有效的，但是没有3*3的卷积效果好，因为3*3的网络可以学习到更大的空间特征

代码实现（VGG16）

# 定义VGG16模型
model = Sequential()

# block1
model.add(Conv2D(filters = 64,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block1_conv1",
                 input_shape = (32,32,3)))
model.add(Conv2D(filters = 64,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block1_conv2"))
model.add(MaxPooling2D(pool_size = (2,2),
                       strides = (2,2),
                       name = "block1_pool"))
# block2
model.add(Conv2D(filters = 128,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block2_conv1"))
model.add(Conv2D(filters = 128,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block2_conv2"))
model.add(MaxPooling2D(pool_size = (2,2),
                       strides = (2,2),
                       name = "block2_pool"))
# block3
model.add(Conv2D(filters = 256,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block3_conv1"))
model.add(Conv2D(filters = 256,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block3_conv2"))
model.add(Conv2D(filters = 256,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block3_conv3"))
model.add(MaxPooling2D(pool_size = (2,2),
                       strides = (2,2),
                       name = "block3_pool"))
# block4
model.add(Conv2D(filters = 512,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block4_conv1"))
model.add(Conv2D(filters = 512,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block4_conv2"))
model.add(Conv2D(filters = 512,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block4_conv3"))
model.add(MaxPooling2D(pool_size = (2,2),
                       strides = (2,2),
                       name = "block4_pool"))
# block5
model.add(Conv2D(filters = 512,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block5_conv1"))
model.add(Conv2D(filters = 512,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block5_conv2"))
model.add(Conv2D(filters = 512,
                 kernel_size = (3,3),
                 activation = "relu",
                 padding = "same",
                 name = "block5_conv3"))
model.add(MaxPooling2D(pool_size = (2,2),
                       strides = (2,2),
                       name = "block5_pool"))

model.add(Flatten())
model.add(Dense(4096,activation="relu",name="fc1"))
model.add(Dropout(0.5))
model.add(Dense(4096,activation="relu",name="fc2"))
model.add(Dropout(0.5))
model.add(Dense(10,activation="softmax",name="prediction"))

4.GoogLeNet

结构

GoogLeNet和VGG的相同点就是结构更深了

VGG继承了LeNet以及AlexNet的一些架构，而GoogLeNet则做了更大胆的网络结构尝试，虽然深度只有22层，但大小比AlexNet和VGG小很多，GoogLeNet的参数为500万个，AlexNet的参数是GoogLeNet的12倍，VGG的参数是AlexNet的3倍，因此在内存或资源有限时，GoogLeNet是较好的选择，并且，从模型结果来看，GoogLeNet的性能更加优越

一般来说，提升网络性能最直接的办法就是增加网络深度和宽度，也就意味着巨量的参数，但是巨量参数很容易产生过拟合，也会大大增加计算量

GoogLeNet认为解决上述两个缺点的根本方法是将全连接甚至一般的卷积都转化为稀疏连接，有文献表明，对于大规模稀疏的神经网络，可以通过分析激活值的统计特性和对高度相关的输出进行聚类来逐层构建出一个最优网络，这点表明臃肿的稀疏网络可能被不失性能的简化，fire together,wire together（描述突触可塑性的原理， 即突触前神经元向突触后神经元的持续重复的刺激可以导致突触传递效能的增加）

大量的文献表明可以将稀疏矩阵聚类为较为密集的子矩阵来提高计算性能，据此论文提出了名为Inception 的结构来实现此目的

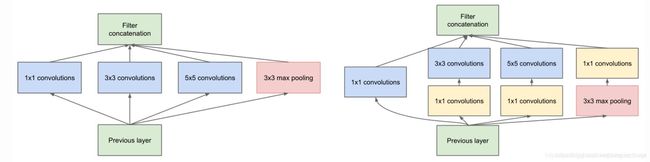
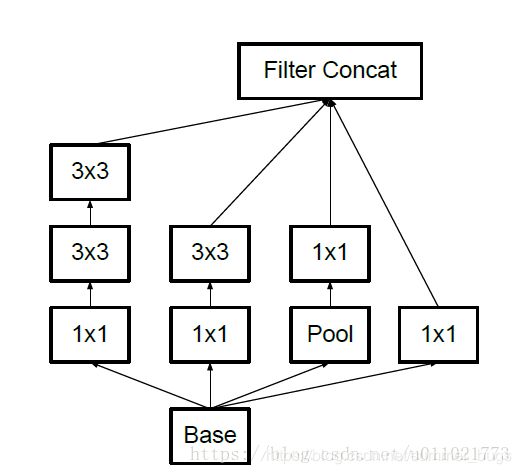
InceptionV1结构

• 说明：

  • 1.采用不同大小的卷积核意味着不同大小的感受野，最后拼接意味着不同尺度特征的融合
  • 2.卷积核选择1,3,5是为了方便对齐，设定卷积步长strides=1之后，只要分别设定padding=0,1,2,那么卷积之后便可以得到相同维度的特征，然后这些特征就可以直接拼接在一起（比方说这一层本来是一个28*28大小的卷积核，一共输出224层，换成inception以后就是64层1*1， 128层3*3， 32层5*5。这样算到最后依然是224层，但是参数个数明显减少了，从28*28*224 = 9834496 变成了1*1*64+3*3*128+5*5*32 = 2089，减小了几个数量级）
  • 3.文章很多地方说明Pooling很有效，所以Inception也加入了
  • 4.网络越到后面，特征越抽象，而且每个特征所涉及的感受野也更大了，因此随着层数的增加，3x3 ，5x5卷积的比例也要增加，但是使用5x5的卷积核仍然会带来巨大的计算量，因此，采用1x1卷积核来进行降维

• 改进后的Inception Module如上右图

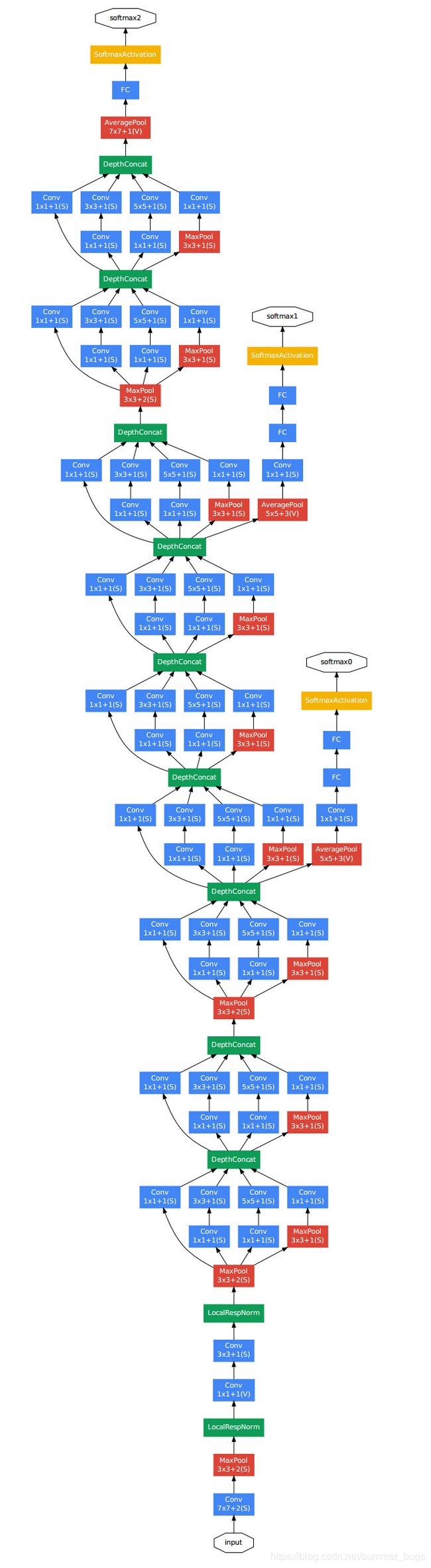
GoogLeNet整体结构图

• 说明：
  • 1.GoogLeNet采用了模块化结构，方便添加和修改
  • 2.网络最后使用AveragePooling来代替全连接层
  • 3.虽然移除了全连接，但是网络中依然使用Dropout
  • 4.为了避免梯度小时，网络额外增加了2个辅助的softmax用于向前传导梯度，但是在实际测试时，这两个额外的softmax会被去掉

关于网络设计的准则

• 1.避免表达瓶颈，特别是在网络靠前的地方。信息流向前传播过程中显然不能经过高度压缩的层（即表达瓶颈），从input到output，feature map的宽和高基本都会逐渐变小，但是不能一下子变得很小（比如上来就kernel_size=7，strides=5），这样显然不合适

  另外，输出的维度channel，一般来说会逐渐增多，否则网络很难训练（特征维度并不代表信息的多少，只是作为一种估计的手段）

• 2.高维特征更易处理。高维度特征更易区分，会加快训练

• 3.可以在低维嵌入上进行空间汇聚（Pooling）而无需担心丢失很多信息，比如在3x3卷积前，可以对输入先进行降维而不会产生严重的后果，假设信息可以被简单压缩，那么训练就会加快

Inception V2

Inception V2学习了VGGNet，用两个3x3卷积核代替5x5的大卷积核（降低参数量的同时减轻了过拟合），同时还提出了BatchNormalization的方法，BN是一个非常有效的正则化方法，可以让大型卷积神经网络的训练速度加快很多杯，同时瘦脸后的分类准确率可以得到大幅提高

BN在用于神经网络某层时，会对每一个mini-batch数据的内部进行标准化处理，使输出规范化到(0,1)的正态分布，减少了Internal Covariate Shift（内部神经元分布的改变）。BN论文指出，传统的深度神经网络在训练时，每一层的输入的分布都在变化，导致训练变得困难，我们只能使用一个很小的学习速率解决这个问题。而对每一层使用BN之后，可以有效解决这个问题，学习速率可以增大很多倍，达到之前的准确率需要迭代的次数需要1/14，训练时间大大缩短

在使用BN时需要注意的地方：

• 增大学习率并加快学习衰减速度以适应BN规范后的数据
• 去除Dropout并减轻L2正则
• 去除LRN
• 更彻底对训练样本进行shuffle
• 减少数据增强过程中对光学的畸变

Inception V3

相对于前面的网络，Inception V3主要在两个方面改造

• 1.引入了Factorization into small convolutions的思想，即将一个较大的二维卷积拆成两个较小的一维卷积（比如将7x7卷积拆成1x7卷积和7x1卷积），一方面节约了大量参数，加速运算并减轻过拟合，同时增加了一层非线性扩展模型的表达能力，（下图是将3x3卷积拆分成1x3和3x1）

• 2.Inception V3优化了Inception Module的结构，现在Inception Module有35x35，17x17，8x8三种不同结构

Inception V4

和V3相比，V4主要结合了ResNet，发现ResNet可以极大加速训练，同时性能也能有所提升

Inception模块代码实现

import keras
from keras.layers import Conv2D,MaxPooling2D,Input

input_img = Input(shape=(256,256,3))

tower_1 = Conv2D(64,(1,1),padding="same",activation="relu")(input_img)
tower_1 = Conv2D(64,(3,3),padding="same",activation="relu")(tower_1)

tower_2 = Conv2D(64,(1,1),padding="same",activation="relu")(input_img)
tower_2 = Conv2D(64,(5,5),padding="same",activation="relu")(tower_2)

tower_3 = MaxPooling2D((3,3),strides=(1,1),padding="same")(input_img)
tower_3 = Conv2D(64,(1,1),padding="same",activation="relu")(tower_3)

output = keras.layers.concatenate([tower_1,tower_2,tower_3],axis=1)

5.ResNet（何凯明等）

当增加网络深度到一定程度的时候，更深的网络意味着更高的训练误差（因为梯度消失的现象越明显，所以在反向传播的时候，无法有效的把梯度更新到前面的网络层，靠前的网络层参数无法更新，导致训练和测试效果变差）

什么是残差

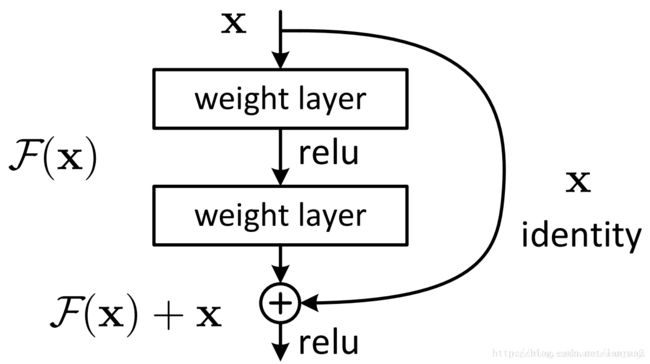
ResNet中提出了两种映射（mapping）：一种是identity mapping，也就是下图中的曲线，另一种是residual mapping，就是除了曲线的那部分，所以，最后的输出应该是$y=F(x)+x$，公式中的x对应的就是identity mapping，而residual mapping指的是”差“，也就是y-x，所以残差就是F(x)的部分

为什么残差结构可以解决问题

从理论上来说，ResNet提供了两种选择方式，也就是identity mapping（恒等映射）和residual mapping（残差映射），如果网络已经达到最优，继续加深网络，residual mapping将会被push为0，只剩下identity mapping，这样理论上网络一直处于最优状态，网络的性能也就不会随着深度的增加而降低

结构

它使用了一种连接方式，叫做”shortcut connection“，也就是”抄近道“

左图被称为building block，右图被称为bottleneck design，就是为了降低参数，通过一个1x1的卷积将256维降低到64维，然后再通过1x1的卷积恢复，整体上用的参数数目：1x1x256x64 + 3x3x64x64 + 1x1x64x256 = 69632，而不使用bottleneck的话就是两个3x3x256的卷积，参数数目: 3x3x256x256x2 = 1179648，差了16.94倍

对于常规的ResNet可以用34层或者更少的网络中，对于Bottleneck Design的ResNet通常用于更深的网络中，目的就是减少计算和参数量

如果F(x)和x的通道数不同该如何？

从上图可以看到，有两种不同的shortcut connection方式

• 实线的connection都是执行的3x3x64的卷积，他们的通道数一致，所以采用的计算方式：

  $y=F(x)+x$

• 虚线的connection分别是3x3x64和3x3x128的卷积操作，他们的channel个数不同，所以采用的计算方式：$y=F(x)+Wx$，其中W是卷积操作，用来调整x的维度的

不同层数的ResNet结构表

6.DenseNet

ResNet模型的核心是通过简历前面层与后界面层之间的”短路连接“，这有助于训练过程中梯度的反向传播，从而训练处更深的CNN网络

DenseNet模型的思路与ResNet一致，但是它建立的是前面所有层与后面层的密集连接（dense connection）

DenseNet的另一大特色是通过特征在channel上的连接来实现特征重用（feature reuse），这些特点让DenseNet在参数和计算成本更少的情况下实现ResNet更优的性能

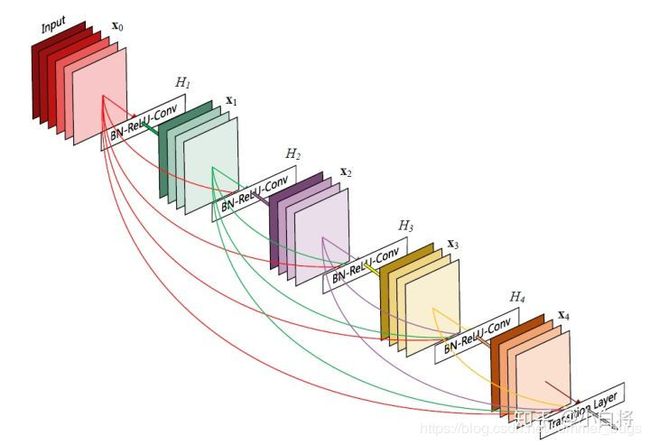
结构

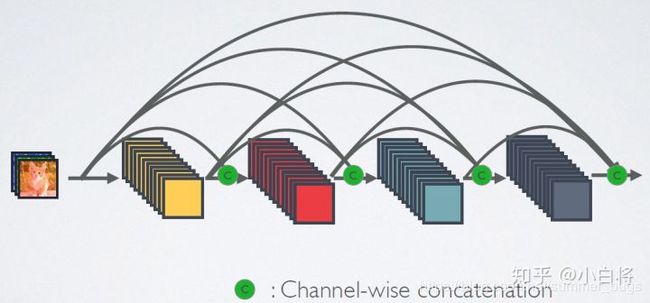
DenseNet的连接机制是：互相连接所有的层，具体来说就是每个层都会接受其前面所有的层作为额外的输入，在DenseNet中，每个层都会与前面所有层在channel维度上进行连接（concatenate）在一起（这里各层的特征图大小是相同的），并作为下一层的输入，对于一个L层网络，DenseNet一共包含$\frac{L(L+1)}{2}$个连接，相比于ResNet，这是一种密集连接，而且，DenseNet是直接concatenate来自不同层的特征图（ResNet是add），这可以实现特征重用，提升效率，这是DenseNet与ResNet的最主要区别

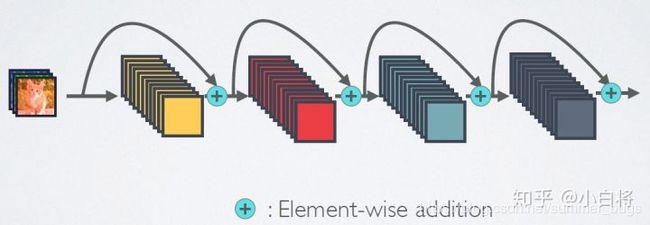
• ResNet的短路连接机制

• DenseNet的密集连接机制

• 公式表示：

  • 传统网络在$l$层的输出：$x_l=H_l(x_{l-1})$
  • 对于ResNet，增加了来自上一层输入的identity函数：$x_l=H_l(x_{l-1})+x_{l-1}$
  • 在DenseNet中，会连接前面所有层作为输入：$x_l=H_l([x_0,x_1,...,x_{l-1}])$

  其中，上面的$H_l(\cdot )$代表非线性转化函数，他是一个组合操作，可能包括一系列的BN，ReLU，Pooling及Conv操作

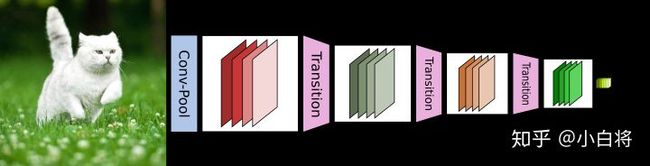
CNN网络一般需要经过Pooling或者stride>1的Conv来降低特征图的大小，而DenseNet的密集连接方式需要特征图大小保持一致，为了解决这个问题，DenseNet网络中使用DenseBlock+Transition的结构，其中DenseBlock是包含很多层的模块，每个层的特征图大小相同，层与层之间采用密集连接方式。而Transition模块是连接两个相邻的DenseBlock，并且通过Pooling使特征图大小降低

DenseNet 具体结构

前面提到DenseNet主要由DenseBlock和Transition组成，具体的网络结构如下

• 在DenseBlock中，各层的特征图大小一致，可以在channel维度上连接。DenseBlock中的非线性组合函数$H(\cdot )$采用的是BN+ReLU+3x3 Conv，如上图所示
• 与ResNet不同，所有DenseBlock中各个层卷机之后均输出k个特征图（也就是说，filters参数相同），即得到特征图的channel为k。k在DenseNet称为growth rate，这是一个超参数。一般情况下，使用较小的k（比如12），就可以得到较好的性能，嘉定输入层的特征图的channel数为$k_0$，那么$l$层输入的的channel数为$k_0+k(l-1)$，因此，随着层数的增加，尽管k设定的较小，DenseBlock的输入会非常多，不过这是由于特征重用造成的，每个层仅有k个特征是自己独有的
• 由于后面层的输入会非常大，DenseBlock内部可以采用bottleneck层来减少计算量，主要是原有的结构中增加1x1 Conv，如下图所示，即BN+ReLU+1x1 Conv+BN+ReLU+3x3 Conv，称为DenseNet-B结构。其中1x1 Conv得到4k个特征图，它起到的作用就是降低特征数量，从而提高计算效率

• 对于Transition层，他主要是连接两个相邻的DenseBlock，并且降低特征图大小

  Transition层包括一个1x1的卷积和2x2的AvgPooling，

  结构为BN+ReLU+1x1 Conv+2x2 AvgPooling。另外，Transition层可以起到压缩模型的作用，假定Transition的上接DenseBlock得到的特征图channels为m，Transition层可以产生$\lfloor \theta m\rfloor$个特征（通过卷积层），其中$\theta \in (0,1]$是压缩系数（compression rate）。当θ=1时，特征个数经过Transition层没有变化，即无压缩，而当压缩系数小于1时，这种结构称为DenseNet-C，论文中使用θ=0.5。对于使用bottleneck层的DenseBlock结构和压缩系数小于1的Transition组合结构称为DenseNet-BC

DenseNet的优势

• 1.由于密集连接的方式，DenseNet提升了梯度的反向传播，使得网络更容易训练，由于每层可以直达最后的误差信号，实现了隐式的“deep supervision”
• 2.参数更小且计算更高效，由于DenseNet是通过concatenate特征来实现短路连接，实现了特征重用，并且采用较小的growth rate，每个层所独有的特征图是比较小的
• 3.由于特征复用，最后的分类器使用了低级特征

7.SENet(Squeeze-and-Excitation Networks)

主体思路

SENet是希望显式的建模特征通道之间的相互依赖关系，并且引入新的空间维度来进行特征通道间的融合，而是采用了一种全新的“特征重标定”策略，具体来说，就是通过学习的方法来自动获取到每个特征通道的重要程度，然后依照这个重要程度去提升有用的特征并去抑制对当前任务用处不大的特征，即引入了channel-wise的attention机制

attention机制的目标：着重更有利于任务的信息，抑制无用/干扰/冗余信息

对于CNN网络来说，其核心计算是卷积算子，通过卷积核从输入特征图学习到新特征图，从本质上讲，卷积是对一个局部区域进行特征融合，这包括空间上（H和W维度）以及通道间（C维度）的特征融合

对于卷积操作，很大一部分工作是提高感受野，即空间上融合更多特征，或者是提取多尺度空间信息，如Inception网络的多分支结构。对于channel维度的特征融合，卷积操作基本上默认对输入特征图的所有channel进行融合，而MobileNet网络中的组卷积（Group Convolution）和深度可分离卷积（Depthwise Separable Convolution）对channel进行分组也主要是为了使模型更轻量级，减少计算量

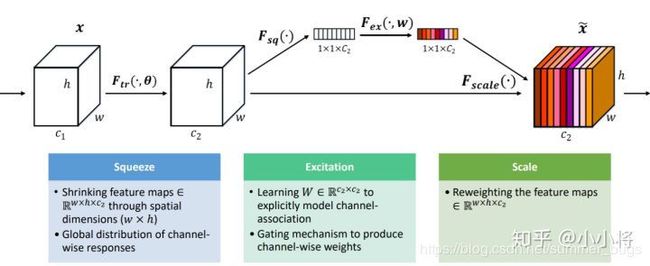
而SeNet网络的创新点在于，关注channel之间的关系，希望模型可以自动学习到不同channel特征的重要程度，为此，SENet提出了Squeeze-and-Excitation(SE)模块，如下图

SE模块首先对得到的特征图进行Squeeze操作，得到channel级的全局特征，然后对全局特征进行Excitation操作，学习各个channel之间的关系，也得到不同channel的权重，最后乘以原来的特征图得到最终特征

本质上，SE模块实在channel维度上做attention或者gating操作，这种注意力机制让模型可以更加关注信息量最大的channel特征，进而抑制哪些不重要的channel特征。另外，SE模块是通用的，这意味着可以嵌入到现有的网络框架中

SE模块

以普通的卷积为例

$F_{tr}:X\to U,X\in R^{H^{\prime }\ast W^{\prime }\ast C^{\prime }},U\in R^{H\ast W\ast C}$，卷积核为$V=[v_1,v_2,...,v_C]$，其中$v_c$表示第c个卷积核，那么输出$U=[u_1,u_2,...,u_C]$

$u_c=v_{c}X={\sum }_{s=1}^{C^{\prime }}{v}_c^8{x}^8$，其中$v_c^8$代表一个3D卷积核，器输入一个channel上的空间特征，它学习特征空间关系，但是由于对各个channel的卷积结果做了求和，所以channel特征关系与卷积核学习到的空间关系混合在了一起，而SE模块就是为了抽离这种混杂，使得模型直接学习到channel特征关系

• Squeeze操作

  由于卷积只是在一个局部空间内进行操作，U很难获得足够的信息来提取channel之间的关系，对于网络中前面的层会更加严重，因为感受野比较小，因此，SENet提出Squeeze操作，将一个channel上整个空间特征编码为一个全局特征，采用GlobalAveragePooling来实现（原则上也可用更复杂的聚合策略

• Excitation操作

  上面的Squeeze操作得到了全局描述特征，然而，我们需要得到各个channel之间的关系。这个操作需要满足两个准则：

  • 1.要灵活，它可以学习到各个channel之间的非线性关系

  • 2.学习关系不是互斥的，因为这里允许多channel特征，而不是one-hot形式，基于此，这里采用sigmoid形式的gating机制：

    $s=F_{ex}(z,W)=\sigma (g(z,W))=\sigma (W_{2}ReLU(W_{1}z))$

    其中$W_1\in R^{\frac{C}{r}\ast C},W_2\in R^{C\ast \frac{C}{r}}$，为了降低模型的复杂度以及提升泛化能力，这里采用了两个全连接层的bottleneck结构，其中第一个FC层起到降维的作用，降维系数是r个超参数，然后采用ReLU激活，最后的FC层恢复原始的维度

    最后将学习到的各个channel的激活值（sigmoid激活，在[0,1]之间）乘以U上的原始特征

    $\tilde{x}c=Fscale(u_c,s_c)=s_c\cdot u_c$

    其实整个操作可以看成学习到了各个channel的权重系数，从而使得模型对各个channel的特征更有辨别能力，这应该也算一种attention机制

SE-Inception Module的代码实现

# SE-Inception Module实现
def build_model(output_dims,input_shape=(224,224,3)):
    inputs_dim = Input(input_shape)
    x = Lambda(lambda x: x / 255.0)(inputs_dim) # 归一化处理
    
    x = InceptionV3(include_top=False,
                               weights="imagenet",
                               input_tensor=None,
                               input_shape=(224,224,3),
                               pooling=max)(x)
    
    squeeze = GlobalAveragePooling2D()(x)
    
    excitation = Dense(units=2048//11)(squeeze)
    excitation = Activation("relu")(excitation)
    excitation  = Dense(units=2048)(excitation)
    excitation = Activation("sigmoid")(excitation)
    excitation = Reshape((1,1,2048))(excitation)
    
    scale = multiply([x,excitation])
    
    x = GlobalAveragePooling2D()(scale)
    dp_1 = Dropout(0.6)(x)
    fc2 = Dense(out_dims)(dp_1)
    fc2 = Activation("sigmoid")(fc2)
    model = Model(inputs=inputs_dim,outputs=fc2)
    return model

8.CBAM

SENet是在feature map的通道上进行attention生成，然后与原来的feature map相乘

CBAM中，将attention同时运用到channel和spatial（空间）两个维度上，同样的，CBAM也可以嵌入到目前大部分主流网络中，在不显著增加计算量和参数量的前提下提升网络模型的特征提取能力

可以看到，一个CBAM包括两个子模块，分别进行通道上和空间上的attention，通道上的attention可以追溯到SENet，空间上的attention则更早，两个attention模块最后也都是使用sigmoid来缩放到[0,1]之间

• channel attention Module

  将输入的feature map分别经过基于width和height的GlobalMaxPooling 和GlobalAveragePooling，然后分别经过MLP（Multilayer Perceptron，多层感知机），将MLP输出的特征进行基于element wise的加和操作，最后再经过sigmoid激活，生成最终的channel attention feature map。将该channel attention feature map和input feature map做element wise乘法（同位元素对应相乘）操作，生成spatial attention模块需要的输入特征

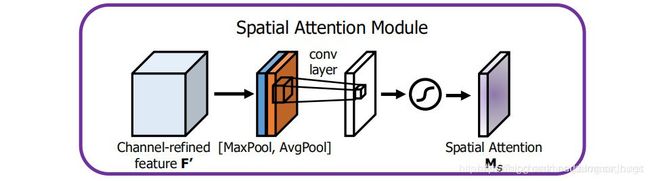
• Spatial attention module

  将channel attention模块输出的特征图作为本模块的输入特征图

  首先做一个基于channel的GlobalMaxPooling和GlobalAveragePooling，然后这两个结果基于channel做concatenate操作，然后经过一个卷机操作，降维为1个channel，再经过sigmoid生成spatial attention feature，最后将该feature 和该模块输入的feature做乘法，得到最终生成的特征

CBAM模块的实现

def CBAM(input,reduction):
    """
    @Convolutional Block Attention Module
    """
    _, width, height, channel = input.get_shape()  # (B,W,H,C)
    
    # channel attention
    x_mean = tf.reduce_mean(input,axis=(1,2).keepdims=True)   # (B,1,1,C)
    x_mean = tf.layers.conv2d(x_mean, channel // reduction, 1, activation=tf.nn.relu, name="CA1") # (B,1,1,C/r)
    x_mean = tf.layers.conv2d(x_mean, channel, 1, name="CV2") # (B,1,1,C)
    
    x_max = tf.reduce_max(input,axis=(1,2),keepdims=True) # (B,1,1,C)
    x_max = tf..layers.conv2d(x_max,channel//reduction,1,activation=tf.nn.relu,name="CA1",reuse=True) #(B,1,1,C//r)
    x_max = tf.layers.conv2d(x_max,channel,1,name="CA2",reuse=True) # (B,1,1,C) # reuse：Boolean类型，表示是否可以重复使用具有相同名字的前一层的权重。
    
    x = tf.add(x_mean,x_max) # (B,1,1,C)
    x = tf.nn.sigmoid(x) # (B,1,1,C)
    x= tf.multiply(input,x) #(B,W,H,C)
    
    # spatial attention
    y_mean = tf.reduce_mean(x,axis=3,keepdims=True) # (B,W,H,1)
    y_max = tf.reduce_max(x,axis=3,keepdims=True) # (B,W,H,1)
    y = tf.concat([y_mean,y_max],axis=-1) # (B,W,H,2)
    y = tf.layers.conv2d(y,1,7,padding="same",activation=tf.nn.sigmoid) # (B,W,H,1)
    y = tf.multiply(x,y) # (B,W,H,C)
    
    return y

ut,axis=(1,2),keepdims=True) # (B,1,1,C)
x_max = tf…layers.conv2d(x_max,channel//reduction,1,activation=tf.nn.relu,name=“CA1”,reuse=True) #(B,1,1,C//r)
x_max = tf.layers.conv2d(x_max,channel,1,name=“CA2”,reuse=True) # (B,1,1,C) # reuse：Boolean类型，表示是否可以重复使用具有相同名字的前一层的权重。

x = tf.add(x_mean,x_max) # (B,1,1,C)
x = tf.nn.sigmoid(x) # (B,1,1,C)
x= tf.multiply(input,x) #(B,W,H,C)

# spatial attention
y_mean = tf.reduce_mean(x,axis=3,keepdims=True) # (B,W,H,1)
y_max = tf.reduce_max(x,axis=3,keepdims=True) # (B,W,H,1)
y = tf.concat([y_mean,y_max],axis=-1) # (B,W,H,2)
y = tf.layers.conv2d(y,1,7,padding="same",activation=tf.nn.sigmoid) # (B,W,H,1)
y = tf.multiply(x,y) # (B,W,H,C)

return y