CS229第一课——线性回归

线性回归

我们以下方的一个例子来讲解线性回归过程。

在该例子中，输入数据$x$是一个二维变量，$x_1^{(i)}$代表第$i$个数据样本中的第一个特征值(在实际情况中我们需要自己来选择进行训练的特征数，我们会在之后讲解特征选择的方法，目前该例子中使用2个特征进行学习)。
为了进行学习，我们需要定义一个hypothesis，我们使用$\mathbf{x}$的线性方程来近似$y$，如下所示
$$y={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2$$
在此处$\theta$是一个参数（权重）用来将输入的数据$\mathbf{x}$映射到输出$y$。为了方便编写，我们定义$x_0=1$，则上式可以修改为
$$y=\sum _{i=1}^n{\theta }_i{x}_i={\theta }^T\mathbf{x}$$
接下来，为了学习合适的参数$\theta$，我们需要定义一个损失函数来描述预测值与实际值之间的距离，定义如下
$$J=\frac{1}{2}\sum _{i=1}^m(h(x^i)-y^i{)}^2$$

1 LMS算法

我们需要学习一个参数向量$\theta$来最小化损失函数$J(\theta )$，我们一般使用梯度下降法来学习$\theta$值，该算法学习过程如下所示
$${\theta }_j={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J(\theta )$$
为了方便描述，我们首先假设训练数据集中只有一个样本，则训练的梯度下降如下所示。
$$\begin{array}{rl}{\theta }_j& ={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J(\theta )\\ & ={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}(\frac{1}{2}(h(x)-y{)}^2)\\ & ={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}(\frac{1}{2}(\sum _{i=1}^n{\theta }_i{x}_i-y{)}^2)\\ & ={\theta }_j-\alpha (\sum _{i=1}^n{\theta }_i{x}_i-y{)}^2{x}_j\end{array}$$
这个更新规则称为LMS（最小均方误差），一般有两种方法来应用该规则。
一种是批量梯度下降，每一次更新参数值都需要应用所有的数据样本，如下所示。

梯度下降算法容易收敛到局部最优值，而在线性回归中，损失函数是凸函数，只存在一个全局最优值，因此能实现较好的收敛效果。
第二种应用LMS规则的方法是随机梯度下降，每利用一个数据样本就更新一次参数值，具体情况如下所示。

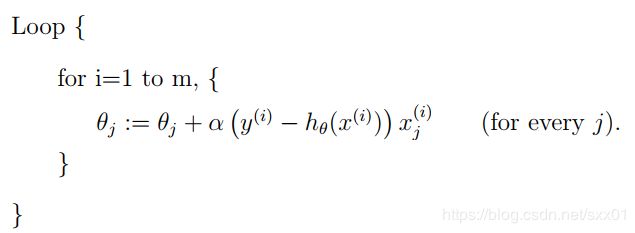
如果数据样本数量非常大，则批量梯度下降的更新速度太慢，随机梯度下降每针对一个样本就更新一次，因此能快速对参数进行更新，通常会比批量梯度下降更快收敛的“靠近”全局最优的位置，但一般不会收敛到最优值处。

2 正规方程

接下来考虑第二种方法来最小化损失函数$J$，这种方法是通过将损失函数对应的${\theta }_j$的导数值设为0来求解$\theta$，为了介绍该方法，我们需要定义一些矩阵微积分符号。

2.1 矩阵微积分

定义一个函数$f$，该函数能将一个$m\times n$的矩阵映射成一个实数，我们定义函数$f$关于矩阵$A$的微积分如下。
$${\nabla }_{A}f(A)=\left[\begin{array}{ccc}\frac{\partial f}{\partial A_{11}}& \cdots & \frac{\partial f}{\partial A_{1n}}\\ ⋮& \ddots & ⋮\\ \frac{\partial f}{\partial A_{m1}}& \cdots & \frac{\partial f}{\partial A_{mn}}\end{array}\right]$$
接下来我们定义trace计算，即
$$trA=\sum _{i=1}^n{A}_{ii}$$
如果我们有矩阵$A$和$B$，且$AB$是一个方阵，则$trAB=trBA$
证明：令$A$为$m\times n$的矩阵，$B$为$n\times m$的矩阵，则$AB$为$m\times m$的矩阵，$BA$为$n\times n$的矩阵，令$AB=C$，$AB=D$，因此
$$\begin{array}{rl}trAB& =\sum _{i=1}^m{C}_{ii}\\ & =\sum _{i=1}^m(\sum _{j=1}^n(A_{ij}{B}_{ji}))\\ trBA& =\sum _{i=1}^n{D}_{ii}\\ & =\sum _{j=1}^n(\sum _{i=1}^m(A_{ij}{B}_{ji}))\end{array}$$
因此$trAB=trBA$，证毕。
有这个推论我们可以得出
$$trABC=trCAB=trBCA$$
此外trace计算还有以下的性质：
$$\begin{gathered} tr{A}^T=trA \\ tr(A+B)=trA+trB \\ traA=atrA \end{gathered}$$
矩阵微积分有着以下的性质，其中|$A$|代表$A$的行列式
$$\begin{array}{rl}{\nabla }_{A}trAB& =B^T\\ {\nabla }_{A^T}f(A)& =({\nabla }_{A}f(A){)}^T\\ {\nabla }_{A}trAB{A}^{T}C& =CBA+C^{T}A{B}^T\\ {\nabla }_A|A|& =|A|(A^{-1}{)}^T\end{array}$$

2.2 最小二乘新解释

利用上述提到的矩阵微积分来对最小二乘进行求解，我们首先将损失函数$J(\theta )$写成矩阵-向量格式。
对于给定的数据集，我们将其定义为$m\times n$的矩阵$\mathbf{X}$，该矩阵为
$$\mathbf{X}=\left[\begin{array}{c}(x^{(1)}{)}^T\\ (x^{(2)}{)}^T\\ ⋮\\ (x^{(m)}{)}^T\end{array}\right]$$
并且将标签数据定义为m维的向量$\mathbf{Y}$,该向量为
$$\mathbf{Y}=\left[\begin{array}{c}(y^{(1)})\\ (y^{(2)})\\ ⋮\\ (y^{(m)})\end{array}\right]$$
则
$$\mathbf{X}\theta -\mathbf{Y}=\left[\begin{array}{c}{h}_{\theta }(x^{(1)})-y^{(1)}\\ h_{\theta }(x^{(2)})-y^{(2)}\\ ⋮\\ h_{\theta }(x^{(m)})-y^{(m)}\end{array}\right]$$
损失函数定义为
$$J(\theta )=\frac{1}{2}(\mathbf{X}\theta -\mathbf{Y}{)}^T(\mathbf{X}\theta -\mathbf{Y})$$
因此
$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )& ={\nabla }_{\theta }(\frac{1}{2}(\mathbf{X}\theta -\mathbf{Y}{)}^T(\mathbf{X}\theta -\mathbf{Y}))\\ & =\frac{1}{2}{\nabla }_{\theta }({\theta }^T{\mathbf{X}}^T\mathbf{X}\theta -{\theta }^T{\mathbf{X}}^T\mathbf{Y}-{\mathbf{Y}}^T\mathbf{X}\theta +{\mathbf{Y}}^T\mathbf{Y})\\ & =\frac{1}{2}{\nabla }_{\theta }tr({\theta }^T{\mathbf{X}}^T\mathbf{X}\theta -{\theta }^T{\mathbf{X}}^T\mathbf{Y}-{\mathbf{Y}}^T\mathbf{X}\theta +{\mathbf{Y}}^T\mathbf{Y})\\ & =\frac{1}{2}({\nabla }_{\theta }tr({\theta }^T{\mathbf{X}}^T\mathbf{X}\theta )-2{\nabla }_{\theta }tr{\mathbf{Y}}^T\mathbf{X}\theta )\\ & =\frac{1}{2}({\mathbf{X}}^T\mathbf{X}\theta +{\mathbf{X}}^T\mathbf{X}\theta -2{\mathbf{X}}^{\mathbf{T}}\mathbf{Y})\\ & ={\mathbf{X}}^T\mathbf{X}\theta -{\mathbf{X}}^{\mathbf{T}}\mathbf{Y}\end{array}$$
令该微分式为0，则${\mathbf{X}}^T\mathbf{X}\theta -{\mathbf{X}}^{\mathbf{T}}\mathbf{Y}=0$，可以得到
$$\theta =({\mathbf{X}}^T\mathbf{X}{)}^{-1}{\mathbf{X}}^T\mathbf{Y}$$

3 概率解释

在进行线性回归训练的时候，为什么使用最小二乘作为损失函数？我们将会给出一些概率假设进行解释。
我们假设标签$y$的值为$y^{(i)}={\theta }^T{x}^{(i)}+ϵ$，其中第一项为我们的预测值，第二项为错误项（代表忽略的特征项或者随机噪声）。我们假设错误项$ϵ$的分布符合IID特点，并且符合均值为0、方差为${\sigma }^2$，因此${ϵ}^{(i)}$的概率密度为
$$p({ϵ}^{(i)})=\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{({ϵ}^{(i)}{)}^2}{2{\sigma }^2})$$
给定输入数据$x^{(i)}$和权重$\theta$后，可以得到
$$p(y^{(i)}|x^{(i)};\theta )=\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})$$
该式中$p(y^{(i)}|x^{(i)};\theta )$代表给定$x^{(i)}$并由权重$\theta$参数化的分布$y^{(i)}$，我们同样可以将$y^{(i)}$的分布写为$y^{(i)}|x^{(i)};\theta \sim \mathcal{N}({\theta }^T{x}^{(i)},{\sigma }^2)$。
当给定输入矩阵$\mathbf{X}$和参数$\theta$后，关于输出数据$\mathbf{Y}$的概率给定为$p(\mathbf{Y}|\mathbf{X};\theta )$，当给定参数$\theta$后，将该式定义为$\mathbf{Y}$的函数。当我们将其视为关于$\theta$的函数时，我们将其称为似然函数，定义为
$$L(\theta )=L(\theta ;\mathbf{X},\mathbf{Y})=p(\mathbf{Y}|\mathbf{X};\theta )$$
由于我们将错误项${ϵ}^{(i)}$定义为独立分布，因此可以得到
$$\begin{array}{rl}L(\theta )& =\prod _{i=1}^{m}p(y^{(i)}|x^{(i)};\theta )\\ & =\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})\end{array}$$
在训练模型的时候，给定了输入数据$\mathbf{X}$和标签数据$\mathbf{Y}$，我们需要通过将该似然函数进行最大化，使给定的数据以最大的概率出现，从而选择合适的参数$\theta$。为了使得求解方便，我们给似然函数增加一个对数操作，这样不会改变其递增性质，也方便求解，具体如下所示
$$\begin{array}{rl}l(\theta )& =logL(\theta )\\ & =log\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})\\ & =\sum _{i=1}^{m}log\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})\\ & =\sum _{i=1}^m(log\frac{1}{\sqrt{2\pi }\sigma }-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})\\ & =mlog\frac{1}{\sqrt{2\pi }\sigma }-\frac{1}{{\sigma }^2}\frac{1}{2}\sum _{i=1}^m(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2\end{array}$$
由于在上式中，第一项是定项，因此我们需要最小化第二项，也就是最小化$\frac{1}{2}{\sum }_{i=1}^m(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2$，因此我们将线性回归中的损失函数定义为最小二乘。
总结：给定了上述关于数据分布的假设后，线性回归的最小二乘对应于最大似然函数，因此使用最小二乘作为线性回归的损失函数是一种自然的选择。在我们之前的讨论中，我们训练的参数$\theta$并不依赖于分布的方差${\sigma }^2$，即使该方差是未知的结果也不会变化。

4 局部加权线性回归

如上图所示，不同的特征选择会导致我们训练出来的模型的性能表现不同，左侧的图属于欠拟合，右侧的图属于过拟合，在之后我们会详细介绍这些概念并且介绍自动选择特征的算法，在本节中，我们会介绍局部加权线性回归（LWR）算法，该算法假设有足够多的数据样本，那么特征的选择就不是很重要了。
在局部加权线性回归中，给定$x$进行预测时，我们需要

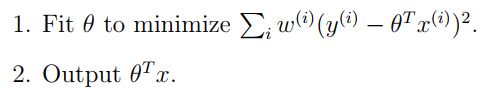
其中的$w^{(i)}$是一个非负的权重值，该值的大小决定了我们对于错误项$(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2$的重视程度，我们一般将该值定义为
$$w^{(i)}=exp(-\frac{(x^{(i)}-x{)}^2}{2{\tau }^2})$$
当训练的数据点与要预测的点接近时，该权重值趋近于1，否则趋近于0，因此对于接近的点的重视程度会比较高。参数$\tau$用来控制训练样本随着点$x^{(i)}$与预测点$x$的距离下降快慢的程度，称为带宽参数。
局部加权线性回归属于非参数算法，表示在使用该算法进行预测的时候，我们需要保留整个训练集；而之前学习的线性回归属于参数化算法，因为一旦参数固定后我们不需要再使用训练数据集。