独家 | 从基础到实现：集成学习综合教程（附Python代码）

作者：AISHWARYA SINGH

翻译：和中华

校对：丁楠雅

本文约8000字，建议阅读10+分钟。

本文从基础集成技术讲起，随后介绍了高级的集成技术，最后特别介绍了一些流行的基于Bagging和Boosting的算法，帮助读者对集成学习建立一个整体印象。

介绍

当你想购买一辆新车时，你会走到第一家汽车商店就根据经销商的建议购买一辆车吗？这是不太可能的。

 

你可能会浏览一些人们发布评论并比较不同车型的门户网站，检查其功能和价格。你也可能会问你的朋友和同事们的意见。总之，你不会直接得出结论，还会参考其他人的意见做出决定。

机器学习中的集成模型也是类似的思路。它们结合了多个模型的决策来提高整体性能。这可以通过各种方式实现，本文将会带你一起探索。

 

本文的目的是介绍集成学习的概念并理解使用这种技术的算法。为了巩固你对这个多元化主题的理解，我们将用真实问题的动手案例，配合Python来解释其中的高级算法。

 

注意：本文假定你对机器学习算法有基本的了解。我建议阅读这篇文章以熟悉这些概念。

文章链接：

https://www.analyticsvidhya.com/blog/2017/09/common-machine-learning-algorithms/

 

目录

• 集成学习介绍

• 基础集成技术

• • 最大投票（Max Voting）法

  • 平均（Averaging）法

  • 加权平均（Weighted Average）法

• 高级集成技术

• • 堆叠（Stacking）

  • 混合（Blending）

  • Bagging

  •  提升（Boosting）

• 基于Bagging和Boosting的算法

• • Bagging meta-estimator

  • 随机森林

  • AdaBoost

  • GBM

  • XGB

  • Light GBM

  • CatBoost

 

一、集成学习介绍

我们通过一个例子来理解集成学习的概念。假设你是一名电影导演，你依据一个非常重要且有趣的话题创作了一部短片。现在，你想在公开发布前获得影片的初步反馈（评级）。有哪些可行的方法呢？

 

A：可以请一位朋友为电影打分。

于是完全有可能出现这种结果：你所选择的人由于非常爱你，并且不希望给你这部糟糕的影片打1星评级来伤害你脆弱的小心脏。

 

B：另一种方法是让你的5位同事评价这部电影。

这个办法应该更好，可能会为电影提供更客观诚实的评分。但问题依然存在。这5个人可能不是电影主题方面的“专家”。当然，他们可能懂电影摄制，镜头或音效，但他们可能并不是黑色幽默的最佳评判者。

 

C：让50个人评价这部电影呢？

其中一些可以是你的朋友，可以是你的同事，甚至是完完全全的陌生人。

 

在这种情况下，回应将更加普遍化和多样化，因为他们拥有不同的技能。事实证明，与我们之前看到的情况相比，这是获得诚实评级的更好方法。

 

通过这些例子，你可以推断，与个人相比，不同群体的人可能会做出更好的决策。与单一模型相比，各种不同模型也是这个道理。机器学习中的多样化是通过称为集成学习（Ensemble learning）的技术实现的。

 

现在你已经掌握了集成学习的要旨，接下来让我们看看集成学习中的各种技术及其实现。

二、简单集成技术

这一节中，我们会看一些简单但是强大的技术，比如：

 

• 最大投票法

• 平均法

• 加权平均法

 

2.1 最大投票法

最大投票方法通常用于分类问题。这种技术中使用多个模型来预测每个数据点。每个模型的预测都被视为一次“投票”。大多数模型得到的预测被用作最终预测结果。

 

例如，当你让5位同事评价你的电影时（最高5分）; 我们假设其中三位将它评为4，而另外两位给它一个5。由于多数人评分为4，所以最终评分为4。你可以将此视为采用了所有预测的众数（mode）。

 

最大投票的结果有点像这样：

示例代码：

 

这里x_train由训练数据中的自变量组成，y_train是训练数据的目标变量。验证集是x_test（自变量）和y_test（目标变量）。

 

model1 = tree.DecisionTreeClassifier()

model2 = KNeighborsClassifier()

model3= LogisticRegression()

 

model1.fit(x_train,y_train)

model2.fit(x_train,y_train)

model3.fit(x_train,y_train)

 

pred1=model1.predict(x_test)

pred2=model2.predict(x_test)

pred3=model3.predict(x_test)

 

final_pred = np.array([])

for i in range(0,len(x_test)):

    final_pred =np.append(final_pred, mode([pred1[i], pred2[i], pred3[i]]))

 

或者，你也可以在sklearn中使用“VotingClassifier”模块，如下所示：

 

from sklearn.ensemble import VotingClassifier

model1 = LogisticRegression(random_state=1)

model2 = tree.DecisionTreeClassifier(random_state=1)

model = VotingClassifier(estimators=[('lr', model1), ('dt', model2)], voting='hard')

model.fit(x_train,y_train)

model.score(x_test,y_test)

 

2.2 平均法

类似于最大投票技术，这里对每个数据点的多次预测进行平均。在这种方法中，我们从所有模型中取平均值作为最终预测。平均法可用于在回归问题中进行预测或在计算分类问题的概率时使用。

 

例如，在下面的情况中，平均法将取所有值的平均值。

 

即（5 + 4 + 5 + 4 + 4）/ 5 = 4.4

 

示例代码：

model1 = tree.DecisionTreeClassifier()

model2 = KNeighborsClassifier()

model3= LogisticRegression()

 

model1.fit(x_train,y_train)

model2.fit(x_train,y_train)

model3.fit(x_train,y_train)

 

pred1=model1.predict_proba(x_test)

pred2=model2.predict_proba(x_test)

pred3=model3.predict_proba(x_test)

 

finalpred=(pred1+pred2+pred3)/3

 

2.3 加权平均法

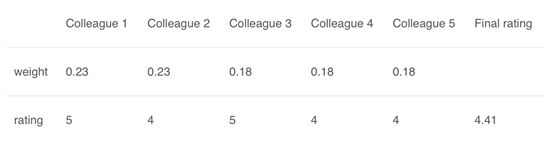
这是平均法的扩展。为所有模型分配不同的权重，定义每个模型的预测重要性。例如，如果你的两个同事是评论员，而其他人在这方面没有任何经验，那么与其他人相比，这两个朋友的答案就更加重要。

 

计算结果为[（5 * 0.23）+（4 * 0.23）+（5 * 0.18）+（4 * 0.18）+（4 * 0.18）] = 4.41。

 

示例代码：

model1 = tree.DecisionTreeClassifier()

model2 = KNeighborsClassifier()

model3= LogisticRegression()

 

model1.fit(x_train,y_train)

model2.fit(x_train,y_train)

model3.fit(x_train,y_train)

 

pred1=model1.predict_proba(x_test)

pred2=model2.predict_proba(x_test)

pred3=model3.predict_proba(x_test)

 

finalpred=(pred1*0.3+pred2*0.3+pred3*0.4)

 

三、高级集成技术

我们已经介绍了基础的集成技术，让我们继续了解高级的技术。

3.1 堆叠（Stacking）

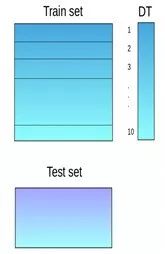
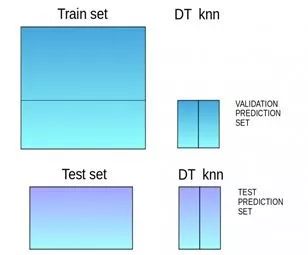
堆叠是一种集成学习技术，它使用多个模型（例如决策树，knn或svm）的预测来构建新模型。该新模型用于对测试集进行预测。以下是简单堆叠集成法的逐步解释：

 

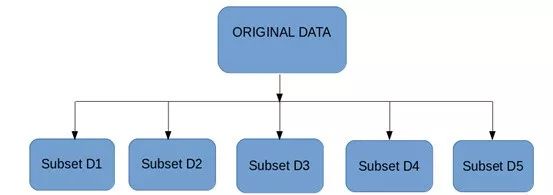
第一步：把训练集分成10份

 

第二步：基础模型（假设是决策树）在其中9份上拟合，并对第10份进行预测。

第三步：对训练集上的每一份如此做一遍。

第四步：然后将基础模型（此处是决策树）拟合到整个训练集上。

第五步：使用此模型，在测试集上进行预测。

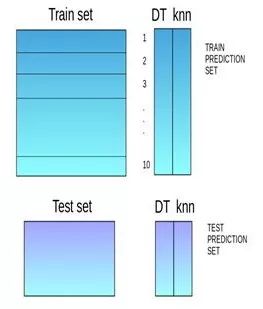
第六步：对另一个基本模型（比如knn）重复步骤2到4，产生对训练集和测试集的另一组预测。

第七步：训练集预测被用作构建新模型的特征。

第八步：该新模型用于对测试预测集（test prediction set，上图的右下角）进行最终预测。

 

示例代码：

 

我们首先定义一个函数来对n折的训练集和测试集进行预测。此函数返回每个模型对训练集和测试集的预测。

def Stacking(model,train,y,test,n_fold):

   folds=StratifiedKFold(n_splits=n_fold,random_state=1)

   test_pred=np.empty((test.shape[0],1),float)

   train_pred=np.empty((0,1),float)

   for train_indices,val_indices in folds.split(train,y.values):

      x_train,x_val=train.iloc[train_indices],train.iloc[val_indices]

      y_train,y_val=y.iloc[train_indices],y.iloc[val_indices]

 

      model.fit(X=x_train,y=y_train)

      train_pred=np.append(train_pred,model.predict(x_val))

      test_pred=np.append(test_pred,model.predict(test))

    return test_pred.reshape(-1,1),train_pred

现在我们将创建两个基本模型：决策树和knn。

model1 = tree.DecisionTreeClassifier(random_state=1)

 

test_pred1 ,train_pred1=Stacking(model=model1,n_fold=10, train=x_train,test=x_test,y=y_train)

 

train_pred1=pd.DataFrame(train_pred1)

test_pred1=pd.DataFrame(test_pred1)

 

model2 = KNeighborsClassifier()

 

test_pred2 ,train_pred2=Stacking(model=model2,n_fold=10,train=x_train,test=x_test,y=y_train)

 

train_pred2=pd.DataFrame(train_pred2)

test_pred2=pd.DataFrame(test_pred2)

创建第三个模型，逻辑回归，在决策树和knn模型的预测之上。

df = pd.concat([train_pred1, train_pred2], axis=1)

df_test = pd.concat([test_pred1, test_pred2], axis=1)

 

model = LogisticRegression(random_state=1)

model.fit(df,y_train)

model.score(df_test, y_test)

为了简化上面的解释，我们创建的堆叠模型只有两层。决策树和knn模型建立在零级，而逻辑回归模型建立在第一级。其实可以随意的在堆叠模型中创建多个层次。

3.2 混合（Stacking）

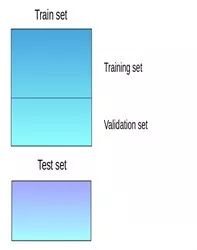
混合遵循与堆叠相同的方法，但仅使用来自训练集的一个留出(holdout)/验证集来进行预测。换句话说，与堆叠不同，预测仅在留出集上进行。留出集和预测用于构建在测试集上运行的模型。以下是混合过程的详细说明：

 

第一步：原始训练数据被分为训练集合验证集。

 

第二步：在训练集上拟合模型。

第三步：在验证集和测试集上进行预测。

第四步：验证集及其预测用作构建新模型的特征。

第五步：该新模型用于对测试集和元特征(meta-features)进行最终预测。

 

示例代码：

 

我们将在训练集上建立两个模型，决策树和knn，以便对验证集进行预测。

model1 = tree.DecisionTreeClassifier()

model1.fit(x_train, y_train)

val_pred1=model1.predict(x_val)

test_pred1=model1.predict(x_test)

val_pred1=pd.DataFrame(val_pred1)

test_pred1=pd.DataFrame(test_pred1)

 

model2 = KNeighborsClassifier()

model2.fit(x_train,y_train)

val_pred2=model2.predict(x_val)

test_pred2=model2.predict(x_test)

val_pred2=pd.DataFrame(val_pred2)

test_pred2=pd.DataFrame(test_pred2)

结合元特征和验证集，构建逻辑回归模型以对测试集进行预测。

df_val=pd.concat([x_val, val_pred1,val_pred2],axis=1)

df_test=pd.concat([x_test, test_pred1,test_pred2],axis=1)

 

model = LogisticRegression()

model.fit(df_val,y_val)

model.score(df_test,y_test)

3.3 Bagging

Bagging背后的想法是结合多个模型的结果（例如，所有决策树）来获得泛化的结果。这有一个问题：如果在同样一组数据上创建所有模型并将其组合起来，它会有用吗？这些模型极大可能会得到相同的结果，因为它们获得的输入相同。那我们该如何解决这个问题呢？其中一种技术是自举(bootstrapping)。

 

Bootstrapping是一种采样技术，我们有放回的从原始数据集上创建观察子集，子集的大小与原始集的大小相同。

 

Bagging（或Bootstrap Aggregating）技术使用这些子集（包）来获得分布的完整概念（完备集）。为bagging创建的子集的大小也可能小于原始集。

 

第一步：从原始数据集有放回的选择观测值来创建多个子集。

第二步：在每一个子集上创建一个基础模型（弱模型）。

第三步：这些模型同时运行，彼此独立。

第四步：通过组合所有模型的预测来确定最终预测。

 

3.4 Boosting

在我们进一步讨论之前，这里有另一个问题：如果第一个模型错误地预测了某一个数据点，然后接下来的模型（可能是所有模型），将预测组合起来会提供更好的结果吗？Boosting就是来处理这种情况的。

 

Boosting是一个顺序过程，每个后续模型都会尝试纠正先前模型的错误。后续的模型依赖于之前的模型。接下来一起看看boosting的工作方式：

 

第一步：从原始数据集创建一个子集。

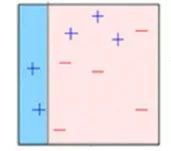
第二步：最初，所有数据点都具有相同的权重。

第三步：在此子集上创建基础模型。

第四步：该模型用于对整个数据集进行预测。

 

第五步：使用实际值和预测值计算误差。

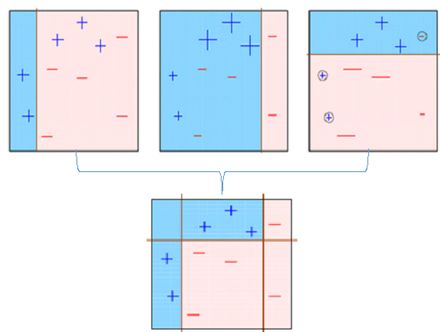
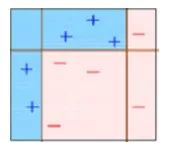
第六步：预测错误的点获得更高的权重。（这里，三个错误分类的蓝色加号点将被赋予更高的权重）

第七步：创建另一个模型并对数据集进行预测（此模型尝试更正先前模型中的错误）。

第八步：类似地，创建多个模型，每个模型校正先前模型的错误。

第九步：最终模型（强学习器）是所有模型（弱学习器）的加权平均值。

因此，boosting算法结合了许多弱学习器来形成一个强学习器。单个模型在整个数据集上表现不佳，但它们在数据集的某些部分上表现很好。因此，每个模型实际上提升了集成的整体性能。

 

四、基于Bagging和Boosting的算法

Bagging和Boosting是机器学习中最常用的两种技术。在本节中，我们将详细介绍它们。以下是我们将关注的算法：

Bagging 算法:

• Bagging meta-estimator

• 随机森林

 

Boosting算法：

• AdaBoost

• GBM

• XGBM

• Light GBM

• CatBoost

 

对于本节中讨论的所有算法，我们将遵循以下顺序：

• 算法介绍

• 示例代码

• 参数

 

本文中，我使用了贷款预测问题。你可以从此处下载数据集。请注意，对于每种算法，某些代码（读取数据，划分训练测试集等）将是相同的。为了避免重复，我在下面编写了相同的代码，并且只对算法相关的代码进行进一步讨论。

#importing important packages

import pandas as pd

import numpy as np

 

#reading the dataset

df=pd.read_csv("/home/user/Desktop/train.csv")

 

#filling missing values

df['Gender'].fillna('Male', inplace=True)

同理，对所有列进行值填充。本文只考虑所讨论的主题，已跳过EDA，缺失值和异常值处理等步骤。要了解这些主题，可以阅读此文：Ultimate guide for Data Explorationin Python using NumPy, Matplotlib and Pandas.

 

#split dataset into train and test

 

from sklearn.model_selection import train_test_split

train, test = train_test_split(df, test_size=0.3, random_state=0)

 

x_train=train.drop('Loan_Status',axis=1)

y_train=train['Loan_Status']

 

x_test=test.drop('Loan_Status',axis=1)

y_test=test['Loan_Status']

 

#create dummies

x_train=pd.get_dummies(x_train)

x_test=pd.get_dummies(x_test)

让我们来探索bagging和boosting算法。

 

4.1 Bagging meta-estimator

Bagging meta-estimator是一种集成算法，可用于分类(BaggingClassifier)和回归(BaggingRegressor)问题。它采用典型的bagging技术进行预测。以下是Bagging meta-estimator算法的步骤：

 

第一步：从原始数据集（Bootstrapping）创建随机子集。

第二步：数据集的子集包括所有特征。

第三步用户指定的基础估计器在这些较小的集合上拟合。

第四步：将每个模型的预测结合起来得到最终结果。

 

示例代码：

from sklearn.ensemble import BaggingClassifier

from sklearn import tree

model = BaggingClassifier(tree.DecisionTreeClassifier(random_state=1))

model.fit(x_train, y_train)

model.score(x_test,y_test)

0.75135135135135134

 

回归问题示例代码：

from sklearn.ensemble import BaggingRegressor

model = BaggingRegressor(tree.DecisionTreeRegressor(random_state=1))

model.fit(x_train, y_train)

model.score(x_test,y_test)

算法中用到的参数：

• base_estimator

• • 定义了在随机子集上拟合所用的基础估计器

  • 没有指明时，默认使用决策树

• n_estimators

• • 创建的基础估计器数量

  • 要小心微调这个参数，因为数字越大运行时间越长，相反太小的数字可能无法提供最优结果

• max_samples

• • 该参数控制子集的大小

  • 它是训练每个基础估计器的最大样本数量

• max_features

• • 控制从数据集中提取多少个特征

  • 它是训练每个基础估计器的最大特征数量

• n_jobs

• • 同时运行的job数量

  • 将这个值设为你系统的CPU核数

  • 如果设为-1，这个值会被设为你系统的CPU核数

• random_state

• • 定义了随机分割的方法。当两个模型的random_state值一样时，它们的随机选择也一样

  • 如果你想对比不同的模型，这个参数很有用

 

4.2 随机森林

随机森林是另一种遵循bagging技术的集成机器学习算法。它是bagging-estimator算法的扩展。随机森林中的基础估计器是决策树。与bagging meta-estimator不同，随机森林随机选择一组特征，这些特征用于决定决策树的每个节点处的最佳分割。

 

随机森林的具体步骤如下:

 

第一步：从原始数据集（Bootstrapping）创建随机子集。

第二步：在决策树中的每个节点处，仅考虑一组随机特征来决定最佳分割。

第三步：在每个子集上拟合决策树模型。

第四步：通过对所有决策树的预测求平均来计算最终预测。

 

注意：随机林中的决策树可以构建在数据和特征的子集上。特别地，sklearn中的随机森林使用所有特征作为候选，并且候选特征的随机子集用于在每个节点处分裂。

 

总而言之，随机森林随机选择数据点和特征，并构建多个树（森林）。

 

示例代码：

from sklearn.ensemble import RandomForestClassifier

model= RandomForestClassifier(random_state=1)

model.fit(x_train, y_train)

model.score(x_test,y_test)

0.77297297297297296

你可以通过在随机林中使用model.feature_importances_来查看特征重要性。

for i, j in sorted(zip(x_train.columns, model.feature_importances_)):

    print(i, j)

结果如下：

ApplicantIncome 0.180924483743

CoapplicantIncome 0.135979758733

Credit_History 0.186436670523

.

.

.

Property_Area_Urban 0.0167025290557

Self_Employed_No 0.0165385567137

Self_Employed_Yes 0.0134763695267

回归问题示例代码：

from sklearn.ensemble import RandomForestRegressor

model= RandomForestRegressor()

model.fit(x_train, y_train)

model.score(x_test,y_test)

参数：

 

• n_estimators

• • 定义随机森林中要创建的决策树数量

  • 通常，越高的值会让预测更强大更稳定，但是过高的值会让训练时间很长

• criterion

• • 定义了分割用的函数

  • 该函数用来衡量使用每个特征分割的质量从而选择最佳分割

• max_features

• • 定义了每个决策树中可用于分割的最大特征数量

  • 增加最大特征数通常可以改善性能，但是一个非常高的值会减少各个树之间的差异性

• max_depth

• • 随机森林有多个决策树，此参数定义树的最大深度

• min_samples_split

• • 用于在尝试拆分之前定义叶节点中所需的最小样本数

  • 如果样本数小于所需数量，则不分割节点

• min_samples_leaf

• • 定义了叶子节点所需的最小样本数

  • 较小的叶片尺寸使得模型更容易捕获训练数据中的噪声

• max_leaf_nodes

• • 此参数指定每个树的最大叶子节点数

  • 当叶节点的数量变得等于最大叶节点时，树停止分裂

• n_jobs

• • 这表示并行运行的作业数

  • 如果要在系统中的所有核心上运行，请将值设置为-1

• random_state

• • 此参数用于定义随机选择

  • 它用于各种模型之间的比较

4.3 AdaBoost

自适应增强或AdaBoost是最简单的boosting算法之一。通常用决策树来建模。创建多个顺序模型，每个模型都校正上一个模型的错误。AdaBoost为错误预测的观测值分配权重，后续模型来正确预测这些值。

 

以下是执行AdaBoost算法的步骤：

第一步：最初，数据集中的所有观察值都具有相同的权重。

第二步：在数据子集上建立一个模型。

第三步：使用此模型，可以对整个数据集进行预测。

第四步：通过比较预测值和实际值来计算误差。

第五步：在创建下一个模型时，会给预测错误的数据点赋予更高的权重。

第六步：可以使用误差值确定权重。例如，误差越大，分配给观察值的权重越大。

第七步：重复该过程直到误差函数没有改变，或达到估计器数量的最大限制。

 

示例代码：

from sklearn.ensemble import AdaBoostClassifier

model = AdaBoostClassifier(random_state=1)

model.fit(x_train, y_train)

model.score(x_test,y_test)

0.81081081081081086

回归问题示例代码：

from sklearn.ensemble import AdaBoostRegressor

model = AdaBoostRegressor()

model.fit(x_train, y_train)

model.score(x_test,y_test)

参数：

 

• base_estimators

• • 它用于指定基础估计器的类型，即用作基础学习器的机器学习算法

• n_estimators

• • 它定义了基础估计器的数量

  • 默认值为10，但可以设为较高的值以获得更好的性能

• learning_rate

• • ‍此参数控制估计器在最终组合中的贡献

  • ‍在learning_rate和n_estimators之间需要进行权衡

• max_depth

• • 定义单个估计器的最大深度

  • 调整此参数以获得最佳性能

• n_jobs

• • 指定允许使用的处理器数

  • 将值设为-1，可以使用允许的最大处理器数量

• random_state

• • 用于指定随机数据拆分的整数值

  • 如果给出相同的参数和训练数据，random_state的确定值将始终产生相同的结果

 

4.4 Gradient Boosting（梯度提升GBM）

Gradient Boosting或GBM是另一种集成机器学习算法，适用于回归和分类问题。GBM使用boosting技术，结合了许多弱学习器，以形成一个强大的学习器。回归树用作基础学习器，每个后续的树都是基于前一棵树计算的错误构建的。

 

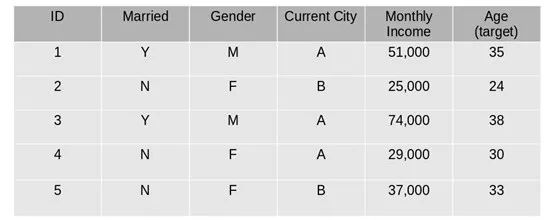
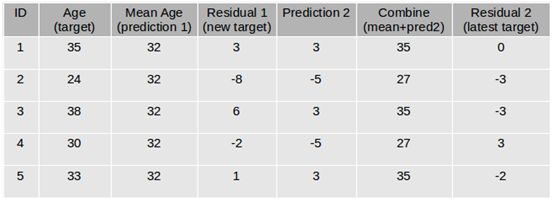
我们将使用一个简单的例子来理解GBM算法。我们会使用以下数据预测一群人的年龄：

第一步：假设平均年龄是数据集中所有观测值的预测值。

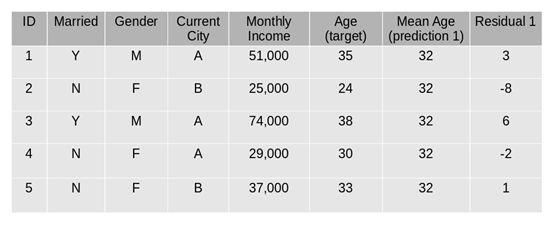
第二步：使用该平均预测值和年龄的实际值来计算误差：

第三步：使用上面计算的误差作为目标变量创建树模型。我们的目标是找到最佳分割以最小化误差。

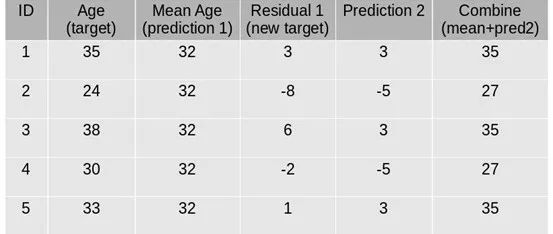
第四步：该模型的预测与预测1相结合：

第五步：上面计算的这个值是新的预测。

第六步：使用此预测值和实际值计算新误差：

 

 

第七步：重复步骤2到6，直到最大迭代次数（或误差函数不再改变）

 

示例代码：

from sklearn.ensemble import GradientBoostingClassifier

model= GradientBoostingClassifier(learning_rate=0.01,random_state=1)

model.fit(x_train, y_train)

model.score(x_test,y_test)

0.81621621621621621

回归问题示例代码：

from sklearn.ensemble import GradientBoostingRegressor

model= GradientBoostingRegressor()

model.fit(x_train, y_train)

model.score(x_test,y_test)

参数：

 

• min_samples_split

• • 定义考虑被拆分的节点中所需的最小样本数（或观察值数）

  • 用于控制过配合。较高的值会阻止模型学习关系，这种关系可能对为一棵树选择的特定样本高度特定

• min_samples_leaf

• • 定义终端或叶节点中所需的最小样本数

  • 一般来说，应该为不平衡的分类问题选择较低的值，因为少数群体占大多数的地区将非常小

• min_weight_fraction_leaf

• • ‍与min_samples_leaf类似，但定义为观察总数的一个比例而不是整数

• ‍max_depth

• • 树的最大深度。

  • 用于控制过拟合，因为更高的深度将让模型学习到非常特定于某个样本的关系

  • 应该使用CV进行调整

• max_leaf_nodes

• • 树中终端节点或叶子的最大数量

  • 可以用于代替max_depth。由于创建了二叉树，因此深度'n'将产生最多2 ^ n个叶子

  • 如果它被定义，则GBM会忽略max_depth

• max_features

• • 搜索最佳拆分时要考虑的特征数量。这些特征将被随机选择。

  • 作为一个经验法则，特征总数的平方根效果很好，但我们可以尝试直到特征总数的30-40％。

  • 较高的值可能导致过度拟合，但通常取决于具体情况。

4.5 XGBoost

XGBoost（extreme Gradient Boosting）是梯度提升算法的高级实现。实践证明，XGBoost是一种高效的ML算法，广泛应用于机器学习竞赛和黑客马拉松。 XGBoost具有很高的预测能力，几乎比其他梯度提升技术快10倍。它还包括各种正规化，可减少过拟合并提高整体性能。因此，它也被称为“正则化提升”技术。

 

让我们看看XGBoost为何比其他技术更好：

 

• 正则化：

• • 标准GBM实现没有像XGBoost那样的正则化

  • 因此，XGBoost还有助于减少过拟合

• 并行处理：

• • XGBoost实现并行处理，并且比GBM更快

  • XGBoost还支持Hadoop上的实现

• 高灵活性：

• • XGBoost允许用户自定义优化目标和评估标准，为模型添加全新维度

• 处理缺失值：

• • XGBoost有一个内置的例程来处理缺失值

• 树剪枝：

• • XGBoost先进行分割，直到指定的max_depth，然后开始向后修剪树并删除没有正向增益的分割

• 内置交叉验证：

• • XGBoost允许用户在提升过程的每次迭代中运行交叉验证，因此很容易在一次运行中获得精确的最佳提升迭代次数

 

示例代码：

 

由于XGBoost会自行处理缺失值，因此你不必再处理。你可以跳过上述代码中缺失值插补的步骤。如下展示了如何应用xgboost：

 

import xgboost as xgb

model=xgb.XGBClassifier(random_state=1,learning_rate=0.01)

model.fit(x_train, y_train)

model.score(x_test,y_test)

0.82702702702702702

回归问题示例代码：

import xgboost as xgb

model=xgb.XGBRegressor()

model.fit(x_train, y_train)

model.score(x_test,y_test)

参数：

 

• nthread

• • 这用于并行处理，应输入系统中的核心数

  • 如果你希望在所有核心上运行，请不要输入此值。该算法将自动检测

• eta

• • 类似于GBM中的学习率

  • 通过缩小每一步的权重，使模型更加健壮

• min_child_weight

• • 定义子节点中所有观察值的最小权重和

  • 用于控制过拟合。较高的值会阻止模型学习关系，这种关系可能高度特定于为某个树所选的具体样本

• max_depth

• • 它用于定义最大深度

  • 更高的深度将让模型学习到非常特定于某个样本的关系

• max_leaf_nodes

• • 树中终端节点或叶子的最大数量

  • 可以用来代替max_depth。由于创建了二叉树，因此深度'n'将产生最多2 ^ n个叶子

  • 如果已定义，则GBM将忽略max_depth

• gamma

• • 仅当产生的分割能给出损失函数的正向减少时，才分割节点。Gamma指定进行分割所需的最小损失减少量。

  • 使算法保守。值可能会根据损失函数而有所不同，因此应进行调整

• subsample

• • 与GBM的子样本相同。表示用于每棵树随机采样的观察值的比例。

  • 较低的值使算法更加保守并防止过拟合，但是太小的值可能导致欠拟合。

• colsample_bytree

• • 它类似于GBM中的max_features

  • 表示要为每个树随机采样的列的比例

 

4.6 Light GBM

在讨论Light GBM如何工作之前，先理解为什么在我们有如此多其他算法时（例如我们上面看到的算法）我们还需要这个算法。当数据集非常大时，Light GBM会击败所有其他算法。与其他算法相比，Light GBM在较大的数据集上运行所需的时间较短。

 

LightGBM是一个梯度提升框架，它使用基于树的算法并遵循逐叶子的方式（leaf-wise），而其他算法以逐层级（level-wise）模式工作。下图帮助你更好地理解二者差异：

逐叶子方式可能在较小的数据集上导致过拟合，但可以通过使用'max_depth'参数来避免这种情况。你可以在本文中阅读有关Light GBM及其与XGB比较的更多信息。

 

示例代码：

import lightgbm as lgb

train_data=lgb.Dataset(x_train,label=y_train)

#define parameters

params = {'learning_rate':0.001}

model= lgb.train(params, train_data, 100)

y_pred=model.predict(x_test)

for i in range(0,185):

   if y_pred[i]>=0.5:

   y_pred[i]=1

else:

   y_pred[i]=0

0.81621621621621621

回归问题示例代码：

import lightgbm as lgb

train_data=lgb.Dataset(x_train,label=y_train)

params = {'learning_rate':0.001}

model= lgb.train(params, train_data, 100)

from sklearn.metrics import mean_squared_error

rmse=mean_squared_error(y_pred,y_test)**0.5

参数：

 

• num_iterations

• • 它定义了要执行的提升迭代次数

• num_leaves

• • 此参数用于设置要在树中形成的叶子数

  • 在Light GBM的情况下，由于拆分是按逐叶子方式而不是深度方式进行的，因此num_leaves必须小于2 ^（max_depth），否则可能导致过拟合

• min_data_in_leaf

• • 非常小的值可能导致过拟合

  • 它也是处理过拟合的最重要的参数之一

• max_depth

• • 它指定树可以生长到的最大深度或级别

  • 此参数的值非常高可能会导致过拟合

• bagging_fraction

• • 它用于指定每次迭代使用的数据比例

  • 此参数通常用于加速训练

• max_bin

• • 定义特征值将被分桶的最大分箱数

  • 较小的max_bin值可以节省大量时间，因为它在离散分箱中存储特征值，这在计算开销上是便宜的

4.7 CatBoost

处理类别型变量是一个繁琐的过程，尤其是你有大量此类变量时。当你的类别变量有很多标签（即它们是高度基数）时，对它们执行one-hot编码会指数级的增加维度，会让数据集的使用变得非常困难。

 

CatBoost可以自动处理类别型变量，并且不需要像其他机器学习算法那样进行大量数据预处理。这篇文章详细解释了CatBoost。

 

示例代码：

 

CatBoost算法有效地处理类别型变量。因此，无需对变量执行one-hot编码。只需加载文件，估算缺失值，就可以了：

from catboost import CatBoostClassifier

model=CatBoostClassifier()

categorical_features_indices = np.where(df.dtypes != np.float)[0]

model.fit(x_train,y_train,cat_features=([ 0,  1, 2, 3, 4, 10]),eval_set=(x_test, y_test))

model.score(x_test,y_test)

0.80540540540540539

回归问题示例代码：

from catboost import CatBoostRegressor

model=CatBoostRegressor()

categorical_features_indices = np.where(df.dtypes != np.float)[0]

model.fit(x_train,y_train,cat_features=([ 0,  1, 2, 3, 4, 10]),eval_set=(x_test, y_test))

model.score(x_test,y_test)

参数：

 

• loss_function

• • 定义用于训练的度量标准

• iterations

• • 可以构建最多多少棵树

  • 树的最终数量可能小于或等于此数字

• learning_rate

• • 定义学习率

  • 用于减少梯度步骤

• border_count

• • 它指定数值型特征的拆分数

  • 它类似于max_bin参数

• depth

• • 定义树的深度   

• random_seed

• • 此参数类似于我们之前看到的'random_state'参数

  • 它是一个整数值，用于定义训练的随机种子

 

现在来到了集成算法这一章节的末尾。我们在这篇文章中已经涵盖了很多内容！

 

结语

集成模型可以指数级地提升模型的性能，有时可以成为第一名和第二名之间的决定因素！在本文中，我们介绍了各种集成学习技术，并了解了这些技术如何应用于机器学习算法。此外，我们在贷款预测数据集上运用了算法。

 

本文为你提供了此主题的扎实理解。如果还有任何建议或问题，请分享在下面的评论部分。此外，我鼓励你实现这些算法，并与我们分享你的结果！

 

原文标题：

A Comprehensive Guide to Ensemble Learning(with Python codes)

原文链接：

https://www.analyticsvidhya.com/blog/2018/06/comprehensive-guide-for-ensemble-models/

译者简介

和中华，留德软件工程硕士。由于对机器学习感兴趣，硕士论文选择了利用遗传算法思想改进传统kmeans。目前在杭州进行大数据相关实践。加入数据派THU希望为IT同行们尽自己一份绵薄之力，也希望结交许多志趣相投的小伙伴。

翻译组招募信息

工作内容：将选取好的外文前沿文章准确地翻译成流畅的中文。如果你是数据科学/统计学/计算机专业的留学生，或在海外从事相关工作，或对自己外语水平有信心的朋友，数据派翻译组欢迎你们加入！

你能得到：提高对于数据科学前沿的认知，提高对外文新闻来源渠道的认知，海外的朋友可以和国内技术应用发展保持联系，数据派团队产学研的背景为志愿者带来好的发展机遇。

其他福利：和来自于名企的数据科学工作者，北大清华以及海外等名校学生共同合作、交流。

点击文末“阅读原文”加入数据派团队~

转载须知

如需转载，请在开篇显著位置注明作者和出处（转自：数据派THU ID：DatapiTHU），并在文章结尾放置数据派醒目二维码。有原创标识文章，请发送【文章名称-待授权公众号名称及ID】至联系邮箱，申请白名单授权并按要求编辑。

发布后请将链接反馈至联系邮箱（见下方）。未经许可的转载以及改编者，我们将依法追究其法律责任。

点击“阅读原文”拥抱组织