Percolation(渗透)问题

Percolation(渗透)问题

@(算法)
Coursera作业链接

直接将马克飞象导出的md文件发到博客，排版不是很清晰，抱歉，可查看GitHub详细代码和文档

---

实际问题：将一个不透水的均质方块分割为N*N，最上方为水源，随机打开方块中任意格子，重复此项操作多次，产生一条路径使水能穿过这个方块到达最下方。

the model

percolation系统使用n-n格点，每个格点site有open/blocked两种状态，如果最上面一行和最底下一行有路径联通，那说明这个系统是percolates的。

---

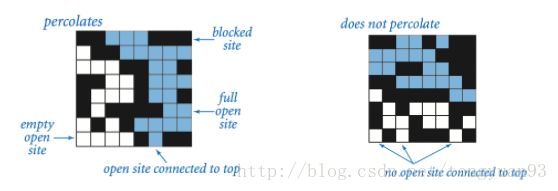
这个问题可以和之前学过dynamic-connectivity问题相联系，因为当open一个site后，这个site需要和周边的open site相连接，这里可以使用quick-find、qucik-union、weighted-quickunion算法。
这个问题看起来比较复杂，实则核心就是进行动态连接。

---

一开始编写代码或者分析的时候思路比较混乱，我使用了二维数组 a[row][col] 来代表这个方形系统，后来直接用一维数组来表达这个方形系统。
类Percolation和使用的WeightedQuickUnionUF算法中均有数组来表达这个方形格点，搞得很混乱。

---

仔细想想，捋清思路，感觉解决算法问题，数据结构的定义和使用需要非常清楚，弄清楚会有事半功倍的效果。

这个实际问题和动态连接区别在于，每个site不仅需要和别的site相连，本身还具备open/block的性质，所以需要单独定义一个数组表示site的open/block性质

之前出现的程序编写之所以不正确，或者思路混乱，是因为数据结构没有理解清楚。本题中的site既要有open&blocked的性质，又得进行Union操作，那本来WeightedQuickUnionUF中只有一组数组用来进行Union，所以我们需要另外定义一组数组来表示Open&blocked性质。同时这两组数组通过下标“对齐”的方式，来展现的就是对一个site进行操作。

我在类Percolation中定义了一个成员~一维数组a用来表示方形系统中每个节点的open/blocked状态，

a[i]=true;//表示site open
a[i]=false;//表示site blocked

定义了一个成员~类WeightedQuickUnionUF对象，这个对象内的数组表示连接情况,
并且下标0表示virtual top site，下标N*N+1表示virtual bottom site.

---

这里简化以3*3方形系统为例：
方形系统：

1	2	3
4	5	6
7	8	9

数组a：

0	1	2
3	4	5
6	7	8

WeightedQuickUnionUF类中的数组：
0表示vitual top site

1	2	3
4	5	6
7	8	9

10表示vitual bottom site
注意：在定义的Percolation类中的方法对site的索引都是通过 (row,col) ，所以涉及到一个数组下标转化问题

例如： (row,col) 来索引方形系统，在数组a中即查看对应site的状态时， a[(row−1)∗N+col−1]
而进行连接时对应 (row,col) 位置的site映射为下标为 (row−1)∗N+col

具体代码：

import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.WeightedQuickUnionUF;
import java.io.FileInputStream;
import java.io.FileNotFoundException;

public class Percolation {
    private WeightedQuickUnionUF weightedQuickUnionUF;
    private boolean[] a;
    private int N;
    private int numberopen;

    public Percolation(int n) {
        N = n;//N*N gird system
        numberopen = 0;//open sites number
        if (n <= 0)
            throw new IllegalArgumentException("n must be a positive number.");
        weightedQuickUnionUF = new WeightedQuickUnionUF(n * n + 2);
        a = new boolean[n * n];
    }

    public boolean isOpen(int row, int col) {
        return a[(row - 1) * N + col - 1] == true;
    }

    public boolean isFull(int row, int col) {//connected to an open site in the top row
        return weightedQuickUnionUF.connected((row - 1) * N + col, 0);
    }

    public int numberOfOpenSites() {
        return numberopen;
    }

    public boolean percolates() {
        return weightedQuickUnionUF.connected(0, N * N + 1);
    }

    public boolean outOfIndices(int row, int col) {
        if ((row > 0 && row <= N) && (col > 0 && col <= N))
            return false;
        return true;
    }

    public void open(int row, int col) {
        if (outOfIndices(row, col))
            throw new IllegalArgumentException("outOfIndices......");
        if (isOpen(row, col))
            return;
        if (row == 1) {//top sites
            weightedQuickUnionUF.union(0, (row - 1) * N + col);
            a[(row - 1) * N + col - 1] = true;
        } else if (row == N) {
            weightedQuickUnionUF.union(N * N + 1, (row - 1) * N + col);
            a[(row - 1) * N + col - 1] = true;
        }
        if (!outOfIndices(row - 1, col) && isOpen(row - 1, col)) {//上site
            weightedQuickUnionUF.union((row - 1) * N + col, (row - 2) * N + col);
            a[(row - 1) * N + col - 1] = true;
        }
        if (!outOfIndices(row + 1, col) && isOpen(row + 1, col)) {//下site
            weightedQuickUnionUF.union(row * N + col, (row - 1) * N + col);
            a[(row - 1) * N + col - 1] = true;
        }
        if (!outOfIndices(row, col - 1) && isOpen(row, col - 1)) {//左site
            weightedQuickUnionUF.union((row - 1) * N + col - 1, (row - 1) * N + col);
            a[(row - 1) * N + col - 1] = true;
        }
        if (!outOfIndices(row, col + 1) && isOpen(row, col + 1)) {//右site
            weightedQuickUnionUF.union((row - 1) * N + col, (row - 1) * N + col + 1);
            a[(row - 1) * N + col - 1] = true;
        }
        if (!outOfIndices(row, col + 1)) {
            a[(row - 1) * N + col - 1] = true;
        }
        numberopen++;
    }

    public static void main(String[] args) {
        try {
            FileInputStream input = new FileInputStream("input50.txt");
            System.setIn(input);
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        }
        int n = StdIn.readInt();
        Percolation percolation = new Percolation(n);
        while (!StdIn.isEmpty()) {
            int i = StdIn.readInt();
            int j = StdIn.readInt();
            percolation.open(i, j);
        }
        System.out.println(percolation.percolates());
        System.out.println(percolation.numberOfOpenSites());
    }
}

带入Coursea-Testing数据验证基本正确的，但存在一个问题，也是共性问题-backwash问题。

---

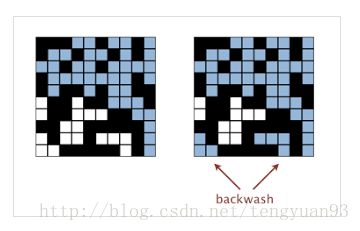
在程序中，每次top/bottom行的site open 后默认连接到vitual top/bottom site，导致最下层的site并没有percolate但是也算在里面了。

---

参考这篇博客，还是只用一个WeightedQuickUnionUF，但新建两个成员数组表示该site是否连接到Top/Bottom，如果某个site既connect top又connect bottom，说明system is connected，然后查看两数组Top/Bottom查看Bottom数组中值为true但在Top数组中值为false的索引，这些索引所对应的site即为backwash部分。