遗传算法求解函数最大值Java实现

我的《自然计算》作业，搬上来。
（原来发布到简书了，现在搬过来）

目录

1. 概述
2. 编码
3. 初始群体的产生
4. 适应度计算
5. 选择运算
6. 交叉运算
7. 变异运算
8. 测试效果
   参考资料

一，概述

本文在理解遗传算法的基本原理的基础上，使用Java语言写了一个小程序来简单实现用遗传算法求解二次函数f(x,y)=x*x+y*y (x和y的取值范围为1到127的正整数)的最大值。完整源码见已上传至我的github，详情请点击此链接：查看本项目全部代码

二，编码

重述一下本文求解的问题：

由于遗传算法的运算对象是表示个体的符号串，所以必须把变量x,y编码为一种符号串。在这里采用无符号二进制整数来表示。因x,y的取值范围为1到127,，则可用两个7位二进制数来分别表示它们。而一个基因就是一个14位二进制串。例如，基因型00000001111111所对应的表现型是：x=0,y=127。在代码中的具体体现为：设计类Chromosome，其具有私有整形字段x,y表示x,y的十进制值、String字段gene表示二进制串。并使用常量定义其最大值或最大长度。代码如下：

public static final int GENG_LENGTH = 14;
public static final int MAX_X = 127;
public static final int MAX_Y = 127;
private int x,y;
private String gene;

三，初始群体的产生

遗传算法是对群体进行的进化操作，所以第一步要产生一个初始种群，再进行后续的交叉、变异、选择等操作。在具体实现上，初始种群的产生较为简单。首先对类Chromosome进行构造函数的编写，主要写了以下两种构造函数：
public Chromosome(String gene) //给定基因串构造染色体
public Chromosome(int x,int y) //给定表现型构造染色体
在这里用到了第二个构造函数，首先随机产生两个1到127之间的数作为X,Y，再调用构造函数生成新染色体并添加到初始种群中去。如此重复，直到种群规模达到要求。具体代码如下:

    public static ArrayList initGroup(int size) {
        ArrayList list = new ArrayList();
        Random random = new Random();
        for(int i = 0; i < size; i++) {
            int x = random.nextInt() % 128;
            int y = random.nextInt() % 128;
            x = x < 0? (-x):x;
            y = y < 0? (-y):y;
            list.add(new Chromosome(x,y));
        }
        return list;
    }

四，适应度计算

遗传算法中以个体适应度评价其优劣程度，其最终目的是选择出适应度较高的个体。本文所求解问题，目标函数总取非负值，并且是以求函数最大值为优化目标，故可直接利用目标函数值作为个体的适应度。具体求解代码如下：

public int calcFitness() {
        return x*x+y*y;
}

五，选择运算

选择运算把当前的群体中适应度较高的个体按照某种规则或模型遗传到下一代个体中。这里我们使用课堂上讲的“轮盘赌”的方式进行选择。“轮盘赌”的思想这里不再赘述，只说一下JAVA代码的具体实现过程。
首先计算种群中每个个体的适应度保存到一个数组里。在这基础上计算“累加适应度”，即第一个适应度为原第一个适应度，第二个为前两个的和，第三个为前三个的和，以此类推。再将此数组每个元素除以总的适应度。然后进行选择，选择次数和设定好的种群规模相同（这样便可以控制种群的规模不会无限的上涨）。每次选择时，先产生一个0到1之间的随机数。在上述数组中遍历找到第一个大于此随机数的元素，这个元素对应的个体被选择。具体代码如下：

public static ArrayList selector(ArrayList fatherGroup,int sonGroupSize) 
{
    ArrayList sonGroup = new ArrayList();
    int totalFitness = 0;
    double[] fitness = new double[fatherGroup.size()];
    for(Chromosome chrom : fatherGroup) {
        totalFitness += chrom.calcFitness();
    }
    int index = 0;
    //计算适应度
    for(Chromosome chrom : fatherGroup) {
        fitness[index] = chrom.calcFitness() / ((double)totalFitness);
        index++;
    }
    //计算累加适应度
    for(int i = 1; i < fitness.length; i++) {
        fitness[i] = fitness[i-1]+fitness[i];
    }
    //轮盘赌选择 
    for(int i = 0; i < sonGroupSize; i++) {
        Random random = new Random();
        double probability = random.nextDouble();
        int choose;
        for(choose = 1; choose < fitness.length - 1; choose++) {
            if(probability < fitness[choose])
                break;
            }
            sonGroup.add(new Chromosome(fatherGroup.get(choose).getGene()));
        }
        return sonGroup;
    }

六，交叉运算

交叉运算是遗传算法中产生新个体的主要操作过程，它以某一概率相互交换某两个个体之间的部分染色体。本文采用单点交叉的方法，具体操作过程是：先对群体进行随机配对；其次随机设置交叉点位置；最后再相互交换配对染色体之间的部分基因。
具体的算法流程按照老师课件上讲的，这里也不赘述了。只说一下具体代码实现原理。这个算法的要点在于随机配对个体进行交叉、字符串的拼接操作和生成新个体。随机配对可以使用一个do while循环，选择两个不同的个体。然后随机选取交叉点，进行两个基因字符串的交叉。最后生成新的个体，采用以下构造函数生成新的个体：public Chromosome(String gene)。
具体代码如下：

public static ArrayList corssover(ArrayList fatherGroup,double probability) {
        ArrayList sonGroup = new ArrayList();
        sonGroup.addAll(fatherGroup);
        Random random = new Random();
        for(int k = 0; k < fatherGroup.size() / 2; k++) {
            if(probability > random.nextDouble()) {
                int i = 0,j = 0;
                do {
                    i = random.nextInt(fatherGroup.size());
                    j = random.nextInt(fatherGroup.size());
                } while(i == j);
                int position = random.nextInt(Chromosome.GENG_LENGTH);
                String parent1 = fatherGroup.get(i).getGene();
                String parent2 = fatherGroup.get(j).getGene();
                String son1 = parent1.substring(0, position) +                                          parent2.substring(position);
                String son2 = parent2.substring(0, position) +                                          parent1.substring(position);
                sonGroup.add(new Chromosome(son1));
                sonGroup.add(new Chromosome(son2));
            }
        }
        return sonGroup;
    }

七，变异运算

变异运算是对个体的某一个或某一些基因按某一较小的概率进行改变，它也是产生新个体的一种操作方法。本文中我们采用如下方式进行变异：遍历群体中所有个体的所有基因位，以一个较小的概率对每个基因位进行变异操作即1变成0,0变成1。在Java代码中具体实现时，我们先编写一个函数对一个个体的基因进行改变，即用新基因串代替旧基因串。该函数编写如下：

public void selfMutation(String newGene) {
        if(newGene.length() != Chromosome.GENG_LENGTH)
            return;
        this.gene = newGene;
        String xStr = newGene.substring(0, Chromosome.GENG_LENGTH/2);
        String yStr = newGene.substring(Chromosome.GENG_LENGTH/2);
        this.x = Integer.parseInt(xStr,2);
        this.y = Integer.parseInt(yStr,2);
}
然后，按照上述说法对每一位基因进行遍历，按指定概率进行变异操作。具体代码如下所示：
public static void mutation(ArrayList fatherGroup,double probability) {
        Random random = new Random();
        Chromosome bestOne = Chromosome.best(fatherGroup);
        fatherGroup.add(new Chromosome(bestOne.getGene()));
        for(Chromosome c : fatherGroup) {
            String newGene = c.getGene();
            for(int i = 0; i < newGene.length();i++){
                if(probability > random.nextDouble()) {
                    String newChar = newGene.charAt(i) == '0'?"1":"0";
                    newGene = newGene.substring(0, i) + newChar +                                   newGene.substring(i+1);
                }
            }
            c.selfMutation(newGene);
        }
}

八，测试效果

以上实现了所有子模块。下面使用上述模块进行实际的遗传算法求解操作。首先产生初始种群，按照交叉、变异、选择的顺序进行循环，直到选出符合要求的个体，这里设置的条件为适应度大于等于32258时终止，这也是本题中能达到的最大适应度。

final int GROUP_SIZE = 20;//种群规模
final double CORSSOVER_P = 0.6;//交叉概率
final double MUTATION_P = 0.01;//变异概率
ArrayList group =                                               Chromosome.initGroup(GROUP_SIZE);
Chromosome theBest;
do{
    group = Chromosome.corssover(group, CORSSOVER_P);
    Chromosome.mutation(group, MUTATION_P);
    group = Chromosome.selector(group, GROUP_SIZE);
    theBest = Chromosome.best(group);
    System.out.println(theBest.calcFitness());
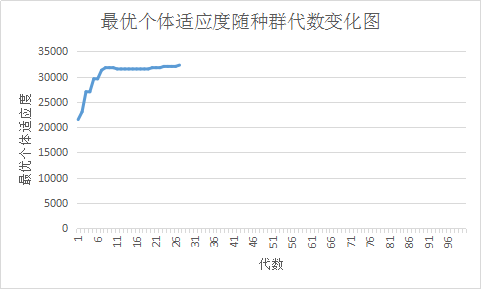
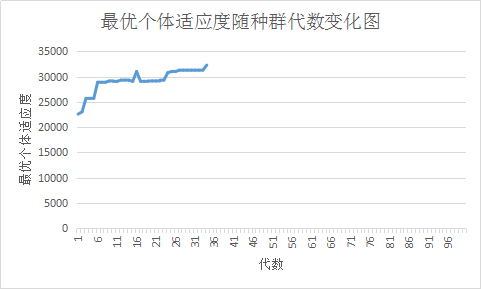
}while(theBest.calcFitness() < 32258);

如上述代码所示，在每次迭代后输出当前种群中的最优个体。下面进行了三次测试。最优个体适应度随种群代数变化图，如下图所示（三次的结果）。可以看出随着迭代次数的增加，种群中的最优个体适应度总体呈上升趋势，最终一般在50代之内就会找到满足要求的个体。

参考资料：

[1]遗传算法的例子 http://blog.csdn.net/b2b160/article/details/4680853/
[2]老师的课件 cn01-IntroGA-v1.00.ppt