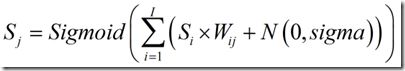这篇写的主要是翻译网上一篇关于受限玻尔兹曼机的tutorial,看了那篇博文之后感觉算法方面讲的很清楚,自己收获很大,这里写下来作为学习之用。
原文网址为:http://imonad.com/rbm/restricted-boltzmann-machine/
翻译如下:
(注:下文中的“我”均指原作者)
受限玻尔兹曼机——简单的教程
我读过很多关于RBM的论文,但是要理解它所有的实现细节似乎有些难度。
因此我想和大家分享一些我在面对这些困难时收获的经验。我的教程是基于RBM的一个变种,被称为连续受限玻尔兹曼机(continuous restricted Boltzmann machine),可以简写为CRBM。CRBM的实现和以(0,1)二元值作为可能的激活值的原始的RBM的实现过程十分接近。
在文章末尾我提供了一些用Python写的代码。但并不能保证所提供的实现完全正确,因此如果发现有bug,请告知。
首先你可以看一下关于描述RBM神经网络理论的原始的论文:
RBM application to Netflix challenge
Boltzmann Machine – Scholarpedia
Continuous RBM
(这些链接均可以下载对应的pdf)
什么是受限玻尔兹曼机
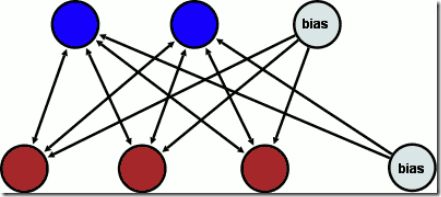
受限玻尔兹曼机是一个随机神经网络(即当网络的神经元节点被激活时会有随机行为,随机取值)。它包含一层可视层(visible layer)和一层隐含层(hidden layer)。在同一层的神经元之间不会相互连接,而不在同一层的神经元之间会相互连接(如图1所示)。神经元之间的连接是双向的以及对称的。这意味着在网络进行训练以及使用时信息会在两个方向上流动,而且两个方向上的权值是相同的。
图1 受限玻尔兹曼机
RBM网络以如下方式工作:
首先用一定的数据集来训练网络,设置可视层神经元的值匹配数据集中数据点的值。
当网络训练完成之后,我们可以用它来对未知数据进行计算从而进行分类(这就是所谓的非监督学习)。
数据集
作为教程的示范,我将人工生成数据集。这些数据集是2D的,将构成图2中的模式。我会选择用500组数据点进行训练。因为每个数据点的取值都是在0到1之间,因此这里将会用连续的受限玻尔兹曼机。我试过很多的2D模式,这个对与CRBM来说要相对难训练一些。
图2 训练样本
训练算法
用于训练RBM的算法被称作contrastive divergence learning(姑且称为对比发散训练)。
(关于这个算法可以参考下面的链接)
More info on Contrastive Divergence
令W为一个IxJ的矩阵(I是可视层神经元的个数,J是隐含层神经元的个数)代表神经元之间连接的权重。
每个神经元的输入值都是通过其他层与其相连的神经元计算而来的。
当前神经元的状态S通过权重和每个输入相乘而来,并进行求和,然后将所得的和作为非线性的sigmoidal函数的参数进行计算:
这里Si是给定层的状态加上一个被设为恒为1的神经元偏置
N(0,sigma)是一个服从正态分布的随机数,平均值为0.0,标准差为sigma(我设定的sigma=0.2)。
在我的例子中非线性函数为:
其中lo和hi是输入值的下界和上界(在我的例子中分别为0,1),因此可以写为:
A是在训练过程中确定的一个参数。
contrastive divergence是计算出的一个值(实际上是一个矩阵),并且它用来调节权重的值。通过改变W的增量来训练W的值。
令W0是权重的初始矩阵,开始被设定为很小的随机数值。我用N(0,0.1)来完成这一步。
令CD=
那么对W进行一次更新的值为W":
W" = W + alpha*CD
这里的alpha是学习速率。这里有许多复杂的方法来更新W,比如用到“动量”或者“代价函数”,来避免W的值波动过大。
Contrastive Divergence的解释
(我感觉这里写的比较清楚,对我启发比较大)
对Contrastive Divergence究竟是什么以及如何实现它还存在很多的困惑。
我也花了很多时间来理解它。
首先CD是一个大小为IxJ的矩阵。因此必须要计算I和J的每一个组合。
<...>是用来计算数据集中每个数据点的平均值的操作。
Si.Sj是当前激活的神经元I和神经元J的乘积(当然是这样的:))。其中Si是可视层神经元的状态,Sj是隐含层神经元的状态。
<...>的下标意味着进行0次或者N次重构步骤之后的平均值。
图3 训练受限玻尔兹曼机
那么重构的过程是如何进行的呢?
1. 从数据集中取一个数据点。
2. 用这个点来设置可视层神经元的状态为Si。
3. 根据上面的方程式和可视层神经元的状态来计算隐含层神经元的状态。
4. 现在Si和Sj的值可以用来计算(Si.Sj)0,这里(...)只是意味着值而不是求平均。
5. 以步骤3中的方式用隐含层的状态Sj来计算可视层的状态Si,这就是所谓的重构。
6. 通过从步骤5中计算出来的可视层的Si来计算隐含层的状态Sj。
7. 现在可以用Si和Sj来计算(Si.Sj)1,如图3所示。
8. 多次重复步骤5,6和7来计算(Si.Sj)n,其中n是一个比较小的数,可以将其随训练步骤增加而获得更好的精度。
整个算法可以概括为:
# 对于每一次训练:
# 对数据集中每个训练样本:
# 令CDpos = 0, CDneg = 0 (这两个都是矩阵)
# 执行步骤1~8
# 累加 CDpos = CDpos + (Si.Sj)0
# 累加 CDneg = CDneg + (Si.Sj)n
# 通过除以数据样本的个数来计算CDpos和CDneg的平均值
# 计算 CD =
# 更新权值和偏置值W" = W + alpha*CD (偏置值总是为1.0,不变)
# 计算某个"误差函数",比如步骤1和步骤5的Si的平方误差和,也就是数据和重构之间的误差。
# 重复这个训练过程直到误差小于某个设定的值或者完成了给定次数的训练。
对于可视化层,A的值是固定不变的,而对于隐含层而言,同样需要利用CD矩阵来调节A的值的大小,但是不是依据之前的方程式,
而是利用:
CD = (
在我的代码中我在最开始设置n=20,并逐渐增大到50。
在大多数的计算步骤中,算法可以通过简单的矩阵乘法计算。
RBM的使用
在RBM的训练过程结束之后,可以展示出它对新样本预测的性能如何。
我是用500个样本的训练数据,这些数据随机均匀分布在2D区间(0..1,0..1)之间。
可视层神经元的状态用每个数据点的值来设定,并且步骤1)2)3)5)被重复多次。
重复的次数是在训练过程中n的最大值。
在第n次计算结束时,可视层神经元的状态则代表数据的重构。对于每个数据点都是这样重复的。
所有重构出来的点形成了一个2D图像模式,可以和最开始的图片进行比较。
CRBM的Python实现
在文章的最后我提供了用Python实现的连续受限玻尔兹曼机。其中大多数的计算都是用的NumPy库进行的。我利用PyLab和SciPy来进行一些可视化。在图4中展示了这些图片,并用高斯内核插值以便可以观察出这些原始点和重构点的密度。
图4 训练数据和重构数据
下一幅图展示了初始点和重构点。初始点用蓝色标出,重构点用红色表示,并且用绿色的线来连接初始点和重构点。
图5 训练数据(蓝色)和重构数据(红色)
我注意到主要的困难是参数的调节。
我是用下面的参数,如果有更好的参数请让我知道。
sigma=0.2
A=0.1(在可视层)
Learning Rate W = 0.5
Learning Rate A = 0.5
Learning Cost = 0.00001
Learning Moment = 0.9
RBM的结构是2个可视层节点和8个隐含层节点。在某些试验中用4个神经元的简单模型有时候也足够成功重构数据。
Python code for Restricted Boltzmann Machine
源代码如下:
"""
Continuous Restricted Boltzmann Machine
14/09/2008 - v. 0.1 by http://imonad.com
"""
from numpy import *
from numpy.random import *
import pylab as p
from scipy import stats, mgrid, c_, reshape, random, rot90
import psyco
psyco.full()
class RBM:
def __init__(self, nvis, nhid):
self.sig = 0.2
self.epsW = 0.5
self.epsA = 0.5
self.nvis = nvis
self.nhid = nhid
self.Ndat = 500
self.cost = 0.00001
self.moment = 0.90
self.Svis0 = zeros( nvis+1, dtype=float32)
self.Svis0[-1] = 1.0
self.Svis = zeros( nvis+1, dtype=float32)
self.Svis[-1] = 1.0
self.Shid = zeros( nhid+1, dtype=float32)
self.W = standard_normal((nvis+1, nhid+1))/10
self.dW = standard_normal((nvis+1, nhid+1))/1000
self.Avis = 0.1*ones( nvis+1, dtype=float32)
self.Ahid = ones( nhid+1, dtype=float32)
self.dA = zeros( nvis+1, dtype=float32)
self.dat = self.genData()
def genData(self):
c1 = 0.5
r1 = 0.4
r2 = 0.3
# generate enough data to filter
N = 20* self.Ndat
X = array(random_sample(N))
Y = array(random_sample(N))
X1 = X[(X-c1)*(X-c1) + (Y-c1)*(Y-c1) < r1*r1]
Y1 = Y[(X-c1)*(X-c1) + (Y-c1)*(Y-c1) < r1*r1]
X2 = X1[(X1-c1)*(X1-c1) + (Y1-c1)*(Y1-c1) > r2*r2]
Y2 = Y1[(X1-c1)*(X1-c1) + (Y1-c1)*(Y1-c1) > r2*r2]
X3 = X2[ abs(X2-Y2)>0.05 ]
Y3 = Y2[ abs(X2-Y2)>0.05 ]
#X3 = X2[ X2-Y2>0.15 ]
#Y3 = Y2[ X2-Y2>0.15]
X4=zeros( self.Ndat, dtype=float32)
Y4=zeros( self.Ndat, dtype=float32)
for i in xrange(self.Ndat):
if (X3[i]-Y3[i]) >0.05:
X4[i] = X3[i] + 0.08
Y4[i] = Y3[i] + 0.18
else:
X4[i] = X3[i] - 0.08
Y4[i] = Y3[i] - 0.18
print "X", size(X3[0:self.Ndat]), "Y", size(Y3)
return(vstack((X4[0:self.Ndat],Y4[0:self.Ndat])))
# Sigmoidal Function
def sigFun(self, X, A):
lo = 0.0
hi = 1.0
return(lo + (hi-lo)/(1.0 + exp(-A*X)))
# visible=0, hidden=1
def activ(self, who):
if(who==0):
self.Svis = dot(self.W, self.Shid) + self.sig*standard_normal(self.nvis+1)
self.Svis = self.sigFun(self.Svis, self.Avis)
self.Svis[-1] = 1.0 # bias
if(who==1):
self.Shid = dot(self.Svis, self.W) + self.sig*standard_normal(self.nhid+1)
self.Shid = self.sigFun(self.Shid, self.Ahid)
self.Shid[-1] = 1.0 # bias
def wview(self):
import pylab as p
p.plot(xrange(size(self.W[2])),self.W[2], 'bo')
p.show()
def learn(self, epochmax):
Err = zeros( epochmax, dtype=float32)
E = zeros( epochmax, dtype=float32)
self.stat = zeros( epochmax, dtype=float32)
self.stat2 = zeros( epochmax, dtype=float32)
ksteps = 1
for epoch in range(1,epochmax):
wpos = zeros( (self.nvis+1, self.nhid+1), dtype=float32)
wneg = zeros( (self.nvis+1, self.nhid+1), dtype=float32)
apos = zeros( self.nhid+1, dtype=float32)
aneg = zeros( self.nhid+1, dtype=float32)
if(epoch>0):
ksteps=50
if(epoch>1000):
ksteps=(epoch-epoch%100)/100+40
self.ksteps = ksteps
for point in xrange(self.Ndat):
#print(self.dat[:][point])
self.Svis0[0:2] = self.dat[:,point]
self.Svis = self.Svis0
# positive phase
self.activ(1)
wpos = wpos + outer(self.Svis, self.Shid)
apos = apos + self.Shid*self.Shid
# negative phase
self.activ(0)
self.activ(1)
for recstep in xrange(ksteps):
self.activ(0)
self.activ(1)
tmp = outer(self.Svis, self.Shid)
wneg = wneg + tmp
aneg = aneg + self.Shid*self.Shid
delta = self.Svis0[0:2]-self.Svis[0:2]
# statistics
Err[epoch] = Err[epoch] + sum(delta*delta)
E[epoch] =E[epoch] -sum( dot(self.W.T, tmp) )
self.dW = self.dW*self.moment + self.epsW * ((wpos-wneg)/size(self.dat) - self.cost*self.W)
self.W = self.W + self.dW
self.Ahid = self.Ahid + self.epsA*(apos-aneg)/(size(self.dat)*self.Ahid*self.Ahid)
Err[epoch] = Err[epoch]/(self.nvis*size(self.dat))
E[epoch] = E[epoch]/size(self.dat)
if (epoch%100==0) or (epoch==epochmax) or (epoch==1):
print "epoch:", epoch, "err:", round_(Err[epoch], 6), "ksteps:", ksteps
self.stat[epoch] = self.W[0,0]
self.stat2[epoch] = self.Ahid[0]
self.Err = Err
self.E = E
def reconstruct(self, Npoint, Nsteps):
X = array(random_sample(Npoint))
Y = array(random_sample(Npoint))
datnew = vstack((X, Y))
self.datout = zeros( (2,Npoint), dtype=float32)
for point in xrange(Npoint):
self.Svis[0:2] = datnew[:,point]
for recstep in xrange(Nsteps):
self.activ(1)
self.activ(0)
self.datout[:,point] = self.Svis[0:2]
def contour(self, p, dat):
X, Y = mgrid[0.0:1.0:100j, 0.0:1.0:100j]
positions = c_[X.ravel(), Y.ravel()]
val = c_[dat[0,:], dat[1,:]]
kernel = stats.kde.gaussian_kde(val.T)
Z = reshape(kernel(positions.T).T, X.T.shape)
p.imshow( rot90(Z) , cmap=p.cm.YlGnBu, extent=[0, 1, 0, 1])
p.plot(dat[0,:], dat[1,:], 'r.')
p.axis([0.0, 1.0, 0.0, 1.0])
if __name__ == "__main__":
seed(12345)
rbm = RBM(2,8)
rbm.learn(4000)
kkk=0
p.figure(1)
p.plot(xrange(size(rbm.E)),rbm.E, 'b+')
p.figure(2)
p.plot(xrange(size(rbm.Err)),rbm.Err, 'r.')
p.figure(3)
if kkk==1:
p.plot(rbm.dat[0,:],rbm.dat[1,:], 'bo')
p.axis([0.0, 1.0, 0.0, 1.0])
else:
rbm.contour(p, rbm.dat)
p.savefig("dat.png",dpi=100)
rbm.reconstruct(rbm.Ndat, 1)
p.figure(4)
if kkk==1:
p.plot(rbm.datout[0,:],rbm.datout[1,:], 'b.')
p.axis([0.0, 1.0, 0.0, 1.0])
else:
rbm.contour(p, rbm.datout)
rbm.reconstruct(rbm.Ndat, 20)
p.figure(5)
if kkk==1:
p.plot(rbm.datout[0,:],rbm.datout[1,:], 'b.')
p.axis([0.0, 1.0, 0.0, 1.0])
else:
rbm.contour(p, rbm.datout)
rbm.reconstruct(rbm.Ndat, rbm.ksteps)
p.figure(6)
if kkk==1:
p.plot(rbm.datout[0,:],rbm.datout[1,:], 'b.')
p.axis([0.0, 1.0, 0.0, 1.0])
else:
rbm.contour(p, rbm.datout)
p.savefig("reconstruct.png",dpi=100)
p.figure(7)
p.plot(xrange(size(rbm.stat)), rbm.stat, "b.")
p.figure(8)
p.plot(xrange(size(rbm.stat2)), rbm.stat2, "b.")
print(around(rbm.W,5))
print(rbm.Ahid)
p.show()