曾被无视多年,却成就19世纪最伟大的一场革命,影响了整个世界!
本文经授权转载自微信公众号:超级数学建模(ID:supermodeling)
本音频由邢台第十五中学苑老师录制
一起探讨数学背后充满智慧的传奇故事
推荐阅读《最后的数学问题》
几个世纪以来,人们对欧几里得几何第五公理的质疑不绝于耳,不断有人试图从其他9 条公理出发证明第五公理,甚至还有人尝试用一条更清晰、简洁的假设来代替它。
当然,这些努力都没有成功,而另一些几何学家试图回答一个令人困惑的猜想:“如果它 是假的呢?”这些尝试开始激起人们心中的疑惑,甚至有人怀疑,欧几里得的公理到底真的是不证自明的,还只是基于经验的。
最终,令人震惊的结论在19 世纪出现了:数学家发现,人们选择另一条不同于欧几里得第五公理的公理,就可以建立一门全新的几何学。
而且,那些“非欧”几何学能像欧几里得几何学那样从原理上准确地描述物理空间。
让我们在这里暂停一下,先把“选择”这个词搞清楚。几千年来,欧几里得几何一直被视为独一无二的,而且是必然如此的—— 它被认为是对空间唯一正确的描述。
然而,人们现在可以选择公理并得到同样正确的描述,这一事实让大家对整个概念体系产生了浓厚兴趣。仔细构建的推理体系似乎在一夜之间变成了一场游戏,在这场游戏中,公理不过是扮演了规则的角色。你可以改变公理来玩一场完全不同的游戏。
不过,这种认知给理解数学本质带来的巨大冲击,超乎了人们的想象。许多富有想象力和创造力的数学家,为了给欧几里得几何最后的一击铺平了道路。
其中值得特别关注的有基督教神父吉罗拉莫·萨凯里,他深入研究了,如何用另一种不同形式的表述来代替第五公理;德国数学家乔治·克鲁格,和约翰·海因里希·朗伯,这两人第一次意识到:欧几里得几何可能会被其他几何体系替代。
约翰·海因里希·朗伯
除此之外,一些数学家为“欧几里得几何是唯一一种宇宙空间表现形式”,这一思想的葬身之棺钉下了最后一颗钉子。
而这一荣誉应当由三位数学家来分享,他们一位来自俄罗斯,一位来自匈牙利,还有一位来自德国。
第一位公开发表论文,从整体上阐述这门全新几何学的人,就是俄罗斯数学家:尼古拉·伊万诺维奇·罗巴切夫斯基。
尼古拉·伊万诺维奇·罗巴切夫斯基
这是一种建立在像马鞍一样的弯曲表面上的几何。在这门几何学中(今天我们称为双曲几何),替代欧几里得第五公理的表述就成了如下的形式:
“在平面上给定一条直线和不在直线上的一点,经过该点至少能作出两条与给定直线平行的平行线。”
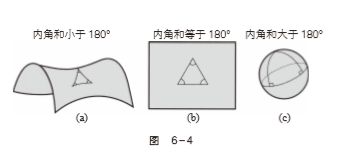
罗巴切夫斯基几何学与欧几里得几何学还有一个重要的区别:在欧几里得几何中,三角形的内角和总是180°(图 6-4b),而在罗巴 切夫斯基几何中,三角形的内角和总是小于180°(图 6-4a)。
罗巴切夫斯基的学术观点主要发表在《喀山公报》上,而这份杂志在当时并不出名,所以他的理论完全没有得到应有的重视。
而在此之前,匈牙利年轻的数学家鲍约·亚诺什并未看到罗巴切夫斯基的文章,也在1820 年左右,系统地阐述了与罗巴切夫斯基几何类似的几何学理论。
出于年轻人特有的激情,他在1823 年给父亲的信中写道:
“我发现了一些精美绝伦的东西,这让我无比震惊……我从一片虚无中创造了一个全新的世界。”
他的父亲鲍约·法卡斯也是一名数学家,在1825年,亚诺什已经完成了研究,准备让父亲看看自己关于这门新几何学的理论著作的草稿。
虽然年轻的亚诺什兴高采烈,但他的父亲却不能确定这种理论是否正确。不过,法卡斯还是决定把儿子的新几何,作为他本人的两卷本著作的附录一同出版——法卡斯的书以研究经典几何、代数和分析学的基础为主要内容。
鲍约·法卡斯
据说,这本书写作手法十分有趣,书名就叫《为好学的年轻人所写的关于数学基本原理的随笔》。
该书出版后,法卡斯送给了一本给他的朋友高斯,而高斯不仅在当时就被认为是最杰出的数学家,并且被后世许多人推崇为,人类有史以来最伟大的数学家之一,足以和阿基米德与牛顿并肩。
高斯在1832 年 3 月 6 日给法卡斯回了信。不过,他的评论与年轻的亚诺什所期望的并不完全一样。
“如果我一上来就说,我无法称赞这本著作,您也许会感到十 分惊讶。但除此之外,我的确没法再说别的了。这是因为如果我表扬它,就是在表扬我自己。
事实上,这本书的所有内容——您儿子的思想和他所得出的结论——与我的想法几乎一模一样。而在过去 的 30 或 35 年里,这些想法一直占据着我的一部分思考。所以我有些茫然无措。迄今为止,我从未把这些结论写下来,而且我当时想,在我的有生之年都不会把它们拿出来发表。”
虽然法卡斯觉得高斯对亚诺什的评价很高,他认为高斯的赞扬 “令人欣喜”,但是,亚诺什却因为自己的研究与高斯的思想完全相同而备受打击,并从此之后彻底地消沉了。
高斯
毋庸置疑,高斯的确对非欧几何进行了大量思考。
他在1799 年 9 月的一篇日记中写道:“在几何的原理方面,我们取得了非凡的成就。”接着,他在1813 年又提到:“关于平行线理论, 我们如今并不比欧几里得知道得更多。这是数学中让人脸红的一部分,它迟早会变成另一种完全不同的形式。”
几年之后,高斯在 1817 年 4 月 28 日所写的一封信中又讲道:“我现在越来越确信,今 天的(欧几里得)几何学的必然性并不能被证实。”
最终,高斯得出的结论:欧几里得几何不能被视为普适的永恒真理,并且“不能把欧几里得几何与算术相提并论(因为算术是先验性的),但大致可以与力学相提并论”。
费尔迪南德·施韦卡特是一位法理学教授,他在1818 年或1819 年写信告诉高斯,他也独立得出了类似的结论。
由于高斯和施韦卡特都没有公开发表过他们的观点和结论,所以在传统上,人们一直把发现非欧几何的荣誉,归于罗巴切夫斯基和鲍约·亚诺什——其实,这两位绝不是非欧几何的独家“缔造者。
双曲几何犹如晴天霹雳一般,打破了数学世界的沉寂,给欧几里得几何学唯一的不可动摇的空间描述,带来了沉重打击。在高斯、罗巴切夫斯基和鲍约之前,欧几里得几何长期以来一直被视为世界的本质。
然而,人类还可以选择一套不同的公理,来构建一门完全不同的几何。这一事实让人们第一次开始怀疑,数学似乎是人类的发明,而不是独立存在于人思维之外、等待人类去发现的真理。
同时,欧几里得几何学与真实物理空间之间的直接关系也破裂了。 “数学是宇宙的语言”这一思想暴露出了致命的缺陷。
当高斯的一名学生波恩哈德·黎曼,证明双曲几何并不是非欧几何的唯一形式时,欧几里得几何学的优越地位变得更加岌岌可危了。
黎曼于1854 年6月10日在德国哥廷根做了一场演讲,演讲中处处闪耀着天才的思想火花。
上图是后来公开发表的演讲稿的第一页
黎曼借助“以几何基础为前提的猜想”表达了 自己的观点。
黎曼一开始就说:“几何学预先假设了空间的概念,并假定了构建空间的基本原理。但是,几何对此仅给出了名称上的定义,而这些概念和原理的本质说明是以公理的形式出现的。”
但他接着又指出:“那些预先假设之间的关系还不为人所知。我们看不出它们之间的任何联系是否是必然的,或者在多大程度上是必然的,甚至不能预先确定,它们之间是否可能存在联系。”
在各种可能的几何学理论中,黎曼重点研究了椭圆面几何。这是一门建立在椭圆体表面上的几何理论(上图6-4c)。
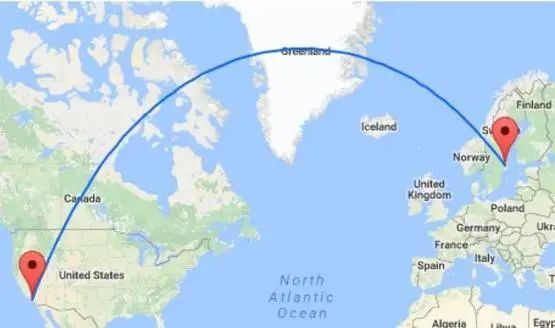
请注意,在这门几何学中,两点之间的最短距离并不是一条线段,而是大圆上的一段弧, 而这个圆的圆心恰好也是球心。
航空公司就是利用这一特性来确定飞行航线的,所以,从美国到欧洲的国际航班的飞行线路并不是我们在地图上看到的直线,而是一段向北的大圆弧。
你可以很轻易地证明,任意这样的两段大圆弧都会在直径的两端相交。例如,地球上的任意两条经线,在赤道附近看上去是平行的,实际上却会在两极相交。
在欧几里得几何学中,经过直线外的一点只能作一条与该直线平行的平行线。
非欧几何则不同,在双曲几何中,经过直线外的一点至少能作两条与该直线平行的平行线。
而在椭圆面几何中,连一条这样的平行线也没有。
黎曼把非欧几何的概念推向了更为广泛的天地——他把这类几何引入三维、四维,甚至维度更高的空间曲面中。
最终,欧几里得几何学对空间的感知竟然被证明是后天学来的,而不是直觉获取的。
面对这些剧烈的变化,法国著名的数学家亨利·庞加莱提出,几何的公理 “既不是综合的先验性直觉,也不是经验事实。它们是约定俗成的。我们根据经验事实做出选择,而这种选择是自由的”。
亨利·庞加莱
换句话说, 庞加莱仅把公理视为“伪装的定义”。庞加莱的观点不仅受到了上述非欧几何思想的启发,同时也受到了当时不断涌现的其他新几何的鼓舞。
很快,对欧几里得几何缺点的深刻认识引起了数学家对数学基础的普遍关注,特别是数学与逻辑之间的关系。我在这里提一句:“公理是不证自明的”这一观点已经动摇了。
虽然19 世纪的人们也见证了代数和分析领域的一些重大进展,但是,几何学的发展对数学本质问题的影响是最深远的。
以上内容,节选自著名科学家马里奥·利维奥的《最后的数学问题》。
毫无疑问,数学是复杂且重要的,毕竟现代科学发展的基石就是数学。然而时至今日,对于数学究竟是什么,这样一个看似简单的问题,我们仍然无法回答。
从信奉“万物皆数”的毕达哥拉斯,到剔除“我思,故我在”的笛卡尔,再到反对柏拉图主义的阿蒂亚,在这本书中,利维奥通过对千百年来不断演变的数学思想,以及数学家的传奇人生进行梳理,尝试着为我们澄清数学的本质。
那到底什么才是数学的本质?它是人类的发明还是发现?我们常说数学能解释宇宙万物,但这种威力究竟从何而来?
点击下方链接,让我们一起看看,科学家利维奥的讲解。
豆瓣评分 8.6
畅销世界的数学哲学史经典著作
《最后的数学问题》
[美] 马里奥·利维奥 著
黄征 译
本书讲述了数学概念的演化过程,引经据典地从哲学、历史、文化角度全方位地探讨了数学的本质,揭示了数学与物质世界、与人类思维之间的微妙关系,讨论了困惑几代思想家的重大问题,讲述了数学、哲学和物理学巨匠们的生活经历与思想,是一本妙趣横生而又十分经典的数学思想史著作。
本文作者:超模君,超级数学建模公众号主编,数学与交叉科学教育自媒体博主。爱分享有用的数学建模知识,爱深挖有趣的交叉科学人物故事,爱为靠谱的现代教育产品打call。著有《芥子须弥·大科学家的小故事》,由清华大学出版社2019年出版。
关注我
为数学与交叉科学教育崛起点赞!
☟ 一键拥有