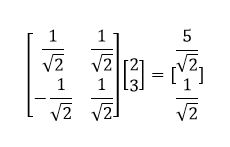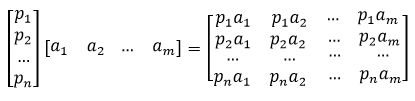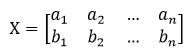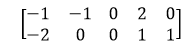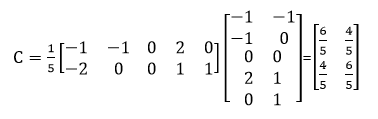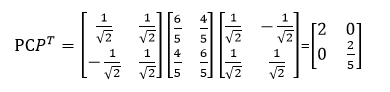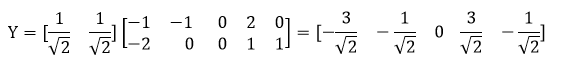图像降维(一)
Principal Component Analysis(PCA)
通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降维。
数学知识:
1、内积
已知两个向量![]() ,则内积
,则内积![]() ,可以看作向量
,可以看作向量![]() 在向量
在向量![]() 的投影值。
的投影值。
2、基
若有一个向量(2,3),通常是指这个向量在x轴方向投影为2,在y轴方向投影为3.
更正式的说,向量(x,y)表示线性组合
其中的(1,0)和(0,1)称为基。
因此我们描述一组向量的第一步就是确定一组基,然后再计算向量在这组基上的投影值。任何一组线性无关的向量均可以作为一组基。例如,我们将(1,1)和(-1,1)作为基,一般来说,我们希望基的模为1,因此我们将其单位化:![]()
那么(2,3)在![]() 上的投影可以用内积来计算得到
上的投影可以用内积来计算得到![]() .注意,上述基是正交向量,但是线性无关不代表一定是正交。
.注意,上述基是正交向量,但是线性无关不代表一定是正交。
同时,我们发现:
基变换可以变为矩阵相乘。矩阵类似于线性变换。
推广一下:如果我们有M个N维向量,想将其变换为由R个N维向量表示的新空间中,那么首先将R个基按行组成矩阵A,然后将向量按列组成矩阵B,那么两矩阵的乘积AB就是变换结果,其中AB的第m列为A中第m列变换后的结果。
3、降维
若基向量的个数(k)小于向量本身维数(N),则是达到了降维的效果。不同的基对于数据有着不同的表示,那么我们应该如何选择最优基。
3.1方差
我们希望数据与数据之间的差异性尽量大,才能便于分类,即是希望投影值尽量分散。在数学中方差可以表示数据的分散程度。
u表示数据的均值,为了计算方便,我们一般先处理数据,使其均值为0.
问题转化为:寻找一个一维基,使得所有数据变换为这个基上的坐标表示后,方差值最大。
3.2协方差
对于二维数据降维到一维数据,按照上面的方法找到方差值最大就行。但是对于高维数据来说,仅此一个条件并不能完全决定。三维数据降维到二维时,首先我们希望找到一个方向使得投影后方差最大,这样就完成了第一个方向的选择,继而我们选择第二个投影方向。
如果我们还是单纯只选择方差最大的方向,很明显,这个方向与第一个方向应该是“几乎重合在一起”,显然这样的维度是没有用的,因此,应该有其他约束条件。从直观上说,让两个字段尽可能表示更多的原始信息,我们是不希望它们之间存在(线性)相关性的,因为相关性意味着两个字段不是完全独立,必然存在重复表示的信息。数学上协方差表示两组数据的相关性:
当协方差为0时,表示两个字段完全独立。为了让协方差为0,我们选择第二个基时只能在与第一个基正交的方向上选择。因此最终选择的两个方向一定是正交的。
至此,我们得到了降维问题的优化目标:将一组N维向量降为K维(K大于0,小于N),其目标是选择K个单位(模为1)正交基,使得原始数据变换到这组基上后,各字段两两间协方差为0,而字段的方差则尽可能大(在正交的约束下,取最大的K个方差)。
3.3协方差矩阵
假设有一个矩阵:
然后我们用X乘以X的转置,并乘上系数1/m:
这个矩阵对角线上的两个元素分别是两个字段的方差,而其它元素是a和b的协方差。两者被统一到了一个矩阵的。根据矩阵相乘的运算法则,这个结论很容易被推广到一般情况:
设我们有m个n维数据记录,将其按列排成n乘m的矩阵X,设C=1mXXT,则C是一个对称矩阵,其对角线分别个各个字段的方差,而第i行j列和j行i列元素相同,表示i和j两个字段的协方差。
3.4协方差矩阵对角化
PCA算法步骤:
设有m条n维数据。
1)将原始数据按列组成n行m列矩阵X
2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3)求出协方差矩阵 ![]()
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6)Y=PX即为降维到k维后的数据
实例:
对其进行0均值化处理:
求协方差矩阵:
求解后特征值为:
对特征值分解后按照特征值大小排序,取前多少个。通过特征值排列 ,我们可以得到数据在这些特征向量上的分布和多样性。
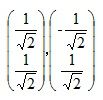
其对应的特征向量分别是:
其中对应的特征向量分别是一个通解,c1和c2可取任意实数。那么标准化后的特征向量为:
因此我们的矩阵P是:
可以验证协方差矩阵C的对角化:
最后我们用P的第一行乘以数据矩阵,就得到了降维后的表示: