决策树学习 -- ID3算法和C4.5算法(C++实现)
前言
在学习西瓜书的时候,由于书本讲的大多是概念,所以打算用C++实现它的算法部分(至于python和matlab实现,实现简单了很多,可以自己基于C++代码实现)。至于测试数据,采用了书中关于西瓜的数据集。
什么是决策树
首先,决策树(也叫做分类树或回归树)是一个十分常用的分类方法,在机器学习中它属于监督学习的范畴。由于决策树是基于树结构来决策的,所以学习过数据结构的人,相对来说会比较好理解。
一般的,一颗决策树包含一个根结点,若干个内部结点和若干个叶结点;叶子结点对应于决策结果,其他每个结点则对应一个属性测试;每个结点包含的样本集合根据属性测试的结果被划分到子结点中;根节点包含样本全集。从根结点到每个叶结点的路径对应了一个判定测试序列。决策树学习的目的是为了产生一颗泛化能力强,即处理未见示例能力强的决策树,其基本流程遵循简单且直观的“分而治之”策略。(《机器学习(周志华)》)
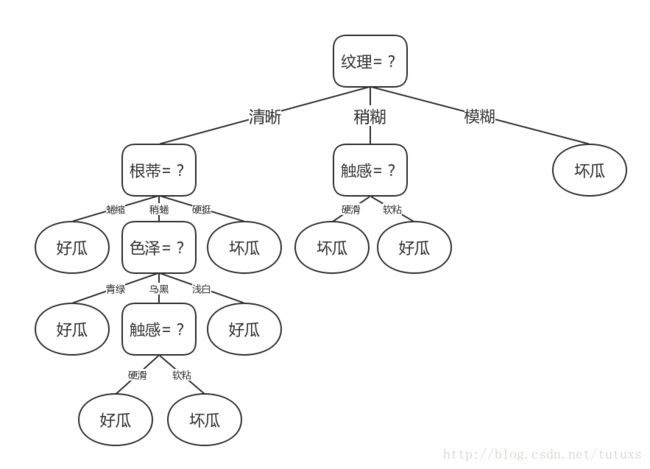
例如:书中的关于西瓜问题的一颗决策树
从这个图可以看出,色泽青绿,根蒂蜷缩,敲声浊响的西瓜为好瓜
关键在于哪里?
随着划分过程不断进行,我们希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的“纯度”越来越高。这句话的意思是说,在树的相同层里,要么好瓜这一类别越多越好,要么坏瓜这一类别越多越好。
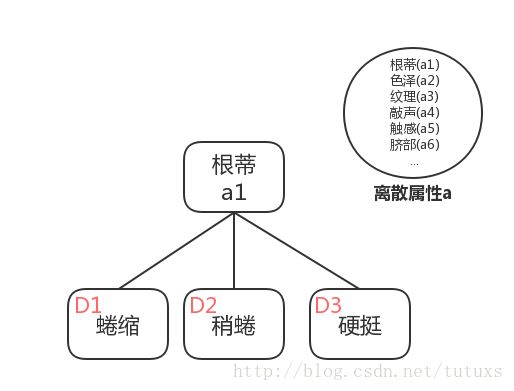
例如上图中,西瓜根蒂的分类有:蜷缩,稍蜷和硬挺。
这里可以打一个比方:足球比赛中,一般会把多个球队分在同一个小组,如果一个小组中的各支球队实力都相当,那么小组出线的可能性就难于预测,如果各个球队的实力差距相当悬殊,那么实力较强的球队出线的可能性会相当大。
同样的道理我们希望每一个分支下面的类别(即好瓜和坏瓜)尽可能属于同一类别,如果同一类别更多,换句话说就是该类别实力比较强,依据该属性(根蒂)分类得出的结果也就更加可靠(明确)。
基本概念
信息熵(information entropy)
在信息论与概率统计中,熵是表示随机变量不确定性的度量,熵越大,随机变量的不确定性就越大。信息熵是度量样本集合“纯度”最常用的一种指标。假定当前样本集合D中第k类样本所占比例为
注意:
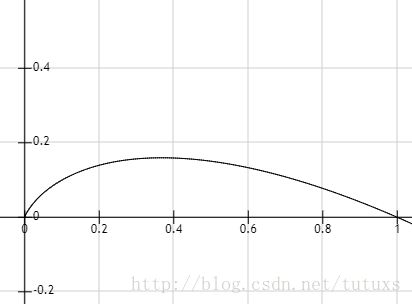
由
当超过0.4的时候,随着
结论:Ent(D)的值越小,则D的纯度越高。
信息增益(information gain)
信息增益表示得到特征X的信息而使得类Y的信息的不确定性减少的程度。假定离散属性a有V个可能值
于是可计算出用属性a对样本集D进行划分所获得的“信息增益”
一般而言,信息增益越大,则意味着使用属性a来划分所获得的“纯度提升”越大。著名的ID3决策树学习算法就是更具信息增益为准则来选择划分属性的。
由于信息增益准则对对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响著名的C4.5决策树算法不直接使用信息增益,而是使用“增益率”来选择最优划分属性。
增益率(gain ratio)
其中
“IV(a)”称为属性a的“固有值”,属性a的可能性数目越多(即V越大),则IV(a)的值通常会越大。
需要注意的是,增益率准则对可能取值数目较少的属性有所偏爱,因此,C4.5算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
数据集
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 好瓜 |
|---|---|---|---|---|---|---|---|
| 1 | 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 2 | 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 3 | 乌黑 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 4 | 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 5 | 浅白 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 6 | 青绿 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 是 |
| 7 | 乌黑 | 稍蜷 | 浊响 | 清糊 | 稍凹 | 软粘 | 是 |
| 8 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 硬滑 | 是 |
| 9 | 乌黑 | 稍蜷 | 沉闷 | 清糊 | 稍凹 | 硬滑 | 否 |
| 10 | 青绿 | 硬挺 | 清脆 | 清晰 | 平坦 | 软粘 | 否 |
| 11 | 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 否 |
| 12 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 软粘 | 否 |
| 13 | 青绿 | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 14 | 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 15 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 否 |
| 16 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 否 |
| 17 | 青绿 | 蜷缩 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
有兴趣的话可以自己算下上面给的公式,这里直接套用书的算式。
利用该数据预测是不是好瓜,显然
所以:
ID3算法
基于信息增益生成的决策树图
伪代码:
这里直接使用了书上的:
输入:训练集 D = {(x1, y1), (x2, y2), ... , (xm, ym)}
属性集 A = {a1, a2, ... , ad}.
过程:函数 TreeGenerate(D, A)
生成结点node;
if D中样本全属于同一类别C then
将node标记为C类叶结点; return
end if
if A == ∅ (OR D中样本在A上取值相同) then
将node标记为叶结点,其类别标记为D中样本数最多的类; return
end if
从A中选择最优划分属性a*;
for a* 的每一个值 a*_v do
为node生成一个分支;令Dv表示D中在a*上取值为a*_v的样本子集;
if Dv 为空 then
将分支结点标记为叶结点,其类别标记为D中样本最多的类;then
else
以TreeGenerte(Dv, A \ {a*})为分支结点
end if
end for
输出:以node为根节点的一颗决策树首先我们来理解下训练集中的x和y分别代表什么
- 训练集D:表示上面所给的数据集
- (x, y) : 表示一个训练数据元素。例如:上面的数据集中有17个数据元素
- x:表示数据元素中除了目标属性的属性集(是一个向量)。(例如编号为1的西瓜:青绿,蜷缩,浊响,清晰,凹陷,硬滑)
- y:表示目标属性。(例如上面数据集中的好瓜属性,编号为1的好瓜属性为是)
- 属性集A:表示除目标属性外,供算法学习测试使用的其它属性。(例如:色泽,根蒂,敲声,纹理,脐部,触感)
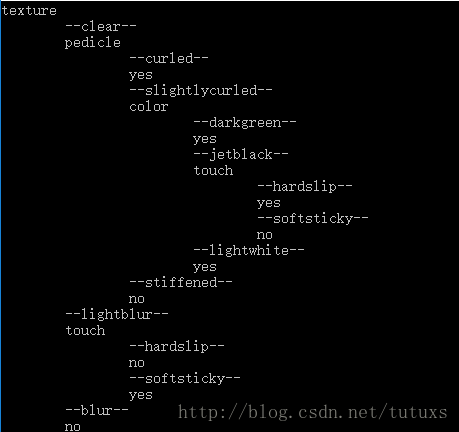
由于C++不像matlab这类语言,所以对数据的处理相对来说会麻烦很多。我将数据进行修改,对应为
- 色泽 : color
- 青绿 : darkgreen
- 乌黑 : jetblack
- 浅白 : lightwhite
- 根蒂 : pedicle
- 蜷缩 : curled
- 稍蜷 : slightlycurled
- 硬挺 : stiffened
- 敲声 : sound
- 浊响 : turbid
- 沉闷 : dull
- 清脆 : crisp
- 纹理 : texture
- 清晰 : clear
- 稍糊 : slightblur
- 模糊 : blur
- 脐部 : umbilical
- 凹陷 : sunken
- 稍凹 : slightlysunken
- 平坦 : flat
- 触感 : touch
- 硬滑 : hardship
- 软粘 : softsticky
C++ 实现
// ID3决策算法 -- 西瓜决策树
TreeRoot TreeGenerate(TreeRoot pTree, // 决策树
std::vector效果图
完整代码:ID3算法
C4.5算法
伪代码
由于ID3算法和C4.5算法的主要区别在于如何选择最优划分属性
输入:训练集 D = {(x1, y1), (x2, y2), ... , (xm, ym)}
属性集 A = {a1, a2, ... , ad}.
过程:函数 TreeGenerate(D, A)
生成结点node;
if D中样本全属于同一类别C then
将node标记为C类叶结点; return
end if
if A == ∅ (OR D中样本在A上取值相同) then
将node标记为叶结点,其类别标记为D中样本数最多的类; return
end if
从A中选择最优划分属性a*;
for a* 的每一个值 a*_v do
为node生成一个分支;令Dv表示D中在a*上取值为a*_v的样本子集;
if Dv 为空 then
将分支结点标记为叶结点,其类别标记为D中样本最多的类;then
else
以TreeGenerte(Dv, A \ {a*})为分支结点
end if
end for
输出:以node为根节点的一颗决策树C++ 实现
这里主要写出划分最优
// 选出最优属性a*
// 返回值为一个std::pair类型,first表示该属性,second表示该属性的映射关系
std::pair<std::string, std::vector<std::string>> optimal_attribute(std::vector其中计算
// 计算Gain(D, a)
double calculate_information_gain(std::vector完整代码:C4.5算法
另:决策树里还有剪枝处理(一种解决“过拟合”的方法),使用连续与缺失值,多变量决策树等等。可以自行深入了解