2020华为软挑热身赛代码开源-思路大起底（华为软件精英挑战赛编程闯关）

本文首发于个人公众号【两猿社】，后台回复【华为】，获取完整开源代码链接。

昵称：lou_shang_shi_bian_tai
成绩:0.032

社长没有针对硬件做任何优化，热身赛成绩也一般。但有些比赛的trick我想与大家一起分享，希望对继续参加初赛的小伙伴有所帮助。

本文内容分为6部分，其中01结合流程图对整体思路进行概述，02-05结合代码对具体模块进行分析，每一部分结束会有一些小trick。

trick是个人测试后的建议，不是理论角度的建议。

目录

• 00 写在前面
• 01 整体思路
• 02 数据读取与转换
• 03 模型训练
• 04 模型预测
• 05 结果文件生成

---

00 写在前面

有人参赛为了奖品，有人参赛为了绿卡，而我，可能是唯一一个参赛为了写公众号的选手→_→。

一周前Web服务器项目详解的推文中，社长曾提到不再参加初赛，热身赛结束后，会将代码开源。

为此，特来填坑。

---

01 整体思路

有关热身赛题目解析与前期踩坑，这里不再赘述，有兴趣的同学可以点击查看2020华为软挑热身赛-这些坑我帮你踩过了。

赛题简述

通俗讲，赛题打算通过研究现有数据的规律，然后对新数据进行二分类。

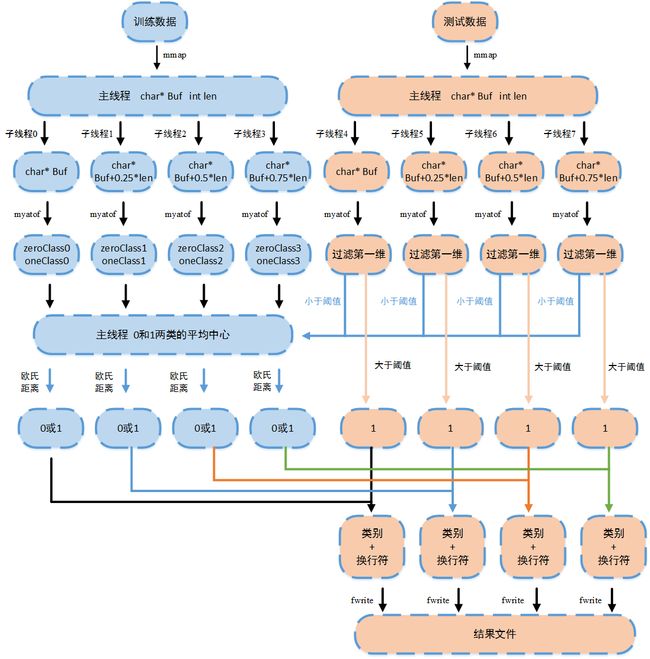
思路流程图

赛题大体上可以分为四部分，数据读取与转换，模型训练，模型预测和结果文件生成。

• 数据读取与转换
  • 主线程通过mmap对文件进行映射，得到数据指针
  • 四个线程从指针四等分处对字节进行处理，通过自己编写的myatof函数转为具体数据
• 模型训练
  • 极其简化的K-Means分类，使用1000个特征维度
  • 子线程读取训练文件的四部分，主线程得到0和1两个类别的平均中心
• 模型预测
  • 将测试文件进行读取与转换，设置阈值对第一个维度的数据进行过滤
  • 小于阈值的使用类别中心和欧氏距离对该行数据进行分类，大于阈值的直接赋值为类别1
• 结果文件生成
  • 模型预测时生成的类别类型为char，而不是int型
  • 每行数据预测后，生成类别+换行符，主线程通过fwrite写入文件

---

02 数据读取与转换

数据读取部分，主线程通过mmap获取数据指针和所有字节数，四个子线程将指针偏移到四等分处，向后解析数据。

//open获取文件描述符
int fd = open(trainDataPwd.c_str(), O_RDONLY);

//得到所有字节数
int len = lseek(fd, 0, SEEK_END);

//获取数据指针
char *buf = (char *)mmap(NULL, len, PROT_READ, MAP_PRIVATE, fd, 0);

//四个子线程从四等分处向后解析数据
std::thread thread0(readAndCal0, buf);
std::thread thread1(readAndCal1, len, buf);
std::thread thread2(readAndCal2, len, buf);
std::thread thread3(readAndCal3, len, buf);

//等待四个子线程解析完
thread0.join();
thread1.join();
thread2.join();
thread3.join();

数据转换部分，通过观察所有特征数据，可以发现只有0.123和-0.123两种情况，可以针对两种情况对数据进行转码，两者的区别仅仅在于是否有负号。

inline int myatof(char *s)
{
	return (s[0] == '-') ? -1 * (1000 * (s[1] - '0') + 100 * (s[3] - '0') + 10 * (s[4] - '0') +(s[5] - '0')): 
						(1000 * (s[0] - '0') + 100 * (s[2] - '0') + 10 * (s[3] - '0') + (s[4] - '0'));
}

trick

• 经测试，ARM上处理整型数据比浮点型要快
• 可以针对数据特点编写更快的数据转换函数

---

03 模型训练

四个子线程，从mmap得到的数据指针四等分处，向后解析数据。

根据所有字节数做等分后，初始的指针可能不是一行数据的起始位置，这里通过判断当前指针的前一位是否为换行符来确定。

如果不是换行符，则对当前指针向后偏移寻找换行符，并指向下一行数据的起始位置。

void readAndCal(int sum, char *buf)
{
	int offset = sum * 0.75;
	char *p = buf + offset;

	//将开头偏移到一行数据的起始位置
	if (*(p - 1) != '\n')
	{
		while (*p != '\n')
		{
			++p;
		}
		p += 1;
	}
	
	//存储数据转换的临时变量
	char tmp5[5];
	char tmp6[6];
	signed int mmtmp[1000];

	int pthnum = 0;
	
	//每个线程读取训练数据的EVERY个数据，这里EVERY设置为700
	while (pthnum < EVERY)
	{

		//将这一行的数据转码
		int i = 0;
		while (i <= 999)
		{
			//找到逗号,跳过数据,+1跳过逗号
			//两种情况,一种是0.123,一种是-0.123
			switch (*(p + 5) == ',')
			{
			case 0:
				//这里可以直接使用指针偏移对p进行转码，减少临时变量这一步，经测试，效果有限
				//mmtmp[i] = -1 * (1000 * (*(p + 1) - '0') + 100 * (*(p + 3) - '0') + 10 * (*(p + 4) - '0') + (*(p + 5) - '0'));
				memcpy(tmp6, p, 6);
				mmtmp[i] = myatof(tmp6);
				p += 7;
				break;
			case 1:
				memcpy(tmp5, p, 5);
				mmtmp[i] = myatof(tmp5);
				p += 6;
				break;
			}
			++i;
		}

		++pthnum;

		//将类别找到,将当前行的数据求和更新类中心，更新类计数
		switch ((*p - '0') == 0)
		{
		case 0:
			oneNumThree++;
			for (signed int j = 0; j < 1000; ++j)
			{
				oneClassThree[j] += mmtmp[j];
			}
			break;
		case 1:
			zeroNumThree++;
			for (signed int j = 0; j < 1000; ++j)
			{
				zeroClassThree[j] += mmtmp[j];
			}
			break;
		}
		//跳过数据,再跳过\n,到下一行的开始
		p += 2;
	}
}

通过join等到四个子线程处理完，主线程对子线程的各个类数组内的特征值进行平均，得到最终的类中心。

	
//训练数据中，0和1两类的数目
int zeronum = zeroNumZero + zeroNumThree + zeroNumOne + zeroNumTwo;
int onenum = oneNumOne + oneNumTwo + oneNumZero + oneNumThree;

//更新类中心
for (int i = 0; i < 1000; ++i)
{
	zeroClassOne[i] = (zeroClassZero[i] + zeroClassThree[i] + zeroClassTwo[i] + zeroClassOne[i]) / zeronum;
	oneClassOne[i] = (oneClassZero[i] + oneClassThree[i] + oneClassTwo[i] + oneClassOne[i]) / onenum;
}

trick

• switch-case比if-else要快一些
• memcpy比字符数组挨个赋值要快
• 减少训练数据的个数，可以极大减少io时间，从而减少运行时间

---

04 模型预测

将预测文件通过mmap映射到内存，获取数据指针，先对第一维的特征值进行转换并通过阈值过滤，这里的阈值设置为200。

第一个维度的特征值小于阈值时，使用算法进行预测，大于阈值则直接置1。

int len = sum * 0.25;
char *p = buf;
char tmp5[5];
char tmp6[6];

signed int mmtmp[1000];

char *result0 = predict0;

//生成的类别+换行符
char result[2];
result[1] = '\n';

int _mmtmp = 0;

while (*p && p - buf < len)
{
	
	//将这一行的数据转码
	int i = 0;

	switch (*(p + 5) == ',')
	{
	case 0:
		memcpy(tmp6, p, 6);
		mmtmp[i] = myatof(tmp6);
		p += 7;
		break;
	case 1:
		memcpy(tmp5, p, 5);
		mmtmp[i] = myatof(tmp5);
		p += 6;
		break;
	}

	//第一维度数据大于TEST0,直接赋值1,跳过这一行
	switch (mmtmp[i] > TEST0)
	{
	case 0:

		//小于TEST0的使用算法进行预测
		++i;
		while (i <= 998)
		{
			//找到逗号,然后跳过数据,+1跳过逗号
			//两种情况,一种是0.123,一种是-0.123
			switch (*(p + 5) == ',')
			{
			case 0:
				memcpy(tmp6, p, 6);
				mmtmp[i] = myatof(tmp6);
				p += 7;
				break;
			case 1:
				memcpy(tmp5, p, 5);
				mmtmp[i] = myatof(tmp5);
				p += 6;
				break;
			}
			++i;
		}
		
		//经测试数据最后一维为0.123格式
		memcpy(tmp5, p, 5);
		mmtmp[i] = myatof(tmp5);
		p += 6;

		//通过算法预测，返回字符0或1
		result[0] = mmclass(zeroClassOne, oneClassOne, mmtmp);
		memcpy(result0, result, 2);
		++addr;
		result0 += 2;

		break;
	case 1:
		//过滤第一维数据后，跳跃5992个字节，尽快接近末尾换行符
		p += 5992;
		while (p - buf < len && *p != '\n')
		{
			++p;
		}
		p += 1;

		//直接置1
		result[0] = CLASS;
		memcpy(result0, result, 2);
		++addr;
		result0 += 2;

		break;
	}
}

算法部分，计算该行数据1000维特征值与两类中心点的欧氏距离，返回字符0或1。

inline int myabs(int n)
{
	return (n>0)?n:-n;
}

char mmclass(signed int *zeroClass, signed int *oneClass, signed int *test_item)
{
	signed int eulerDisZero = 0, eulerDisOne = 0;
	signed int tmp1 = 0, tmp2 = 0;

	//计算该行数据1000维特征值与两类中心点的欧氏距离
	for (signed int i = 0; i < 1000; ++i)
	{
		tmp1 = myabs(zeroClass[i] - test_item[i]);
		tmp2 = myabs(oneClass[i] - test_item[i]);
		eulerDisZero = eulerDisZero + tmp1 * tmp1;
		eulerDisOne = eulerDisOne + tmp2 * tmp2;
	}

	return eulerDisZero < eulerDisOne ? '0' : '1';
}

trick

• 过滤第一个维度减少预测的数据量
• 若第一维度大于阈值，跳过5992个字节，以过滤该行剩余所有数据

---

05 结果文件生成

结果文件生成时，之前采用文件流，写入int类型和endl换行符，占时较长。之后改为全部写入char类型，提速非常明显。

//获取测试文件的数据指针和所有字节长度
int fd0 = open(testFile.c_str(), O_RDONLY);
int len0 = lseek(fd0, 0, SEEK_END);
char *buf0 = (char *)mmap(NULL, len0, PROT_READ, MAP_PRIVATE, fd0, 0);

//四个子线程对测试文件进行分类
std::thread thread4(readAndCla0, len0, buf0, zeroClassOne, oneClassOne);
std::thread thread5(readAndCla1, len0, buf0, zeroClassOne, oneClassOne);
std::thread thread6(readAndCla2, len0, buf0, zeroClassOne, oneClassOne);
std::thread thread7(readAndCla3, len0, buf0, zeroClassOne, oneClassOne);

//获取结果文件指针
FILE *stream = fopen(predictFile.c_str(), "wb");

//顺序等待子线程运行完，直接写入文件
thread4.join();
fwrite(predict0, sizeof(char), addr * 2, stream);
thread5.join();
fwrite(predict1, sizeof(char), addr1 * 2, stream);
thread6.join();
fwrite(predict2, sizeof(char), addr2 * 2, stream);
thread7.join();
fwrite(predict3, sizeof(char), addr3 * 2, stream);

trick

• 输出到文件中的换行符用endl会超级慢
• 生成类别+换行符，其中类别为char字符

---

最后，预祝大家在后续的比赛中都能取得理想的成绩。

关注公众号【两猿社】，后台回复【华为】，获取完整开源代码链接。

完。

如果你喜欢这篇文章，不妨顺手关注下面公众号哦。