DTW算法

dtw算法主要针对序列匹配提出的，尤其是当序列出现一定的飘移，欧氏距离度量就会失效。dtw常用在语音匹配当中，在图像处理里面也有一定的应用。
现在有两个序列X,Y.
X=[2,3,4,7,9,2,1,2,1],Y=[1,1,1,1,2,3,3,4,7,8,9,1,1,1,1]
绘制在坐标轴上如下图

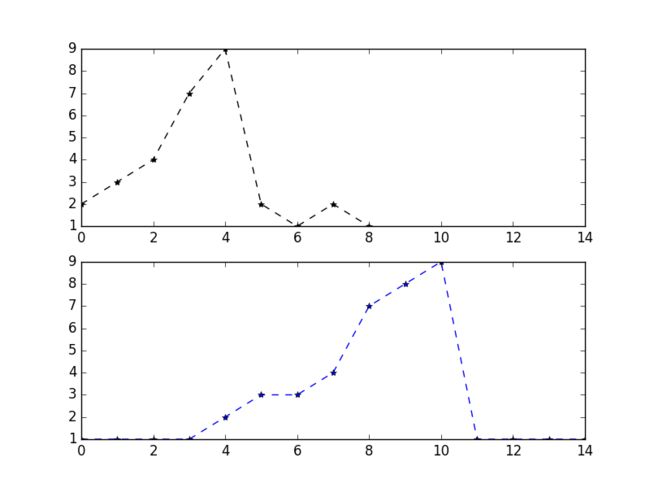
我们可以看到，两个序列的欧氏距离很大，因为两个序列存在横轴上的飘移。dtw算法就是为了解决此类问题，简单的说dtw算法就是将两个序列在某些时点上压缩，实现两个序列之间的“距离”最小，这里这个距离一般使用欧氏距离。
dtw算法本质是寻找一条从X[0],Y[0]到X[N],Y[M]的最短的路径。对于上面给出的序列X,Y。找到的压缩路径是[(0, 0), (0, 1), (0, 2), (0, 3), (0, 4), (1, 5), (1, 6), (2, 7), (3, 8), (4, 9), (4, 10), (5, 11), (6, 11), (6, 12), (6, 13), (6, 14), (7, 14), (8, 14)]。对应的压缩关系绘制成图（有点丑，将就看吧）

说了结果，下面我们来找这个压缩路径。

这个算法有几个约束，但简而言之就是得从X[0],Y[0]走到X[N],Y[M]，即从上图中的左下角走到右上角。
贪心算法，并不能求得全局最优解，刚开始把这个问题做成了贪心算法，后来想想不太对，就去恶补了动态规划。下面是贪心算法的错误求解。
每走一步，都是选择距离增加最少的走，并且只有三个方向，向上，向右，向斜对角。这样就保证不会往回走已经走过的路径。假设X,Y构成的N*M的矩阵是距离矩阵D，如上图。那么我们从D[0][0]点走到D[9][14]（有9列，14行（这里以列为主序）)。那么我们开始计算前几步该如何走，D[0][0]=abs(Y[0]-X[0])=1,，下一步有三个方向，向上D[0][1]=D[0][0]+abs(Y[1]-X[0])=2,向右D[1][0]=D[0][0]+abs(Y[0]-X[1])=3,向斜对角D[1][1]=D[0][0]+abs(Y[1]-X[1])=3。取距离最小，所以选择向上，依次类推，最后得到上图的结果，这就是压缩路径，最终两个序列之间的距离是7。ps:中间可能会遇到向上，向右，像斜上方的距离相等的情况，那么随便选择一个方向即可，路径不一样，但是最终的距离都是相等的。
按照自己思路写出dtw算法如下，时间复杂度是O(N+M)。

def Distance(x,y):
    return abs(x-y)
def Dtw(X,Y):
    Lx=len(X)
    Ly=len(Y)
    D=[[sys.maxint for i in range(Lx)]for j in range(Ly)]
    minD=0
    j=0
    k=0
    path=[(0,0)]
    for i in range(Lx+Ly):
        if (j == Ly-1) and (k == Lx-1):
            break
        elif (j==Ly-1) and (k != Lx-1):
            k += 1
            D[j][k]=D[j][k-1]+Distance(Y[j],X[k])
        elif (j != Ly-1) and (k == Lx-1):
            j += 1
            D[j][k]=D[j-1][k]+Distance(Y[j],X[k])
        else:
            if j==0 and k==0:
                D[j][k]=Distance(Y[j],X[k])
            D[j+1][k]=Distance(Y[j+1],X[k])+D[j][k]
            D[j][k+1]=Distance(Y[j],X[k+1])+D[j][k]
            D[j+1][k+1]=Distance(Y[j+1],X[k+1])+D[j][k]
            if(D[j+1][k]1]):
                minD=D[j+1][k]
                if(minD>D[j+1][k+1]):
                    j += 1
                    k += 1
                else:
                    j += 1
            else:
                minD=D[j][k+1]
                if(minD>D[j+1][k+1]):
                    j += 1
                    k += 1
                else:
                    k += 1
        path.append((k,j))
        minD=D[j][k]
    return minD,path

动态规划
仔细分析，其实该过程的最优解用dp可以实现，状态转换方程为
D(i,j)=M[i][j]+min(D[i-1][j],D[i][j-1],D[i-1][j-1])。

def dtw(X,Y):
    Lx=len(X)
    Ly=len(Y)
    path=[]
    M=[[Distance(X[i],Y[j]) for i in range(Lx)]for j in range(Ly)]
    D=[[0 for i in range(Lx+1)]for j in range(Ly+1)]
    D[0][0]=0
    for i in range(1,Lx+1):
        D[0][i]=sys.maxint
    for j in range(1,Ly+1):
        D[j][0]=sys.maxint
    for i in range(1,Ly+1):
        for j in range(1,Lx+1):
            D[i][j]=M[i-1][j-1]+min(D[i-1][j],D[i-1][j-1],D[i][j-1])
    minD=D[Ly][Lx]
    return minD