机器学习-学习笔记-梯度下降-SGD/BGD

根据Andrew Ng的Lecture notes, 我重新整理了梯度下降（including LMS/BGDSGD）的相关知识。

首先，引入一个例子，
假设我们现在有一个数据集，数据集中包含了A城市的47套房屋的信息，信息有房屋的居住面积，房间数量和价格，数据集如下图。我们要做的是，根据房屋的居住面积和房间数量来预测它的价格。

简单的以 x1 表示房屋的居住面积， x2 来表示房屋的房间数量，以 y 来表示房屋的价格。
进一步表示，
xi1 表示数据集中第 i 套房屋的居住面积
xi2 表示数据集中第 i 套房屋的房间数量

假设 x1,x2 和 y 是线性关系，现在我们要通过 x1,x2 来预测 y ，我们用：

hθ(x)=θ0+θ1x1+θ2x2

来表示 x1,x2 的线性函数，其中 θ1,θ2 都是这个函数的参数，称作权值(weights).
为了求出y的值，首先我们随机给 θ1,θ2 附值，计算 hθ(x) ，然

好了，现在我们的问题转化成了怎么让 hθ(x) 尽可能的接近y。

首先，我们用一个函数来表示 hθ(x) 和 y 的接近程度， J(θ) 表示接近程度

J(θ)=12∑i=1m(hθ(xi)−yi)2

这个公式来源于数学中学习过的最小二乘法OLS(Ordinary least squares)。

J(θ) 是 hθ(x) 和 y 的接近程度，我们想要让 hθ(x) 尽可能的接近 y ，也就是要找到 J(θ) 的最小值，LMS算法就是用来寻找这个最小值的.

LMS算法

来，先看一幅图，

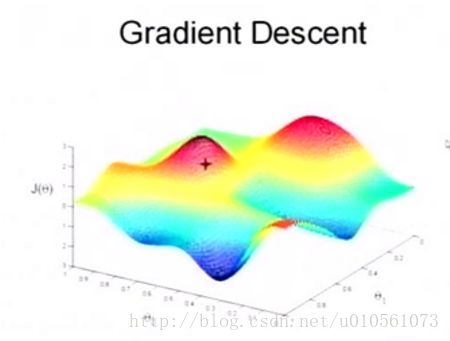
这是一幅3D图，水平平面的横纵轴分别是 θ1,θ2 的值，垂直轴是 J(θ) 的值，我们要找到图中最小的 J(θ) 对应的 θ1,θ2 值。

下面我来介绍一下LMS算法的概念，我们把这幅图想象成一座山，我们是站在山上某个位置的人，我们的目的是找到这座山的最低点。
首先我们随机选取一个起点，如图的+号位置作为我们现在在山上的位置，然后我们每一次沿着最陡的方向往下走一步，迈的步伐大小设为α，我们不停地朝着最陡的方向下山，直到到达一个局部最低点（周围没有更低的地方），这也就是梯度下降GD（gradient descent）的思想。

下面我们用数学公式来表示LMS算法，

高等数学里讲过，偏导数是函数值变化最快的方向，在我们这个例子里，也就是我们在山上站立位置周围下山最陡的方向。
进一步解这个函数，

那么对于数据集中的每一座房屋，

θj:=θj+α(y(i)−hθ(x(i)))x(i)j

这就是LMS每一次更新的原则，也称作Widrow-Hoff学习法则。

只使用单座房屋的j的计算方式并不能求出 J(θ) 的最小值，为了通过全部的房屋数据来调整 θj ，我们引入了批量梯度下降BGD(batch gradient descent)和随机梯度下降SGD(stochastic gradient descent)。

批量梯度下降

批量梯度下降中 θj 的计算方式为，对于每一个 j , 计算下列公式直至收敛,

θj:=θj+α∑i=1m(y(i)−hθ(x(i)))x(i)j

也就是每一次选择下降方向时，我们要把所有的房屋数据计算一遍。
批量梯度下降可以找到一个全局最优解，如下图。但是如果数据集量过大，那么那么迭代速度会极其极其慢。

随机梯度下降

随机梯度下降中 θj 的计算方式为，每一次下降时，只选择一座房屋数据来计算 θj ，公式如下图：

随机梯度下降不能精确地收敛到全局最小值，但是在数据量过大的时候，这种方法更快。