B-树(B树)
一,B-树就是B树
英文名字叫做B-tree,中间的短线是英文连接符,只是翻译的时候将短线翻译成了减号。
全称Balance-tree(平衡多路查找树),平衡的意思是左边和右边分布均匀。多路的意思是相对于二叉树而言的,二叉树就是二路查找树,查找时只有两条路,而B-tree有多条路,即父节点有多个子节点。
二,B-树用途
使用B-tree结构可以显著减少定位记录时所经历的中间过程,从而加快存取速度。这个数据结构一般用于数据库的索引,综合效率较高。
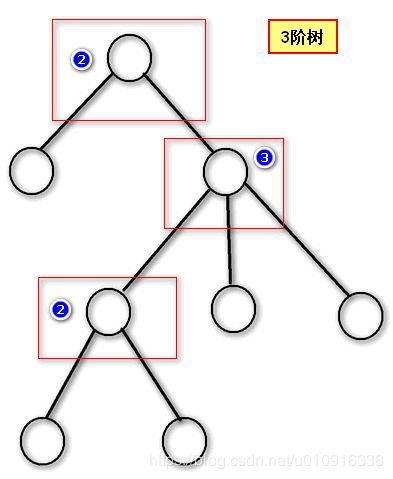
三,阶的概念
对于一棵m阶B-tree,每个结点至多可以拥有m个子结点。
即遍观整棵树,子节点最多的个数是m,那么这棵树就是m阶树。
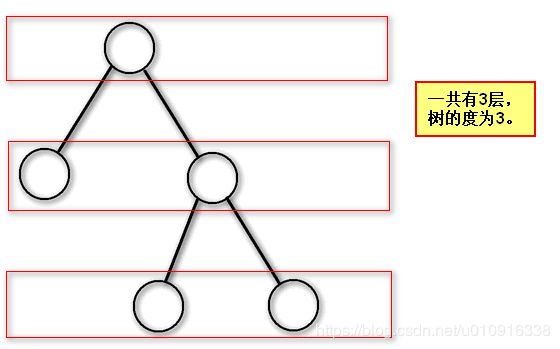
四,树的度
树的度就是树的高度,即树的层数。
下图以二叉树为例,其他类型数与此相同。
五,B-树的定义
(1)树中每个结点至多有m 棵子树(注:m指的是树的阶);
(2)若根结点不是叶子结点,则至少有两棵子树(注:根节点至少有两个儿子);
(3)除根结点之外的所有非叶子结点至少有p个子节点(![]() ,
, ![]() 为向上取整。);
为向上取整。);
(4)所有的非叶子结点中包含以下数据:(n,A0,K1,A1,K2,…,Kn,An)
其中:
Ki(i=1,2,…,n)为关键码,且Ki
Ai 为指向儿子的指针(i=0,1,…,n),且指针Ai-1 所指子树中所有结点的关键码均小于Ki (i=1,2,…,n),An 所指子树中所有结点的 关键码均大于Kn。(注:每个ki数据两旁各安放了一个指针,即Ai-1和Ai,左边的子树数据统统小于ki,右边子树的数据统 统大于ki)(注:总体来看指针数量比数据数量多1)
n 为关键码的个数(![]() )。
)。
(5)所有的叶子结点都出现在同一层次上,即所有叶节点具有相同的深度,等于树高度。并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
六,B-树和二叉树的不同点
(1)二叉树节点中保存的数据只有一个,而B-树得节点中保存的是线性表,真实数据数据不止一个有很多。由于表中的指针和子节点一一对应,而子节点个数又有限定(![]() ,
, ![]() 为向上取整。),又因为真实数据数量又比指针少一个所以真实数据也就有了限定(
为向上取整。),又因为真实数据数量又比指针少一个所以真实数据也就有了限定(![]() )。
)。
(2)二叉树至多有两个儿子节点,而B-树至多有m个节点(m为树的阶)
七,B-树的查找
B-树的查找类似二叉排序树的查找,不同的是B-树每个结点上是多关键码的有序表,在到达某个结点时,先在有序表中查找,若找到,则查找成功;否则,到按照对应的指针信息指向的子树中去查找,当到达叶子结点时,则说明树中没有对应的关键码。
举例:
如下图是一棵四阶B-树,其深度为4(注:阶和度没有关系,此图刚好阶和度相等), 在图一中查找关键字47过程如下:
![]()
图一
(1)首先从根节点a开始,因为 a 节点中只有一个关键字35,且给定值47 > 关键字35,则若存在必在指针A1所指的子树内。
(2)顺指针找到 c节点,该节点有两个关键字(43和 78),而43 < 47 < 78,若存在比在指针A1所指的子树中。
(3)同样,顺指针找到 g节点,在该节点找到关键字47,查找成功。
八,B-树的插入
举例:
如图(a) 为3阶的B-树(图中略去F结点(即叶子结点)),假设需依次插入关键字30,26,85。
![]()
(1)首先通过查找确定插入的位置。由根节点a开始查找,确定30应插入的在d 节点中。由于d 中关键字数目不超过2(即m-1),故第一个关键字插入完成:如图(b)
![]()
(2)同样,通过查找确定关键字26亦应插入 d, 由于d节点关键字数目超过2,此时需要将 d分裂成两个节点,关键字26及其前、后两个指针仍保留在 d 节点中。而关键字37 及其前、后两个指针存储到新的产生的节点 d` 中。同时将关键字30 和指示节点 d `的指针插入到其双亲的节点中。由于 b节点中的关键字数目没有超过2,则插入完成.如(c)(d)
![]()
![]()
(3) (e) -(g) 为插入85后;
![]()
![]()
![]()
九,B-树的删除