PCA - python实现（二）

一、简单概念介绍

1.1 numpy 的 .std() 和 pandas 的 .std() 函数之间是不同的

  默认情况下，numpy 计算的是总体标准偏差，ddof = 0。另一方面，pandas 计算的是样本标准偏差，ddof = 1。如果我们知道所有的分数，那么我们就有了总体——因此，要使用 pandas 进行归一化处理，我们需要将“ddof”设置为 0。

在统计学中，多年的经验总结出：

• 如是总体,标准差公式根号内除以 n，
• 如是样本,标准差公式根号内除以 （n-1），
• 因为我们大量接触的是样本,所以普遍使用根号内除以（n-1)。

公式意义 ：所有数减去平均值,它的平方和除以数的个数（或个数减一),
再把所得值开根号,就是1/2次方,得到的数就是这组数的标准差。

1.2 np.linalg.svd()

函数：np.linalg.svd(a,full_matrices=1,compute_uv=1)

• np.linalg.inv()：矩阵求逆
• np.linalg.det()：矩阵求行列式（标量）
• SVD（Singular Value Decomposition，奇异值分解）是一种因子分解运算，将一个矩阵分解为3个矩阵的乘积，**np.linalg.svd()**函数返回3个矩阵——U、Sigma和V，其中U和V是正交矩阵，Sigma包含输入矩阵的奇异值。
• 使用diag函数生成完整的奇异值矩阵。将分解出的3个矩阵相乘U * np.diag(Sigma) * V
• np.diag(array) 返回一个矩阵的对角线元素，或者创建一个对角阵
    array是一个1维数组时，结果形成一个以一维数组为对角线元素的矩阵
    array是一个二维矩阵时，结果输出矩阵的对角线元素

import numpy as np
a = np.arange(1, 4)
b = np.arange(1, 10).reshape(3, 3)
print('np.diag(a)',np.diag(a))
print('np.diag(b)',np.diag(b))
'''结果
np.diag(a) [[1 0 0]
 [0 2 0]
 [0 0 3]]
np.diag(b) [1 5 9]
'''

参数：

• a是一个形如(M,N)矩阵
• full_matrices的取值是为0或者1，默认值为1，这时u的大小为(M,M)，v的大小为(N,N) 。否则u的大小为(M,K)，v的大小为(K,N) ，K=min(M,N)。
• compute_uv的取值是为0或者1，默认值为1，表示计算u,s,v。为0的时候只计算s。

返回值：

总共有三个返回值u,s,v
u大小为(M,M)，s大小为(M,N)，v大小为(N,N)。

                 A = u * s * v

  其中s是对矩阵a的奇异值分解。s除了对角元素不为0，其他元素都为0，并且对角元素从大到小排列。s中有n个奇异值，一般排在后面的比较接近0，所以仅保留比较大的r个奇异值。
  注 因为sigma是除了对角元素不为0，其他元素都为0。所以返回的时候，作为一维矩阵返回。本来sigma应该是由3个值的，但是因为最后一个值为0，所以直接省略了。

import numpy as np
D = np.mat('4 11 14;8 7 -2')
U,Sigma,V = np.linalg.svd(D,full_matrices=False)
print('U,Sigma,V',U,Sigma,V)
print ('U * np.diag(Sigma) * V',U * np.diag(Sigma) * V)
'''结果
U,Sigma,V 
[[-0.9486833  -0.31622777][-0.31622777  0.9486833 ]] 
[18.97366596  9.48683298] 
[[-0.33333333 -0.66666667 -0.66666667][ 0.66666667  0.33333333 -0.66666667]]
U * np.diag(Sigma) * V 
[[ 4. 11. 14.]
 [ 8.  7. -2.]]
'''

1.3 PCA的应用

1. 数据压缩

• 数据压缩或者数据降维首先能够减少内存或者硬盘的使用， 如果内存不足或者
  计算的时候出现内存溢出等问题， 就需要使用PCA获取低维度的样本特征。
• 其次， 数据降维能够加快机器学习的速度。

2. 数据可视化
  在很多情况下， 可能我们需要查看样本特征， 但是高维度的特征根本无法观察， 这个时候我们可以将样本的特征降维到2D或者3D， 也就是将样本的特征维数降到 2个特征或者3个特征， 这样我们就可以采用可视化观察数据。

二、PCA 计算过程

2.1 Feature Normalization 特征归一化

  首先要对训练样本的特征进行归一化， 特别强调的是， 归一化操作只能在训练样本中进行， 不能才CV集(验证集)合或者测试集合中进行， 也就是说归一化操作计算的各个参数只能由训练样本得到， 然后测试样本根据这里得到的参数进行归一化， 而不能直接和训练样本放在一起进行归一化。
  另外， 在训练PCA降维矩阵的过程中，也不能使用CV样本或者测试样本， 这样做是不对的。 有很多人在使用PCA训练降维矩阵的时候， 直接使用所有的样本进行训练， 这样实际上相当于作弊的， 这样的话降维矩阵是在包含训练样本和测试样本以及CV样本的情况下训练得到的， 在进行测试的时候， 测试样本会存在很大的优越性， 因为它已经知道了要降维到的空间情况。

X = (X - X.mean()) / X.std()

2.2 计算降维矩阵

2.2.1 首先计算样本特征的协方差矩阵

X = np.matrix(X)
cov = (X.T* X) / X.shape[0]
# cov是(M,N)

2.2.2 计算协方差矩阵的特征值和特征向量

U, S, V = np.linalg.svd(cov)
# 返回值u(M,M),s(M,N),v(N,N)
# 因为sigma是除了对角元素不为0，其他元素都为0。所以返回的时候，作为一维矩阵返回。本来
# sigma应该是由3个值的，但是因为最后一个值为0，所以直接省略了。

  U 则是计算得到的协方差矩阵的所有特征向量， 每一列都是一个特征向量， 并且特征向量是根据特征大小由大到小进行排序的， U 的维度为 n * n 。 U 也被称为降维矩阵。 利用U 可以将样本进行降维。 默认的U 是包含协方差矩阵的所有特征向量， 如果想要将样本降维到 k 维， 那么就可以选取 U 的前 k 列， Uk 则可以用来对样本降维到 k 维。 这样 Uk 的维度为 n * k

2.3 降维计算

  获得降维矩阵后， 即可通过降维矩阵将样本映射到低维空间上。X 是 m * n的， 那么降维后就变为 m * k 的维度， 每一行表示一个样本的特征。

# k是要降的维度
def project_data(X, U, k):
    U_reduced = U[:,:k]
    return np.dot(X, U_reduced)
    

2.4 贡献率 （降维的k的值的选择）

  k 越大， 也就是使用的U 中的特征向量越多， 那么导致的降维误差越小， 也就是更多的保留的原来的特征的特性。 反之亦然。
  从信息论的角度来看， 如果选择的 k 越大， 也就是系统的熵越大， 那么就可以认为保留的原来样本特征的不确定性也就越大， 就更加接近真实的样本数据。 如果 k 比较小， 那么系统的熵较小， 保留的原来的样本特征的不确定性就越少， 导致降维后的数据不够真实。
  因为在 对协方差矩阵进行奇异值分解的时候返回了 S , S 为协方差矩阵的特征值， 并且 S 是对角矩阵， 维度为 n * n， 计算 k 的取值如下：

差异性的百分比:就是前 k 个特征值之和除以所有的特征值之和也就是特征值的总和比上前K个特征值，一般来说贡献率要大于95%才不影响表达原始数据。

三、python 实现

3.1 二维的PCA

数据下载：
链接：https://pan.baidu.com/s/1eCLjOP45R3TEvAqKWuK9Hg
提取码：qppx

# coding = utf-8
# 2019/7/29  Luckyxxt：有趣的事，Python永远不会缺席！
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
data = loadmat('./PCA/data/ex7data1.mat')
print('data.keys:',data.keys())
# data.keys: dict_keys(['__header__', '__version__', '__globals__', 'X'])
X = data['X']
print('X.shape',X.shape)#(50, 2)

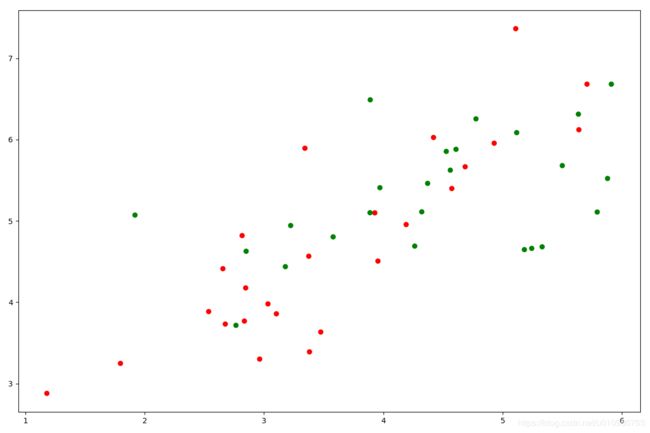
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(1,1,1)
ax1.scatter(X[:,0],X[:,1],c=['r','g'])
plt.show()

# PCA的算法相当简单。 在确保数据被归一化之后，输出仅仅是原始数据的协方差矩阵的奇异值分解。
print('type(X)',type(X))#type(X) 
print('X.mean()',X.mean())#平均值X.mean() 4.496035565920988
print('X.std()',X.std())#标准差X.std() 1.201784846469418

def pca(X):
    # normalize the features
    X = (X - X.mean()) / X.std()

    # compute the covariance matrix
    X = np.matrix(X)
    print('type(X)',type(X),X.shape)#type(X)  (50, 2)
    cov = (X.T* X) / X.shape[0]#cov.shape (2, 2)
    print('cov.shape',cov.shape)
    # perform SVD  cov是(M,N)
    U, S, V = np.linalg.svd(cov)#返回值u(M,M),s(M,N),v(N,N)
    #因为sigma是除了对角元素不为0，其他元素都为0。所以返回的时候，作为一维矩阵返回。本来sigma应该是由3个值的，但是因为最后一个值为0，所以直接省略了。
    print('U.shape, S.shape, V.shape', U.shape, S.shape, V.shape)#(2, 2) (2,) (2, 2)
    return U, S, V

U, S, V = pca(X)
print('U, S, V',U, S, V)
# 现在我们有主成分（矩阵U），我们可以用这些来将原始数据投影到一个较低维的空间中。
# 对于这个任务，我们将实现一个计算投影并且仅选择顶部K个分量的函数，有效地减少了维数。

def project_data(X, U, k):
    U_reduced = U[:,:k]
    print('U_reduced.shape',U_reduced.shape)#U_reduced.shape (2, 1)
    return np.dot(X, U_reduced)

Z = project_data(X, U, 1)
print('Z',Z.shape)#(50, 1)#二维数据降到了一维

3.2 多维PCA用于面部数据

# coding = utf-8
# 2019/7/29  Luckyxxt：有趣的事，Python永远不会缺席！
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
faces = loadmat('./PCA/data/ex7faces.mat')
print('faces.keys()',faces.keys())
X = faces['X']
print('X.shape',X.shape)
# faces.keys() dict_keys(['__header__', '__version__', '__globals__', 'X'])
# X.shape (5000, 1024)

# 渲染数据集中的前100张脸的函数

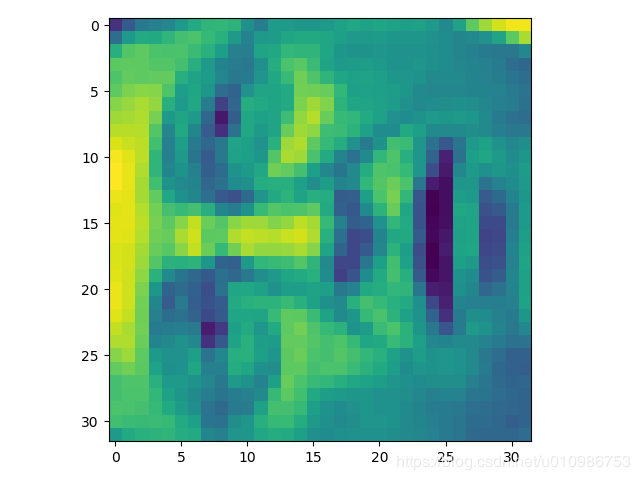
face = np.reshape(X[3,:], (32, 32))
# 看起来很糟糕。 这些只有32 x 32灰度的图像（它也是侧面渲染，但我们现在可以忽略）。
# 我们的下一步是在面数据集上运行PCA，并取得前100个主要特征。
plt.imshow(face)
plt.show()

def pca(X):
    # normalize the features
    X = (X - X.mean()) / X.std()

    # compute the covariance matrix
    X = np.matrix(X)
    print('type(X)',type(X),X.shape)#type(X)  (50, 2)
    cov = (X.T* X) / X.shape[0]#cov.shape (2, 2)
    print('cov.shape',cov.shape)
    # perform SVD  cov是(M,N)
    U, S, V = np.linalg.svd(cov)#返回值u(M,M),s(M,N),v(N,N)
    #因为sigma是除了对角元素不为0，其他元素都为0。所以返回的时候，作为一维矩阵返回。本来sigma应该是由3个值的，但是因为最后一个值为0，所以直接省略了。
    print('U.shape, S.shape, V.shape', U.shape, S.shape, V.shape)#(2, 2) (2,) (2, 2)
    return U, S, V

def project_data(X, U, k):
    U_reduced = U[:,:k]
    return np.dot(X, U_reduced)

U, S, V = pca(X)
Z = project_data(X, U, 100)
print('Z.shape',Z.shape)#Z.shape (5000, 100)

四、 重构原数据

  重构reconstruction， 根据降维后数据重构原数据，即数据还原。

def recover_data(Z, U):
    m, n = Z.shape

    if n >= U.shape[0]:
        raise ValueError('Z dimension is >= U, you should recover from lower dimension to higher')

    return Z @ U[:, :n].T

有趣的事，Python永远不会缺席

欢迎关注小婷儿的博客

    文章内容来源于小婷儿的学习笔记，部分整理自网络，若有侵权或不当之处还请谅解

    如需转发，请注明出处：小婷儿的博客python    https://www.cnblogs.com/xxtalhr/

博客园 https://www.cnblogs.com/xxtalhr/

CSDN https://blog.csdn.net/u010986753

有问题请在博客下留言或加作者：
     微信：tinghai87605025 联系我加微信群
     QQ ：87605025
     python QQ交流群：py_data 483766429

培训说明

OCP培训说明连接 https://mp.weixin.qq.com/s/2cymJ4xiBPtTaHu16HkiuA

OCM培训说明连接 https://mp.weixin.qq.com/s/7-R6Cz8RcJKduVv6YlAxJA

     小婷儿的python正在成长中，其中还有很多不足之处，随着学习和工作的深入，会对以往的博客内容逐步改进和完善哒。重要的事多说几遍。。。。。。