常见聚类(K-means、DSCAN)算法及实现
文章目录
- K-means
- K-means
- k值如何确定
- K-mediods(K中心点)算法
- 层次聚类
- 密度聚类
- DSCAN
- 谱聚类
- 常用的评估方法:轮廓系数(Silhouette)
- 相似度度量及相互系数
K-means
K-means
K-means算法优点:
1).是解决聚类问题的一种经典算法,原理简单,实现容易。
2).当簇接近高斯分布时,它的效果较好。
3).与密度聚类中的DSCAN相比,簇与簇之间划分清晰。
4). 可作为其他聚类方法的基础算法,如谱聚类。
K-means算法缺点:
1).在簇的平均值可被定义的情况下才能使用,可能不适用于某些应用。
2).在K-means算法中K是事先给定的,这个K值的选定是非常难以估计的。很多时候,事先并不知道给定的数据集应该分成多少个类别才最合适。
3).在 K-means 算法中,首先需要根据初始聚类中心来确定一个初始划分,然后对初始划分进行优化。这个初始聚类中心的选择对聚类结果有较大的影响,一旦初始值选择的不好,可能无法得到有效的聚类结果。
4).该算法需要不断地进行样本分类调整,不断地计算调整后的新的聚类中心,因此当数据量非常大时,算法的时间开销是非常大的。
5).若簇中含有异常点,将导致均值偏离严重(即:对噪声和孤立点数据敏感)。
6).不适用于发现非凸形状的簇或者大小差别很大的簇。
7). 结果不一定是全局最优,只能保证局部最优
8). 算法时间复杂度比较高 O(nkt)。
K-means算法缺点的改进:
1).针对上述缺点2),通过类的自动合并和分裂,得到较为合理的类型数目K,例如 ISODATA 算法。
2).针对上述缺点3),可选用二分K-均值聚类;或者多设置一些不同的初值,对比最后的运算结果,一直到结果趋于稳定结束。
3).针对上述缺点5),改成求点的中位数,这种聚类方式即K-Mediods聚类(K中值)。
k值如何确定
K-mediods(K中心点)算法
K-mediods算法是对K-means算法的一种改进算法。
K-mediods算法优点:
1).优点与K-means算法相同。
2).与K-means相比,K-mediods算法对于噪声不那么敏感,离群点就不会造成划分结果的偏差过大。
K-mediods算法缺点:
1).有K-means同样的缺点。如:必须事先确定类簇数和中心点,簇数和中心点的选择对结果影响很大;一般在获得一个局部最优的解后就停止;对于除数值型以外的数据不适用;只适用于聚类结果为凸形的数据集等。
2) K-mediods是对K-means的改进,但由于按照中心点选择的方式进行计算,算法的时间复杂度也比K-means上升了O(n)。
K-mediods算法描述:
1). 首先随机选取一组样本作为中心点集,每个中心点对应一个簇
2). 计算各样本点到各个中心点的距离(如欧几里德距离),将样本点放入距离中心点最近的那个簇中
3). 计算各簇中,距离簇内各样本点距离的绝度误差最小的点,作为新的中心点
4). 如果新的中心点集与原中心点集相同,算法终止;如果新的中心点集与原中心点集不完全相同,返回c)
K-mediods算法举例:
a) 设有(A,B,C,D,E,F)一组样本
b) 随机选择B、E为中心点
c) 计算D和F到B的距离最近,A和C到E的距离最近,则B,D,F为簇X1,A,C,E为簇X2
d) 计算X1发现,D作为中心点的绝对误差最小,X2中依然是E作为中心点绝对误差最小
e) 重新以D、E作为中心点,重复c)、d)步骤后,不再变换,则簇划分确定。
层次聚类
密度聚类
DSCAN
DSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)是一种基于密度的空间聚类算法。它将簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为簇,并在具有噪声的空间数据库中发现任意形状的聚类。
优点:可以对任何形状的数据进行聚类,而K-means系列主要针对高斯分布的数据,类圆形的数据。
函数解释:
sklearn.cluster.dbscan(X, eps=0.5, min_samples=5, metric=‘minkowski’, algorithm=‘auto’, leaf_size=30, p=2, sample_weight=None, random_state=None)
Parameters:
X:数组或稀疏矩阵,待聚类的特征数组。
eps:float,可选,阈值,指两个样本之间的最大距,在距离内则视为在同一个邻域中。
min_samples:int,可选,将某个点视为核心点的邻域中的样本数。
algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},可选最近邻模块用来计算点距离和寻找最近邻的算法。
leaf_size:int,可选(默认值=30)。作为BallTree或cKDTree的参数,影响构造和查询的速度,以及存储树所需的内存。
Returns:
labels:标签
参数选择:
- 半径:半径是最难指定的 ,大了圈住的点就多,簇的个数就少了;反之,簇的个数就多,这对我们最后的结果是有很大影响的。这个时候K距离可以帮助我们来设定半径r,也就是要找到突变点,比如:首先选中一个点,计算它和其他点之间的距离,从小到大排序, ( d 1 , d 2 , ⋯ , d n ) (d_{1},d_{2},\cdots,d_{n}) (d1,d2,⋯,dn),我们发现 d 3 d_{3} d3和 d 4 d_{4} d4之间的差异很大,于是认为前面的距离是比较合适的,那么就可以指定r半径的大小为0.13。这虽然是一个可取的方法,但确实很麻烦。
| 0.1 | 0.11 | 0.13 | 0.4 | 0.46 | 0.49 |
|---|---|---|---|---|---|
| d 1 d_{1} d1 | d 2 d_{2} d2 | d 3 d_{3} d3 | d 4 d_{4} d4 | d 5 d_{5} d5 | d 6 d_{6} d6 |
代码:
for i in range(2724):
item_third_ = item_third[i]
item_third_name_ = item_third_name[i]
dept_id_ = dept_id[i]
dept_name_ = dept_name[i]
# m
info_sql = "select m,dt from table where dept_id='"+ dept_id_ +"' and item_third='"+ item_third_ +"'"
info_df = spark.sql(info_sql)
info_df = info_df.sort(info_df.dt.asc())
info_list = info_df.collect()
m = [float(x['m']) for x in info_list]
dt = [x['dt'] for x in info_list]
dt_time = [datetime.datetime.strptime(x,"%Y-%m") for x in dt]
# average_sale_price
average_sale_price_sql = "select average_sale_price,dt from table where item_third='"+ item_third_ +"'"
average_sale_price_df = spark.sql(average_sale_price_sql)
average_sale_price_df = average_sale_price_df.sort(average_sale_price_df.dt.asc())
average_sale_price_list = average_sale_price_df.collect()
average_sale_price = [float(x['average_sale_price']) for x in average_sale_price_list]
dt_2 = [x['dt'] for x in average_sale_price_list]
dt_2_time = [datetime.datetime.strptime(x,"%Y-%m") for x in dt_2]
# draw image
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['savefig.dpi'] = 100
plt.rcParams['figure.dpi'] = 100
fig = plt.figure()
fig.set_size_inches(18.5, 10.5)
plt.title('%s_%s_%s_%s_m' %(dept_id_, dept_name_, item_third_, item_third_name_))
ax1 = fig.add_subplot(211)
plt.plot(dt_time, m)
plt.grid()
plt.xlabel('dt')
plt.ylabel('m')
ax2 = fig.add_subplot(212)
plt.plot(dt_2_time, average_sale_price)
plt.grid()
plt.xlabel('dt_2')
plt.ylabel('average_sale_price')
plt.title('average_sale_price')
dept_name_backup = dept_name_.replace('/','')
item_third_name_backup = item_third_name_.replace('/','')
plt.savefig('./nox/average_sale_price_2year/%s_%s.png'%(dept_name_backup, item_third_name_backup), dpi=150)
国外有一个特别有意思的网站:https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/
它可以把我们DBSCAN的迭代过程动态图画出来。
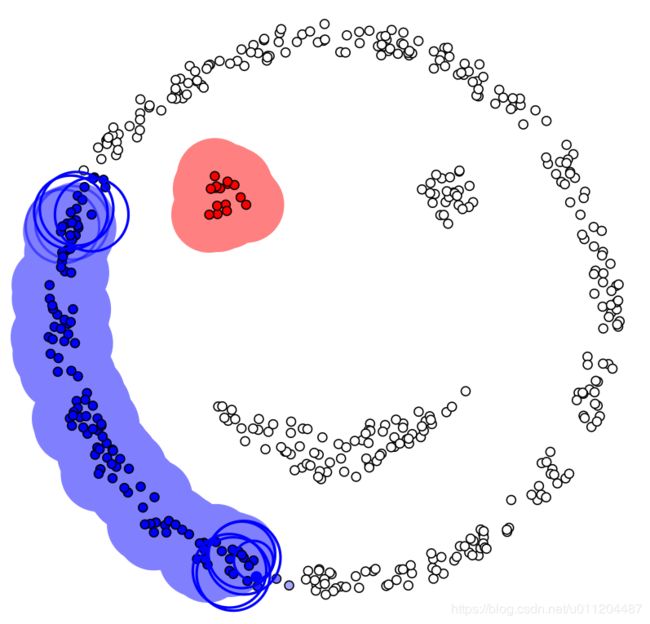
DBSCAN聚类的最终结果,如下:

没有颜色标注的就是圈不到的样本点,也就是离群点,DBSCAN聚类算法在检测离群点的任务上也有较好的效果。如果是传统的Kmeans聚类,我们也来看一下效果:

完美的体现出来DBSCAN算法基于密度聚类的优势。
谱聚类
常用的评估方法:轮廓系数(Silhouette)
s ( i ) = b ( i ) − a ( i ) m a x { b ( i ) , a ( i ) } s(i)=\frac{b(i)-a(i)}{max \left \{ b(i),a(i) \right \}} s(i)=max{b(i),a(i)}b(i)−a(i)
s ( i ) = { 1 − a ( i ) b ( i ) , a ( i ) < b ( i ) 0 , a ( i ) = b ( i ) a ( i ) b ( i ) − 1 , a ( i ) > b ( i ) s(i) = \left\{\begin{matrix} 1-\frac{a(i)}{b(i)},a(i)
计算样本i到同簇其它样本到平均距离ai。ai越小,说明样本i越应该被聚类到该簇,将ai称为样本i到簇内不相似度。
计算样本i到其它某簇Cj的所有样本的平均距离bij,称为样本i与簇Cj的不相似度。定义为样本i的簇间不相似度:bi=min(bi1,bi2,…,bik2)
si接近1,则说明样本i聚类合理
si接近-1,则说明样本i更应该分类到另外的簇
若si近似为0,则说明样本i在两个簇的边界上
所有样本的 s i s_{i} si的均值称为聚类结果的轮廓系数,是该聚类是否合理、有效的度量。
相似度度量及相互系数
相似度、距离计算
参考:
https://blog.csdn.net/luanpeng825485697/article/details/79443512
https://blog.csdn.net/huacha__/article/details/81094891