常见损失汇总
文章目录
- 回归模型的损失函数
- L1正则损失函数(即绝对值损失函数)
- L2正则损失函数(即欧拉损失函数)
- Pseudo-Huber 损失函数
- 分类模型的损失函数
- Hinge损失函数
- 两类交叉熵(Cross-entropy)损失函数
- 加权交叉熵损失函数
- Sigmoid交叉熵损失函数
- Softmax交叉熵损失函数
回归模型的损失函数
L1正则损失函数(即绝对值损失函数)
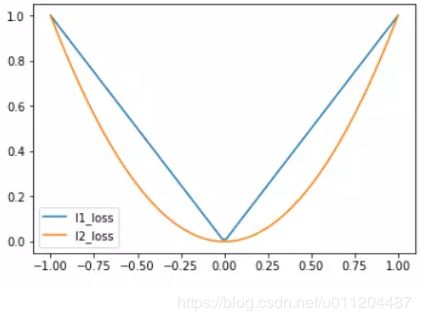
L1正则损失函数是对预测值与目标值的差值求绝对值,公式如下:
L ( Y , f ( X ) ) = ∣ Y − f ( X ) ∣ L(Y,f(X))=\left | Y-f(X) \right | L(Y,f(X))=∣Y−f(X)∣
缺点:L1正则损失函数在目标值附近不平滑,会导致模型不能很好地收敛。
L2正则损失函数(即欧拉损失函数)
L2正则损失函数是预测值与目标值差值的平方和,公式如下:
L ( Y , f ( X ) ) = ∑ i = 1 n ( Y − f ( X ) ) 2 L(Y,f(X))= \sum_{i=1}^{n} (Y-f(X))^{2} L(Y,f(X))=i=1∑n(Y−f(X))2
当对L2取平均值,就变成均方误差(MSE, mean squared error),公式如下:
M S E ( Y , f ( X ) ) = 1 n ∑ i = 1 n ( Y − f ( X ) ) 2 MSE(Y,f(X))= \frac{1}{n}\sum_{i=1}^{n} (Y-f(X))^{2} MSE(Y,f(X))=n1i=1∑n(Y−f(X))2
优点:L2正则损失函数在目标值附近有很好的曲度,离目标越近收敛越慢,是非常有用的损失函数。
L1、L2正则损失函数如下图所示:
Pseudo-Huber 损失函数
Huber损失函数经常用于回归问题,它是分段函数,公式如下:
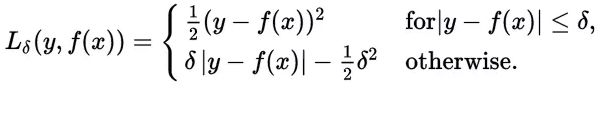
从这个公式可以看出当残差(预测值与目标值的差值,即y-f(x) )很小的时候,损失函数为L2范数,残差大的时候,为L1范数的线性函数。该公式依赖于参数delta,delta越大,则两边的线性部分越陡峭。
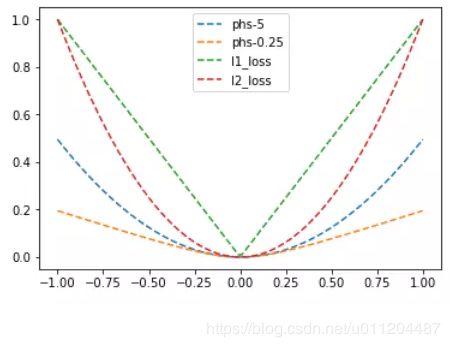
L1、L2、Huber损失函数的对比图如下,其中Huber的delta取0.25、5两个值:
分类模型的损失函数
Hinge损失函数
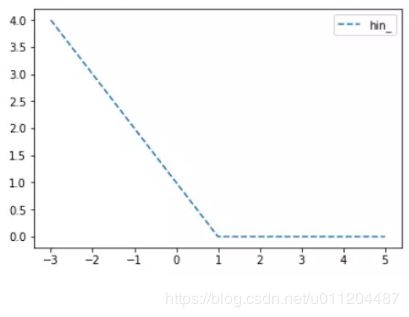
又名折页损失函数、铰链损失函数。Hinge损失常用于二分类问题,主要用来评估向量机算法(SVM),但有时也用来评估神经网络算法,公式如下:
L ( y ) = m a x ( 0 , 1 − t ⋅ y ) L(y)=max(0,1-t\cdot y) L(y)=max(0,1−t⋅y)
上面的代码中,目标值为1,当预测值离1越近,则损失函数越小,如下图:
两类交叉熵(Cross-entropy)损失函数
交叉熵来自于信息论,是分类问题中使用广泛的损失函数。交叉熵刻画了两个概率分布之间的距离,当两个概率分布越接近时,它们的交叉熵也就越小,给定两个概率分布p和q,则距离如下:
H ( p , q ) = − ∑ x p ( x ) l o g ( x ) H(p,q)=-\sum_{x}p(x)log(x) H(p,q)=−x∑p(x)log(x)
对于两类问题,当一个概率p=y,则另一个概率q=1-y,因此代入化简后的公式如下:
H ( p , q ) = − ∑ i p ( i ) l o g q ( i ) = − y l o g y ^ − ( 1 − y ) l o g ( 1 − y ^ ) H(p,q)=-\sum_{i}p(i)logq(i)=-ylog\widehat{y}-(1-y)log(1-\widehat{y}) H(p,q)=−i∑p(i)logq(i)=−ylogy −(1−y)log(1−y )
Cross-entropy损失函数主要应用在二分类问题上,预测值为概率值,取值范围为[0,1],损失函数图如下:

加权交叉熵损失函数
加权交叉熵损失函数是Sigmoid交叉熵损失函数的加权。
Sigmoid交叉熵损失函数
与上面的两类交叉熵类似,只是将预测值y_pred值通过sigmoid函数进行转换,再计算交叉熵损失。由于sigmoid函数会将输入值变小很多,从而平滑了预测值,使得sigmoid交叉熵在预测值离目标值比较远时,其损失的增长没有那么的陡峭。与两类交叉熵的比较图如下:
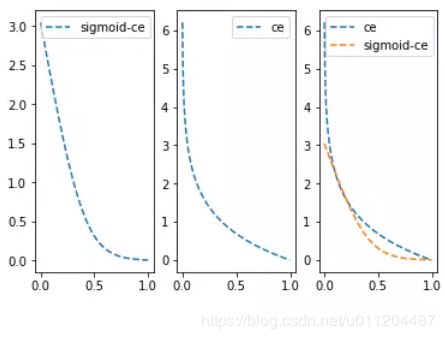
Softmax交叉熵损失函数
在Logistic regression二分类问题中,我们可以使用sigmoid函数将输入映射到区间中,从而得到属于某个类别的概率。将这个问题进行泛化,推广到多分类问题中,我们可以使用softmax函数,对输出的值归一化为概率值。通过softmax函数将输出结果转化成概率分布,从而便于输入到交叉熵里面进行计算(交叉熵要求输入为概率),softmax定义如下:
y ′ = s o f t m a x ( y i ) = e y i ∑ j = 1 n e y i {y}'=softmax(y_{i})=\frac{e^{y_{i}}}{\sum_{j=1}^{n}e^{y_{i}}} y′=softmax(yi)=∑j=1neyieyi
以上可以看出: ∑ y ′ = 1 \sum {y}'=1 ∑y′=1,这也是为什么softmax层的每个节点的输出值成为了概率和为1的概率分布。
Softmax+交叉熵也被称为Softmax损失函数,它表达式为:
H ( P , T ) = − ∑ 1 C P l o g ( T ) H(P,T)=-\sum_{1}^{C}Plog(T) H(P,T)=−1∑CPlog(T)
其中,P为样本的期望输出,它是一个one-hot编码形式。T为样本的实际输出,其中 T = [ s o f t m a x ( y 1 ) , s o f t m a x ( y 2 ) , . . . , s o f t m a x ( y i = n ) ] T=[softmax(y_{1}),softmax(y_{2}),...,softmax(y_{i=n})] T=[softmax(y1),softmax(y2),...,softmax(yi=n)]。这里P和T是一个长度与类别数相同的集合。
图见《百面机器学习》P143
总结:
| 损失 | 凸函数 | 光滑 | ||
|---|---|---|---|---|
| 绝对值损失 | 非凸 | 非光滑 | 回归 | |
| 欧拉损失 | 凸 | 光滑 | 回归 | |
| Pseudo-Huber 损失 | 回归 | |||
| Logistic损失 | 回归 | |||
| Hinge损失 | 非光滑 | 分类 | ||
| 0-1损失 | 非凸 | 非光滑 | 分类 | |
| 两类交叉熵损失 | 分类 | |||
| Sigmoid交叉熵损失 | 分类 | |||
| Softmax交叉熵损失 | 分类 |
在实际使用中,对于回归问题经常会使用MSE均方误差(L2取平均)计算损失,对于分类问题经常会使用Sigmoid交叉熵损失函数。
参考:
https://my.oschina.net/u/876354/blog/1940819
https://blog.csdn.net/lilong117194/article/details/81542667
https://blog.csdn.net/chaipp0607/article/details/73392175