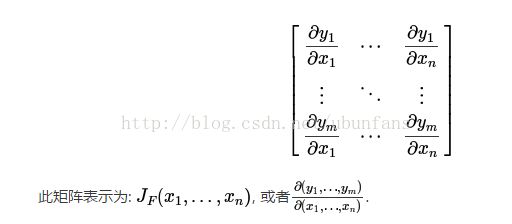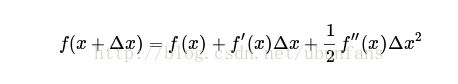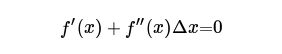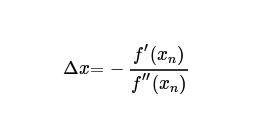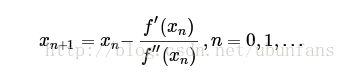机器学习的基础算法--牛顿法

牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。

把非线性函数  在  处展开成泰勒级数，取其线性部分，作为非线性方程的近似方程， 则有 

设  ，则其解为 

因为这是利用泰勒公式的一阶展开，  ，这里并不是完全相等，而是近似相等，即去掉泰勒级数2级以上的项，这里求得的  并不能让  ，只能说  的值比  更接近  ，于是乎，迭代求解的想法就很自然了，再把f(x)在x1 处展开为泰勒级数，取其线性部分为  的近似方程，若  ，则得  如此继续下去，得到牛顿法的迭代公式：

  ，通过迭代，这个式子必然在  的时候收敛。上述过程可以用一张动图来体现：

那么牛顿法对比于梯度下降有什么优势了？不难发现牛顿法是二阶收敛，收敛速度明显要高于梯度下降法。举个很简单的例子，梯度下降是考虑下山的坡度最陡，而牛顿法则是不仅要考虑下坡陡，还要考虑下坡变化的速率更快。

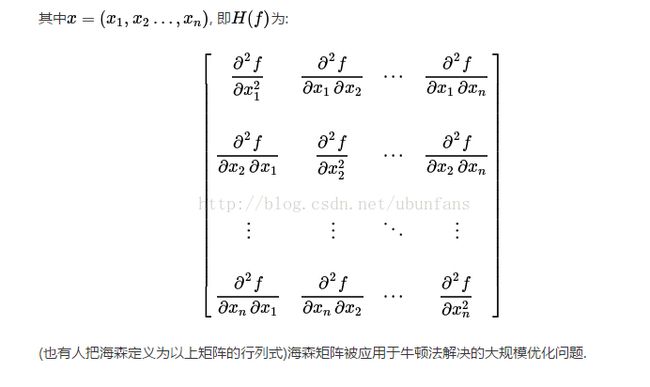
牛顿法主要可以解决两个问题，第一个是求根问题，比如一个一元五次方程的根，我们用代数的方法是求不出解的（阿贝尔和伽罗瓦的工作证明了一般一元五次方程没有根式解），而我们可以用牛顿法通过计算机来逼近对应的根；另外一个问题就是最优化的问题，这也是机器学习中和梯度下降法使用频率相当的一种优化算法。这里有几个常用的矩阵，是针对多元函数的问题，即雅克比矩阵和海森矩阵。简单介绍一下二者，雅克比矩阵为函数对各自变量的一阶导数，海森矩阵为函数对自变量的二次微分。形式分别如下：

要想实现多元函数的优化问题，必须使用这两个矩阵进行计算。

牛顿法利用计算机实现的整体思路：

求解最优化问题，一般是求解极大值或者极小值的问题，即目标函数导数求零点的问题，f' = 0;

把f(x)用泰勒公式展开到二阶，即：

等号左边和f(x)近似相等，抵消。然后对求导，得到：

                                                                          

更进一步：

                                                                                

然后得到迭代式子：

推广到多元函数，应用雅克比矩阵和海森矩阵，则有：

1、先决条件

暂无先决条件。

2、算法参数的初始化

这里我们需要初始化一些变量，比如epsilon（阈值），迭代次数N，变量初始值x0，y0……

3、算法的过程：这一步很重要，这里是变量更新的重要步骤；

1、确定对应的目标函数，并对目标函数进行优化，求解最有解，f（x0，x1，......)

2、对目标函数分别求解一阶偏导数和二阶偏导数，分别构建雅克比矩阵和海森矩阵，并用海森矩阵的逆左乘，雅克比矩阵右乘变量，即得到变化度量值。

3、确定迭代次数和变化度量值小于阈值epsilon，此时算法终止，而变量也会停止更新，形成最优参数，否则，进入步骤4.

以下是用python实现二元函数求解最优化值的code；

import numpy as np
def newton_method(x0,y0,N,E):
	X1,X2,Y,Y_d=[],[],[],[]#X1,X2为二元函数的两个特征，Y为标签，Y_d为
	n=1#迭代次数记录
	X1.append(x0)
	X2.append(y0)
	Y.append(f(x0,y0))#算法过程第一步，确定目标函数f(x0,y0)，对它进行参数优化
	ee=g(x0,y0)#初始化阈值
	e=(ee[0,0]**2+ee[1,0]**2)**0.5#二元函数求解的一阶导数为一个2*1维的雅克比矩阵，一种刻画变化的函数
	#算法迭代过程
	while nE:
		n+=1
		#迭代两个变量
		X=-np.dot(np.linalg.inv(G(x0,y0)),g(x0,y0))
		x0+=X[0,0]
		y0+=X[1,0]
		ee=g(x0,y0)
		e=(ee[0,0]**2+ee[1,0]**2)**0.5#更新阈值
		print(n)
	print (x0,y0,N,E)
f=lambda x,y:3*x**2+3*y**2-x**2*y#声明目标函数
g=lambda x,y:np.array([[6*x-2*x*y],[6*y-x**2]])#构建目标函数的雅克比矩阵
G=lambda x,y:np.array([[6-2*y,-2*x],[-2*x,6]])#构建目标函数的海森矩阵
x0,y0,N,E=-2,4,10,10**(-6)
newton_method(x0,y0,N,E)

out：

2
3
4
5
6
-4.242640687119334 3.0000000000000355 10 1e-06

在这里我还没有弄懂变化度量的取值，这也是仿照网络上某位大神的code写的，主要为了校核一下算法是否正确，好吧，这是目前我碰到最难的算法，不借助numpy包，我都不知道该怎么求海森矩阵的逆。