大话数据结构学习笔记 - 图的最小生成树之Prim算法

大话数据结构学习笔记 - 图的最小生成树之Prim算法

最小生成树(Minimum Cost Spanning Tree) 即构造连通图的最小代价生成树

Prim算法

基本思想

对于图G而言，V是所有顶点的集合。现在设置两个新的集合U和T， 其中U用于存放G的最小生成树中的顶点，T存放G的最小生成树中的边。从所有 u∈U,v∈(V−U) u ∈ U , v ∈ ( V − U ) )( V−U V − U 表示除去U的所有顶点)的边中选取权值最小的边(u, v)， 将顶点v加入集合U中，将边(u, v)加入集合T中，如此不断重复，知道U = V为止，最小生成树构造完毕，这是集合T中包含了最小生成树的所有边。

Prim算法图解

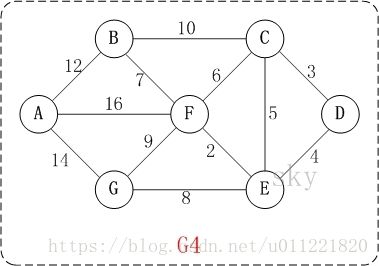
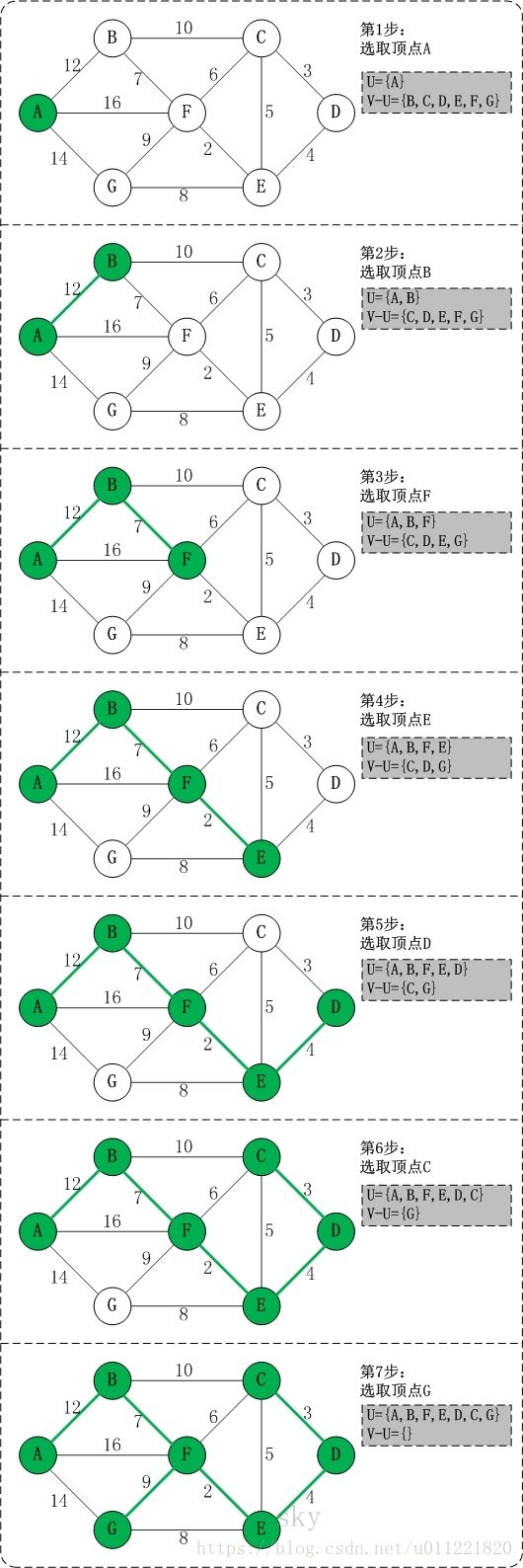
以上图G4为例，对Prim算法进行模拟演示（假定选择A顶点为起始点）

初始状态： V是所有顶点集合，即 V={A,B,C,D,E,F,G} V = { A , B , C , D , E , F , G }

第一步：A为起始点，将A加入到顶点集合U中， U={A},V−U={B,C,D,E,F,G} U = { A } , V − U = { B , C , D , E , F , G }

第二步：从U集合所有顶点的边集中，遍历到(A, B)的权值最小，故将B加入到顶点集合U中， U={A,B},V−U={C,D,E,F,G} U = { A , B } , V − U = { C , D , E , F , G }

第三步：从U集合所有顶点的边集中，遍历到(B, F)的权值最小，故将F加入到顶点集合U中， U={A,B,F},V−U={C,D,E,G} U = { A , B , F } , V − U = { C , D , E , G }

第四步：从U集合所有顶点的边集中，遍历到(F, E)的权值最小，故将E加入到顶点集合U中， U={A,B,F,E},V−U={C,D,G} U = { A , B , F , E } , V − U = { C , D , G }

第五步：从U集合所有顶点的边集中，遍历到(E, D)的权值最小，故将D加入到顶点集合U中， U={A,B,F,E,D},V−U={C,G} U = { A , B , F , E , D } , V − U = { C , G }

第六步：从U集合所有顶点的边集中，遍历到(D, C)的权值最小，故将C加入到顶点集合U中， U={A,B,F,E,D,C},V−U={G} U = { A , B , F , E , D , C } , V − U = { G }

第七步：从U集合所有顶点的边集中，遍历到(F, G)的权值最小，故将G加入到顶点集合U中， U={A,B,F,E,D,C,G},V−U={} U = { A , B , F , E , D , C , G } , V − U = { } , 此时 U=V U = V

此时，最小生成树构造完成，其顶点依次为A, B, F, E, D, C, G

代码

邻接矩阵结构

以邻接矩阵为例

#define MAXVER 10
typedef char VertexType;

typedef struct 
{
    VertexType vexs[MAXVER];
    int arc[MAXVER][MAXVER];
    int numVertexes, numEdges;
}MGraph;

Prim算法

/* Prim 算法生成最小生成树 */
void MiniSpanTree_Prim(MGraph G)
{
    int min, i, j, k;  // min 为当前权值最小值
    int lowcost[MAXVEX];  /* 保存顶点间边的权值 */
    int adjvex[MAXVEX];   /* 保存相关顶点的下标，即下标与其值所连边为当前最小权值边 */
    lowcost[0] = 0;  /* 选取第一个顶点为起始点， 即 v0 加入树， lowcost的值为0，在这里就是此下标的顶点已经加入生成树 */
    adjvex[0] = 0;   /* 初始化第一个顶点下标为0 */
    for(i = 1; i < G.numVertexes; i++)  /* 循环除下标为 0 外的全部顶点 */
    {
        lowcost[i] = G.arc[0][i];  /* 将与 v0 顶点有边的权值存入数组 */
        adjvex[i] = 0;  /* 将其他所有顶点的值初始化为 v0 的下标 */
    }
    for(i = 1; i < G.numVertexes; i++)
    {
        min = INF;   /* 初始化最小权值为 无穷大 */
        j = 1, k = 0;
        while(j < G.numVertexes)  /* 循环全部顶点，寻找当前最小生成树顶点集合中最小权值的边 */
        {
            if(lowcost[j] != 0 && lowcost[j] < min)  /* 如果权值不为 0(即不在树中), 且权值小于 min */
            {
                min = lowcost[j];  /* 则让当前权值成为最小值 */
                k = j;             /* 将当前最小值的下标存入k */
            }
            j++;
        }
        lowcost[k] = 0;  /* 将当前顶点的权值设置为0, 表示此顶点已加入树的顶点集合 */
        printf("(%d, %d)", adjvex[k], k);  /* 打印当前顶点边中权值最小的边 */
        for(j = 1; j < G.numVertexes; j++)  /* 循环所有顶点 */
        {
            /* 如果下标为 k 的顶点边集中权值小于已存在的权值, 比如 (v0, v6)权值为INF, 而(v1, v6)权值为 16， 更新*/
            if(lowcost[j] != 0 && G.arc[k][j] < lowcost[j])
            {
                lowcost[j] = G.arc[k][j];  /* 将较小的权值存入 lowcost 相应位置 */
                adjvex[j] = k;   /* 将下标为 k 的顶点存入 adjvex */
            }
        }
    }
}

算法源码

邻接矩阵Prim算法源码

结语

下篇博客会更新最小生成树的Kruskal算法