《剑指offer》刷题笔记（栈和队列）：滑动窗口的最大值

《剑指offer》刷题笔记（栈和队列）：滑动窗口的最大值

---

• 转载请注明作者和出处：http://blog.csdn.net/u011475210
• 代码地址：https://github.com/WordZzzz/Note/tree/master/AtOffer
• 刷题平台：https://www.nowcoder.com/
• 题  库：剑指offer
• 编  者：WordZzzz

---

题目描述

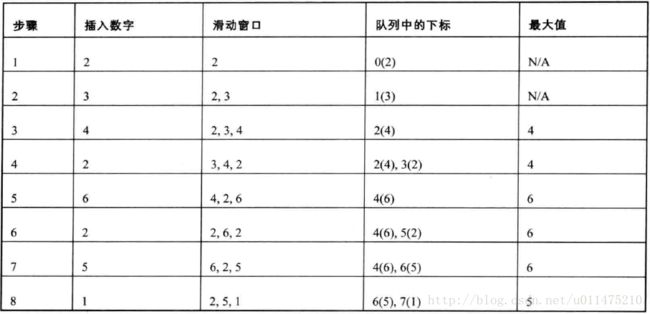
给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。

解题思路

实际上一个滑动窗口可以看成是一个队列。当窗口滑动时，处于窗口的第一个数字被删除，同时在窗口的末尾添加一个新的数字。这符合队列的先进先出特性。那么剩下的任务就是如何从队列中找出它的最大值了。

之前有题目是用O(1)时间得到最小值的栈，也有题目是用两个栈实现队列，如果结合起来，我们就会很容易写出来代码。总的时间复杂度为O(n)。

但是在这里，我们并不打算用上述方法，因为这相当于要写两个题的代码。我们试想一下，如果把比大小这一步放在入栈之前，情况会不会好点？

我们可以用STL中的deque来实现，接下来我们以数组{2,3,4,2,6,2,5,1}为例，来细说整体思路。

数组的第一个数字是2，把它存入队列中。第二个数字是3，比2大，所以2不可能是滑动窗口中的最大值，因此把2从队列里删除，再把3存入队列中。第三个数字是4，比3大，同样的删3存4。此时滑动窗口中已经有3个数字，而它的最大值4位于队列的头部。

第四个数字2比4小，但是当4滑出之后它还是有可能成为最大值的，所以我们把2存入队列的尾部。下一个数字是6，比4和2都大，删4和2，存6。就这样依次进行，最大值永远位于队列的头部。

但是我们怎样判断滑动窗口是否包括一个数字？应该在队列里存入数字在数组里的下标，而不是数值。当一个数字的下标与当前处理的数字的下标之差大于或者相等于滑动窗口大小时，这个数字已经从窗口中滑出，可以从队列中删除。

下述代码中，index是一个两端开口的队列，用来保存有可能是滑窗最大值的数字的下标。在存入一个数字的下标之前，首先要判断队列里已有数字是否小于待存入的数字。如果已有的数字小于待存入的数字，这些数字已经不可能是滑动窗口的最大值，因此它们将会依次从队列的尾部删除（调用pop_back）。同时，如果队列头部的数字已经从窗口里滑出，滑出的数字也需要从队列的头部删除（调用pop_front）。由于队列的头部和尾部都有可能删除数字，这也是需要两段开口的队列的原因。

C++版代码实现

class Solution {
public:
    vector<int> maxInWindows(const vector<int>& num, unsigned int size)
    {
        vector<int> maxInWindows;
        if(num.size() >= size && size >= 1){
            deque<int> index;
            for(unsigned int i = 0; i < size; ++i){
                while(!index.empty() && num[i] >= num[index.back()])
                    index.pop_back();
                index.push_back(i);
            }
            for(unsigned int i = size; i < num.size(); ++i){
                maxInWindows.push_back(num[index.front()]);
                while(!index.empty() && num[i] >= num[index.back()])
                    index.pop_back();
                if(!index.empty() && index.front() <= (int)(i-size))
                    index.pop_front();
                index.push_back(i);
            }
            maxInWindows.push_back(num[index.front()]);
        }
        return maxInWindows;
    }
};

系列教程持续发布中，欢迎订阅、关注、收藏、评论、点赞哦～～(￣▽￣～)～

完的汪(∪｡∪)｡｡｡zzz