二叉树原理及实现
完整代码在这里 https://github.com/zhangjunapk/half_search_tree
树被广泛使用,比如文件系统,unix上用到了红黑树,windows上用到了树
二分查找树可以说是一个有序的集合,节点之间用链表链接起来,可以用二分搜索的方式来对搜索
二分查找树在写入上做了一个性能的权衡,每次写入数据都要遍历,然后放到合适的位置
是一种很平衡的数据存储结构
先看看百度百科对二分搜索树的定义把
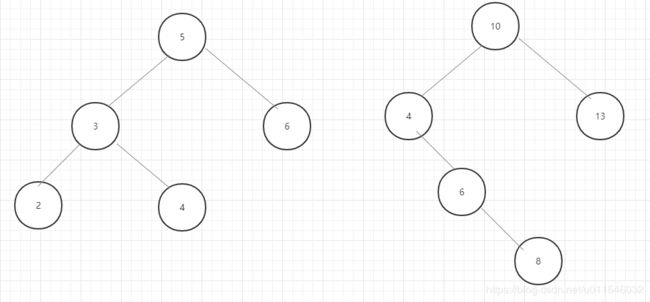
只要满足这些条件的树都能被称为二分查找树
比如可以是这样子
接下来我们看看为什么二分查找树为什么快
如果我们仅仅用链表的话,需要遍历所有节点,直到找到值
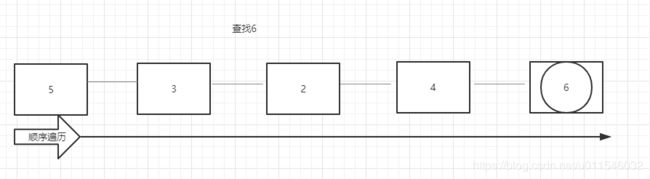
加入我们查找6
传统链表就需要顺序遍历节点,直到找到对应的值
但是二分搜索树就不同了,在插入的时候就是排序好的,查找的话直接搜索就行了
在搜索的时候,会判断当前数值是否一致,然后把要搜索的数值和当前节点进行大小对比,如果大于当前,那就从左边继续递归遍历(左边没有就结束),右边也是一样,这样就实现了二分查找(二分查找有序数组也有和当前节点对比的逻辑,然后切换索引),二分查找树比数组方便的地方就是不用再进行一次排序了,因为插入的时候就保证了顺序性。当然这是有代价的,那就是插入的时候没有数组性能高
接下来看插入代码的逻辑
public void insert(String k,Integer v){
//先判断root是否为空
if(root==null){
root=new Node(k,v);
System.out.println("直接插到根 ");
return;
}
//接下来遍历节点
Node node = new Node(k, v);
forInsert(node,root);
System.out.println("--------------------------------");
}先看根节点是否为空,如果为空就直接初始化根节点,不然执行递归插入
//递归遍历,然后插入数值
private int forInsert(Node insertNode, Node node) {
//百度百科上说键值不能相等
if(insertNode.getVal().equals(node.getVal()))
return -1;
//判断都空的
if(node.getLeft()==null&&node.getRight()==null){
System.out.println("两边都空");
//判断这个数值和当前节点的大小
if(insertNode.getVal()<=node.getVal()){
System.out.println(" 插入到"+node.getVal()+"的左边"+insertNode.getVal());
node.setLeft(insertNode);
return 0;
}
if(insertNode.getVal()>=node.getVal()){
System.out.println(" 插入到右边");
node.setRight(insertNode);
return 0;
}
}
//判断要插入的值是否比当前的节点大
if(insertNode.getVal()<=node.getVal()){
if(node.getLeft()!=null){
return forInsert(insertNode,node.getLeft());
}
//不然直接insert
node.setLeft(insertNode);
return 0;
}
if(insertNode.getVal()>=node.getVal()){
if(node.getRight()!=null){
return forInsert(insertNode,node.getRight());
}
//不然直接insert
node.setRight(insertNode);
return 0;
}
return -1;
}先判断左右是否都为空,为空就把要插入的数值和当前的节点进行对比,然后直接set进去
然后就递归插入,进入下一层,然后接着判断,直到左右都为空,就接着判断大小,然后set进去
数据插入进去了,我们就需要拿出来,这里我写了三种遍历方式
1.先序遍历(深度优先)
2.后序遍历(深度优先)
3.按层遍历(广度优先)
先看广度优先的
//按层遍历
public void eachLayer(){
System.out.println(root.getVal());
layEach(root);
}
这里先输出根节点
然后调用递归遍历层的方法
//广度优先(按层遍历里面的递归)
private void layEach(Node node) {
if(node.getLeft()!=null){
System.out.println("L "+node.getLeft().getVal());
}
if(node.getRight()!=null){
System.out.println("R "+node.getRight().getVal());
}
if(node.getLeft()!=null){
layEach(node.getLeft());
}
if(node.getRight()!=null){
layEach(node.getRight());
}
}这里直接判断是否为空,然后直接打印
这里我这样写是有原因的,因为需要一层一层打印,所有就先输出,然后进入下一层递归
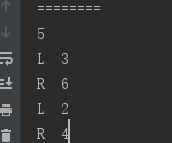
这就是调用层级遍历的输出
然后是先序遍历
//递归先序遍历
private void eachBefore(Node node) {
System.out.println(node.getVal());
if(node.getLeft()!=null)
eachBefore(node.getLeft());
if(node.getRight()!=null)
eachBefore(node.getRight());
}
先序遍历是从根节点开始遍历,然后依次遍历到左子树的叶,然后才会遍历右子树(层级调用真好玩)
接下来是后序遍历
//递归后序遍历
private void eachAfter(Node node) {
System.out.println(node.getVal());
if(node.getRight()!=null)
eachBefore(node.getRight());
if(node.getLeft()!=null)
eachBefore(node.getLeft());
}
这里把先序遍历换一下就行了,先遍历右子树,再遍历左子树
这是完整代码 https://github.com/zhangjunapk/half_search_tree