ACM-矩阵之递推式

有时候我们需要求一个数列的某一项，当然这时候自然会想到能不能求取这个数列的通项公式，这里我总结了一下，通项公式有两种，一种是只与项数有关的，即要求第n项，直接将n带入通项计算即可，另外一种是与某一项具体的值有关的，即要求第n项，需要已知另外不定的某一项或几项的值。比如等差数列属于第一种，Fibonacci数列属于第二种。当然，第一种数列没啥说的，已知通项求任意一项都能在O（1）的时间内搞定。第二种就没有那么幸运了，我们发现其实它的通项其实就是递推式，那么意味着当我们需要求某一项时，必须由某一项慢慢递推着走，毫无疑问，如果要求的项数很大，那么递推的次数可能也就很多，结果就只能是超时了。那有没有方法突破这种限制呢？答案就是矩阵。怎么去做呢？关键是要利用这一类通项所具有的递推性质，递推其实就是迭代的过程，刚好矩阵也有迭代的运算，那就是幂次（自身不断迭代），试想如果我们可以利用矩阵的幂运算来代替通项公式的递推，那么我们就可以利用前面学过的快速幂算法来优化、加速运算的过程。于是，最为关键的问题就来了，即如何找出这样一个合适的矩阵呢？其实，构造这样一个矩阵仅仅需要从我们的递推式出发，其它的并没固定方法，然后目的就是需要一个矩阵，它可以经过多次幂运算后，乘上初始矩阵后可以表示任意的某一项，这一项可以存在于最终矩阵的任何一个位置，只要可以提取出来就行。

说了这么多，感觉也很抽象，那下面就拿一道例题来具体分析，HDOJ：1588，时空转移（点击打开链接），题目如下：

Gauss Fibonacci

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2361    Accepted Submission(s): 991

Problem Description

Without expecting, Angel replied quickly.She says: "I'v heard that you'r a very clever boy. So if you wanna me be your GF, you should solve the problem called GF~. "
How good an opportunity that Gardon can not give up! The "Problem GF" told by Angel is actually "Gauss Fibonacci".
As we know ,Gauss is the famous mathematician who worked out the sum from 1 to 100 very quickly, and Fibonacci is the crazy man who invented some numbers.

Arithmetic progression:
g(i)=k*i+b;
We assume k and b are both non-nagetive integers.

Fibonacci Numbers:
f(0)=0
f(1)=1
f(n)=f(n-1)+f(n-2) (n>=2)

The Gauss Fibonacci problem is described as follows:
Given k,b,n ,calculate the sum of every f(g(i)) for 0<=i The answer may be very large, so you should divide this answer by M and just output the remainder instead.

 

Input

The input contains serveral lines. For each line there are four non-nagetive integers: k,b,n,M
Each of them will not exceed 1,000,000,000.

 

Output

For each line input, out the value described above.

 

Sample Input

2 1 4 100 2 0 4 100

 

Sample Output

21 12

 

题意：

给出k，b，n（0<=i

分析：

看到数据的范围，我们就应该想到普通的暴力是不可取的，所以这道题需要解决两个问题，一个是如何快速的计算Fibonacci数列的第g（i）项，二是如何快速的将它们相加求和。

首先来解决第一个问题，本文的主题不就是快速的计算递推式的任意一项吗？所以，先让我们来找找前面的提到过的构造矩阵，从数列的递推式出发：f（n）= f（n-1）+ f（n-2），我们换一个简洁一些的等式：c = a + b（c是本项，a是后第一项，b是后第二项）。很明显，我们最后所得到的矩阵中必须要包含a+b一项，因为这正是我们想要计算的，同时我们的初始矩阵也不难想到，必须要有a和b，这样才能得到下一项c，那么关键就是构造矩阵了，其实反推一下就可以了，具体看的图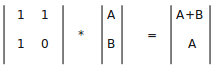：。如此一来只需要将上面第一个矩阵开i次幂，然后乘上第二个矩阵，就可以得到包含Fibonacci数列第i项的第三个矩阵了，其中a=0，b=1。

接下来需要解决第二个问题，由于g（i）= k*i + b的，所以题目要求计算的就是f（b）+ f（k+b）+ f（k*2+b）+ ... + f（k*（n-1）+b），依据上面的构造矩阵，我们用矩阵A重写前面的等式，即：A^b+ A^(k+b）+ A^（k*2+b）+ ... + A^（k*（n-1）+b），继续变形：A^b*(1+ A^k+ A^（k*2）+ ... + A^（k*（n-1）)，令矩阵B=A^k，那么A^b*(1+ B ^1+ B^2）+ ... + B^（n-1）），结果已经很明显了，还记得二分吗？括号里面的和不正是上一次我们写过的二分求和么。到此，结果就可以快速的计算出来了。

源代码：

#include 
#include 

#define LL __int64
const int MAXN = 10;
int MOD;
struct Mat
{
    int n, m;
    LL mat[MAXN][MAXN];
    Mat()
    {
        memset(mat, 0, sizeof(mat));
        n = m = MAXN;
    };
    void init()                                       // 初始化为单位矩阵
    {
        for(int i=1; i<=n; ++i)
            for(int j=1; j<=m; ++j)
                mat[i][j] = (i==j);
    }
    Mat operator * (Mat b)                            // 重载乘法
    {
        Mat c;
        c = Mat();
        c.n = n;
        c.m = b.m;
        for(int i=1; i<=n; ++i)                       // 注意这里从1开始
            for(int j=1; j<=b.m; ++j)
            {
                //if(mat[j][i] <= 0)  continue;       // 剪枝
                for(int k=1; k<=m; ++k)
                {
                    //if(b.mat[i][k] <= 0) continue;  // 剪枝
                    c.mat[i][j] += (mat[i][k]*b.mat[k][j]) % MOD;
                    c.mat[i][j] %= MOD;
                }
            }
        return c;
    }
    Mat operator + (Mat b)                            // 重载加法
    {
        Mat c;
        c.n = n;
        c.m = m;
        for(int i=1; i<=n; ++i)
            for(int j=1; j<=m; ++j)
                c.mat[i][j] = (mat[i][j]+b.mat[i][j]) % MOD;
        return c;
    }
    Mat pow(Mat a, int k)                             // 快速幂
    {
        Mat c;
        c.n = a.n;
        c.m = a.n;
        for(int i=1; i<=a.n; ++i)                     // 初始化为单位矩阵
            c.mat[i][i] = 1;
        while(k)
        {
            if(k & 1)
                c = c*a;
            a = a*a;
            k >>= 1;
        }
        return c;
    }
};

Mat tmp;
Mat slove(Mat init, int k)
{
	if(k == 1)
		return init;
	tmp = slove(init, k>>1);                      // 递归二分求解
    tmp = tmp + tmp * init.pow(init,k>>1);
	if(k & 1)
		return tmp + init.pow(init,k);
	else
		return tmp;
}

int main()
{//freopen("sample.txt", "r", stdin);
    int k, b, n;
    while(~scanf("%d%d%d%d", &k, &b, &n, &MOD))
    {
        tmp.n = tmp.m = 2;
        Mat data;                                     // 构造矩阵
        data.n = data.m = 2;
        data.mat[1][2] = data.mat[2][1] = data.mat[2][2] = 1;
        data.mat[1][1] = 0;
        Mat base;                                     // 初始矩阵
        base.n = base.m = 2;
        base.mat[1][1] = base.mat[1][2] = base.mat[2][2] = 0;
        base.mat[2][1] = 1;
        Mat cyc;
        cyc.n = cyc.m = 2;
        cyc = cyc.pow(data, b);
        data = data.pow(data, k);
        Mat sig;                                      // 单位矩阵
        sig.n = sig.m = 2;
        sig.init();
        data = sig + slove(data,n-1);                 // B=A^k,1+B^1+B^2……+B^n-1
        data = cyc * data ;
        printf("%I64d\n", data.mat[1][2]);
    }
    return 0;
}

就这道题的构造矩阵来说，它还是属于比较简单的一种，如果问题比较复杂，那么有可能构造矩阵会变成神构造，一般人根本想不到，所以还是需要平时的积累，有了灵感就会少了很多麻烦。其它类似的题目还有，HDOJ：1757、2604、4291，POJ：3037、3735、3150。

好了，矩阵加速递推式的求解就说到这里了，下一文章我们将讨论矩阵在置换中的应用，传送门（点击打开链接）。