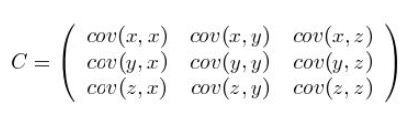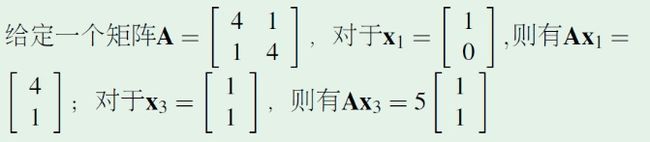最通俗易懂的PCA主成分分析推导
转载请注明出处,原文地址:
https://terrifyzhao.github.io/2018/06/30/PCA%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90.html
前言
说到PCA你是不是第一时间想到的是对协方差矩阵做特征值分解,但是为什么这么做呢?之前看过的大部分PCA博文也都是只简单介绍了PCA的流程,对其中的推导过程与原理并没有详细介绍,这篇文章的目的是从数学的角度,手推PCA每一个步骤,帮助读者了解PCA的工作机制是什么。文中的某些数学公式,可能会对某些读者产生不适,我会尽可能的用白话把其中原理讲解的通俗易懂。
PCA简介
PCA(Principal Component Analysis)是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降维。通俗讲就是将高维度数据变为低维度。例如基于电商的用户数据可能有上亿维,我们可以采用PCA把维度从亿级别降低到万级别或千级别,从而提高计算效率。
向量的内积
在开始下面的内容之前,我们需要弄懂几个基本概念,首相是向量的内积。
向量的内积我们在高中就已经学过,两个维数相同的向量的内积被定义为:
( a 1 , a 2 , . . . , a n ) ⋅ ( b 1 , b 2 , . . . b n ) T = a 1 b 1 + a 2 b 2 + . . . + a n b n (a_1,a_2,...,a_n)·(b_1,b_2,...b_n)^T = a_1b_1+a_2b_2+...+a_nb_n (a1,a2,...,an)⋅(b1,b2,...bn)T=a1b1+a2b2+...+anbn
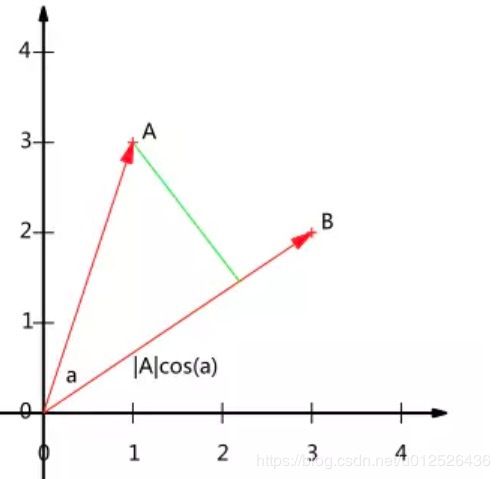
这个定义很好理解,那么内积的几何意义是什么呢,我们看个图
内积的另一种我们熟悉的表述方法为向量的模乘上向量之间的夹角的余弦值,即:
A ⋅ B = ∣ A ∣ ∣ B ∣ c o s ( a ) A·B=|A||B|cos(a) A⋅B=∣A∣∣B∣cos(a)
如果我们假设B的模为1,即单位向量,那么:
A ⋅ B = ∣ A ∣ c o s ( a ) A·B=|A|cos(a) A⋅B=∣A∣cos(a)
这里我们可以发现,内积其实就是A向量在B向量的方向上的投影的长度。
散度
接下来我们考虑一个问题:对于空间中的所有样本点,如何找到一个超平面对所有的样本进行恰当的表达?举个例子,例如我们在二维空间内,想把数据降为一维,那么应该把样本点投影到x轴还是y轴呢?
对于这个问题,我们需要找到的超平面需满足最大可分性:样本点在这个超平面上的投影能尽可能分开,这个分开的程度我们称之为散度,散度可以采用方差或协方差来衡量(在机器学中,样本的方差较大时,对最终的结果影响会优于方差较小的样本)如图,对于方差0.2的超平面散度高于方差为0.045的超平面,因此0.2方差的超平面即为我们需要的。
这里我们再简单补充下协方差的知识:
方差是用来形容单个维度的样本的波动程度,协方差是指多个维度的样本数据的相关性,其计算公式为:
C o v ( X , Y ) = ∑ i = 1 n ( X i − X ‾ ) ( Y i − Y ‾ ) ( n − 1 ) Cov(X,Y) = \frac{\sum_{i=1}^n(X_i- \overline X)(Y_i- \overline Y)}{(n-1)} Cov(X,Y)=(n−1)∑i=1n(Xi−X)(Yi−Y)
其中 C o v ( X , Y ) ∈ ( − 1 , 1 ) Cov(X,Y)\in (-1,1) Cov(X,Y)∈(−1,1),绝对值越大说明相关性越高。注意,协方差不等于相关系数,相关系数是协方差除标准差,相关系数的相除操作把样本的单位去除了,因此结果更加标准化一些,实际含义类似。
协方差矩阵
PCA的首要目标是让投影后的散度最大,因此我们要对所有的超平面的投影都做一次散度的计算,并找到最大散度的超平面。为了方便计算我们需要构建协方差矩阵。
图中是一个三维的协方差矩阵,其中对角线是样本本身的协方差即方差,非对角线是不同样本之间的协方差。
注意,在PCA中,我们会对所有的数据进行中心化的操作,中心化后数据的均值为0,即:
x i = x i − 1 m ∑ i = 1 m x i x_i = x_i - \frac{1}{m} \sum_{i=1}^mx_i xi=xi−m1i=1∑mxi
根据我们上文提到的协方差计算公式,我们可以得到数据样本的协方差矩阵为:
C o v ( X i ) = 1 m ∑ i = 1 m ( X i − X ‾ i ) 2 = 1 m ∑ i = 1 m ( X i ) 2 = 1 m ∑ i = 1 m X i ⋅ X i T \begin{aligned} Cov(X_i) &= \frac{1}{m} \sum_{i=1}^m (X_i-\overline X_i)^2\\ &= \frac{1}{m} \sum_{i=1}^m (X_i)^2\\ &= \frac{1}{m} \sum_{i=1}^m X_i·X_i^T\\ \end{aligned} Cov(Xi)=m1i=1∑m(Xi−Xi)2=m1i=1∑m(Xi)2=m1i=1∑mXi⋅XiT
我们设可投影的超平面为 V V V,我们要求投影的协方差,是不是可以根据我们第一条提到的向量的内积呢?因此我们可以得到投影后的值为 V T ⋅ X i V^T ·X_i VT⋅Xi,我们把投影后的方差计算一下
S 2 = 1 m ∑ i = 1 m ( V T X i − E ( V T X ) ) 2 S^2 = \frac{1}{m} \sum_{i=1}^m (V^T X_i-E(V^T X))^2 S2=m1i=1∑m(VTXi−E(VTX))2
这里我们进一步的做中心化操作,因此期望值为0,所以有:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ S^2 &= \frac{1…
仔细看,投影的方差即是原数据样本的协方差矩阵乘 V V T V V^T VVT。为了后续表述方便,我们设原数据样本的协方差矩阵为C,即:
S 2 = V T C V S^2 = V^TCV S2=VTCV
最大化散度
到了这一步,我们获得了投影的散度的计算方法。我们再看下PCA的首要目标:让投影后的散度最大,既然是要最大化散度,那么就会涉及到我们熟悉的优化问题了,不过这里有一个限制条件,即超平面向量的模为1即:
a r g m a x V T C V s . t . ∣ V ∣ = 1 \begin{aligned} argmax\ V^TCV\\ s.t.|V|=1\\ \end{aligned} argmax VTCVs.t.∣V∣=1
对于有限制条件的优化问题,我们采用拉格朗日乘子法来解决,即:
f ( V , α ) = V T C V − α ( V V T − 1 ) f(V,\alpha) = V^TCV -\alpha(VV^T-1) f(V,α)=VTCV−α(VVT−1)
对于求极值的问题,当然是求导啦,这里我们对V求导,即:
α f α v = 2 C V − 2 α V \frac{\alpha f}{\alpha v} = 2CV-2\alpha V αvαf=2CV−2αV
我们令导数为0,即:
C V = α V CV = \alpha V CV=αV
对于 C V = α V CV = \alpha V CV=αV这个公式是不是很熟悉,没错就是特征值,特征向量的定义式,其中 α \alpha α即是特征值,V即是特征向量,这也就解释了文章开头提到的问题,为啥PCA是求特征值与特征向量即特征值分解。
最后我们把求出来的偏导带入到 f ( V , α ) f(V,\alpha) f(V,α)中,即:
f ( V , α ) = α f(V,\alpha) = \alpha f(V,α)=α
由公式可知散度的值只由 α \alpha α来决定, α \alpha α的值越大,散度越大,也就是说我们需要找到最大的特征值与对应的特征向量。
特征值、特征向量
通过上面的推导我们知道了为啥要求特征值与特征向量,那么特征向量和特征值到底有什么意义呢?
首先,我们要明确一个矩阵和一个向量相乘有什么意义?即等式左边 C V CV CV的意义。矩阵和向量相乘实际上是把向量投影到矩阵的列空间,更通俗的理解就是对该向量做个旋转或伸缩变换,我们来看个例子。
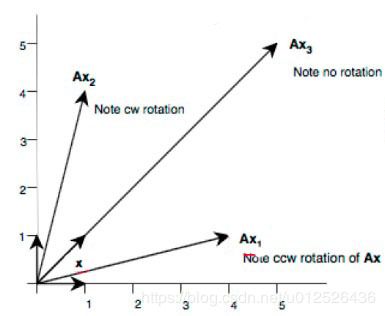
从图中我们可以发现( X 3 X_3 X3为特征向量, X 1 , X 2 X_1,X_2 X1,X2为非特征向量):
-
一个矩阵和该矩阵的非特征向量相乘是对该向量的旋转变换,如 A X 1 , A X 2 AX_1,AX_2 AX1,AX2。
-
一个矩阵和该矩阵的特征向量相乘是对该向量的伸缩变换,如 A X 3 AX_3 AX3。
再看下等式右边 α V \alpha V αV,一个标量和一个向量相乘,没错就是对一个向量的伸缩变换。
通过以上分析,我们发现, C V = α V CV = \alpha V CV=αV的意思就是:特征向量在矩阵的伸缩变换下,那到底伸缩了多少倍呢?伸缩了“特征值”倍。
降维
接下来就是我们的最后一步了,我们把所有的特征值按照降序排列,根据我们最终需要的维度 d d d来选取前 d d d大的特征向量,并组成一个矩阵 W ∗ = ( w 1 , w 2 , . . . , w d ) W^* = (w_1,w_2,...,w_d) W∗=(w1,w2,...,wd),把原始样本数据与投影矩阵做矩阵乘法,即可得到降维后的结果。对于超参数 d d d的选择,可采用交叉验证来选择。最后上一张PCA的流程图。
总结
对于特征较多的数据样本,计算协方差矩阵是很耗时的操作,因此,在实践中会对数据样本做奇异值分解来代替协方差矩阵的特征值分解,感兴趣的读者可参阅其他博文。
降维对于维度较高的数据集是很有必要的,虽然部分数据被舍弃了,但是舍弃这部分信息之后能使样本的采样密度增加,这正是降维的重要动机,另一方面,当数据受到噪声影响时,最小的特征值所对应的特征向量往往与噪声有关,将他们舍弃能在一定程度上起到去噪的效果。