数学建模——线性规划与整数规划

线性规划

线性规划问题是在一组线性约束条件的限制下，求一线性目标函数最大或最小的问题。
线性规划问题标准形式：
$$\begin{gathered} maxz=\sum _{j=1}^n{c}_j{x}_j, \\ \{\begin{array}{l}\sum _{j=1}^n{a}_{ij}{x}_j=b_i,i=1,2,...,m,\\ x_j⩾0,j=1,2,,...,n.\end{array} \end{gathered}$$
matlab中线性规划标准形式：
$$\begin{gathered} \underset{x}{\min }{\text{f}}^T\text{x}, \\ s.t.\{\begin{array}{l}\text{A}\cdot \text{x}⩽\text{b},\\ Aeq\cdot \text{x}=beq,\\ lb⩽\text{x}⩽ub.\end{array} \end{gathered}$$
在实际问题中常常将题目中的约束条件转化为矩阵或向量进行运算，上式中f，x，b，beq，lb，ub为列向量，其中f称为价值向量，b成为资源向量，A，Aeq为矩阵。

例：已知x，y满足以下约束条件$$\{\begin{array}{l}x-4y⩽-3\\ 3x+5y⩽25\\ x⩾1\end{array}$$
则z=2x+y的最小值是：

首先，将题中所给条件化为matlab标准型
$$\begin{gathered} \min \omega =2x+y, \\ s.t.\{\begin{array}{l}\left[\begin{array}{cc}1& -4\\ 3& 5\\ -1& 0\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]⩽\left[\begin{array}{c}-3\\ 25\\ -1\end{array}\right]\end{array} \end{gathered}$$
matlab求解线性规划问题的函数为linprog函数，
函数命令为[x, fval]=lingprog(f, A, b, Aeq, Beq, lb, ub)；
其中x为决策变量矩阵，fval为最优解，Aeq，beq，lb，ub可缺省。

所以上题matlab代码为：

f=[2;1];
a=[1,-4;3,5;-1,0];
b=[-3;25;-1];
[x,y]=linprog(f,a,b,[],[],zeros(2,1));%没有等式约束
x,y

输出结果为：

>> Untitled

Optimal solution found.


x =

    1.0000
    1.0000


y =

    3.0000

整数规划

当数学规划的变量都限制为整数时，便称为整数规划。
当线性规划的变量都限制为整数时，便称为整数线性规划。
常用求解方法：
（1）分支定界法——可求纯或混合整数线性规划。
（2）割平面法——可求纯或混合整数线性规划。
（3）隐枚举法——求解“0-1”整数规划。
过滤隐枚举法
分支隐枚举法
（4）匈牙利法——解决指派问题（“0-1”规划特殊情形）。
（5）蒙特卡洛法——求解各种类型规划。

分支定界法

分支定界法多借用二叉树结构进行求解，整数规划对应的线性规划可称为其对应的松弛问题（LP）。

分枝定界法的一般步骤：
设整数规划对应的线性规划为松弛问（B）
（1）若整数规划对应的线性规划没有可行解，则整数规划也没有可行解，停止计算。
（2）若线性规划有最优解，并符合整数规划条件，则线性规划的最优解即为整数规划的最优解，停止计算。
（3）若线性规划有最优解，但不符合整数规划的整数条件，转入以下步骤。
（4）设问题B的最优解X*不符合整数要求，则选择一个分量分支，
$$(C)\{\begin{array}{l}(B)\\ X_j⩾[x_j^{\ast }]+1\end{array}(D)\{\begin{array}{l}(B)\\ X_j⩽[x_j^{\ast }]\end{array}$$
分支（C）（D）称为后继问题，这两个子问题的最优解的目标函数值都不会比原线性规划问题的最优解的目标函数值更大。如果这两个问题的最优解仍不是整数解，则继续选择一个非整数的变量，继续将这个子问题分解为两个更下一级的子问题。这个过程称为“分支(Branch)
每一次分支得到的子问题最优解的目标函数值，都小于或等于分支前问题的最优解的目标函数值。非整数解的最大值作为新的上界。如果某一个子问题的最优解是整数解，就作为整数规划最优目标函数值的下界。多个时取最大值。最后的下界为整数规划的最优解。如果某一个子问题的解还不是整数解，但这个非整数解的目标函数值已经小于这个下界，那么这个子问题就不必再进行分支。不然需重复进行分支。确定整数解目标函数值上下界并不断更新，“剪除” 目标函数值小于下界的分支的过程，称为定界(Bound) 。

割平面法

一般步骤：

（1）若整数规划对应的线性规划没有可行解，则整数规划也没有可行解，停止计算。
（2）若线性规划有最优解，并符合整数规划条件，则线性规划的最优解即为整数规划的最优解，停止计算。
（3）若线性规划有最优解，但不符合整数规划的整数条件，转入以下步骤。
（4）从线性规划的最优解中任选一个不为整数的分量x_r，将最优单纯形表中该行的系数a_rj’和b_r’分量分解为整数部分和小数部分的和，并以该行为源行，按下式做割平面方程
$$\sum _{j=m+1}^n(-f_{rj})x_j⩽-f_r$$
-f_rj为a_rj’的小数部分，f_r为b_r’的小数部分。
（5）将所得的割平面方程作为一个新的约束条件置于最优单纯形表中（同时增加一个单位列向量）。用对偶单纯形表法求出新的最优解，返回第一步。

隐枚举法

隐枚举法适用于整数规划中的“0-1”规划。
一般步骤：

决策变量为x_i( i=1, 2, 3, …)
（1）将目标函数统一为求最小值，将约束条件转化为A x ≥ b形式，将目标函数中系数为负的变量x_i转化为系数为正的变量x_i’，其中x_i’=1-x_i，使目标函数和约束条件中的各项系数递增。
（2）从x_i=0项（即x₁=x₂=x₃=…=0）开始枚举。
（3）计算出该次枚举对应的目标函数值，若大于已有可行解的函数值，剪枝，继续枚举；若小于已有可行解的函数值，或还无可行解，执行下一步。
（4）检查解是否满足约束条件（检察出一个不满足便不需继续检查）
若不满足，则此时的枚举值不是可行解，继续枚举;
若满足，则更新可行解和目标函数值z₀。可行解0…0x_j…x₁（前面’0’的个数可能为0），那么只要是以x_j…x₁结尾和只将x_j…x₁中某些位由0变为1的解的目标函数取值一定大于z₀，剪枝，再进行枚举。
最终剩下的便是最优解。

匈牙利法

匈牙利法常用来解决指派问题。
指派问题：
例：
拟分配n人去做n项工作，每人做且仅做一项工作，若分配第i人去做第j项工作，需花费c_ij单位时间，问应如何分配工作才能使工人花费的总时间最少。

引入0-1变量
$$x_{ij}=\{\begin{array}{l}1，第i人做第j项工作\\ 0，第i人不做第j项工作\end{array}，i，j=1,2,\dots n.$$
上述指派问题的数学模型为
$$\begin{gathered} \min \sum _{i=1}^n\sum _{j=1}^n{c}_{ij}{x}_{ij}, \\ s.t.\{\begin{array}{l}\sum _{j=1}^n{x}_{ij}=1,i=1,2,3...n,\\ \sum _{i=1}^n{x}_{ij}=1,j=1,2,3...n,\\ x_{ij}=0或1,i,j=1,...n.\end{array} \end{gathered}$$
上述指派问题的可行解可以用一个矩阵表示，其每行每列有且仅有一个元素为1，其余元素均为0；还可以用1，2，3，…，n中的一个置换表示。

该问题的效率矩阵可表示为：
$$\left[\begin{array}{cccc}{c}_{11}& c_{12}& ...& c_{1n}\\ c_{21}& c_{22}& ...& c_{2n}\\ ⋮& ⋮& & ⋮\\ c_{n1}& c_{n2}& ...& c_{nn}\end{array}\right]$$
用匈牙利法求解指派问题具体过程可参照以下，这里不过多赘述。

https://blog.csdn.net/z464387937/article/details/51227347

蒙特卡洛法

蒙特卡洛法是通过计算机模拟产生大量随机数进行模拟的方法。
例：
非线性整数规划为：
$$\begin{gathered} \max z=x_1^2+z_2^2+3x_3^2+4x_4^2+2x_5^2-8x_1-2x_2-3x_3-x_4-2x_5, \\ s.t.\{\begin{array}{l}0⩽x_i⩽99,i=1,2,...,5\\ x_1+x_2+x_3+x_4+x_5⩽400\\ x_1+2x_2+2x_3+x_4+6x_5⩽800\\ 2x_1+x_2+6x_3⩽200\\ x_3+x_4+5x_5⩽200.\end{array} \end{gathered}$$
本题使用随机数在可行域内产生10⁶个点，其中至少有一点落在高值区域的概率极高。

matlab实现：

function mente
rand('state',sum(clock));
p0=0;
tic
for i=1:10^6
    x=randi([0,99],1,5);
    [f,g]=mengte(x);
    if all(g<=0)
        if p0<f
            x0=x;p0=f;
        end
    end
end
x0,p0
toc

function[f,g]=mengte(x)

f=x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)^2-8*x(1)-2*x(2)-3*x(3)-x(4)-2*x(5);
g=[sum(x)-400
    x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800
    2*x(1)+x(2)+6*x(3)-200
    x(3)+x(4)+5*x(5)-200];

结果：

>> mente

x0 =

    41    98     2    99    10


p0 =

       50052

历时 0.903785 秒。
>> 

因为是随机产生的数字，所以每次运行结果不同。

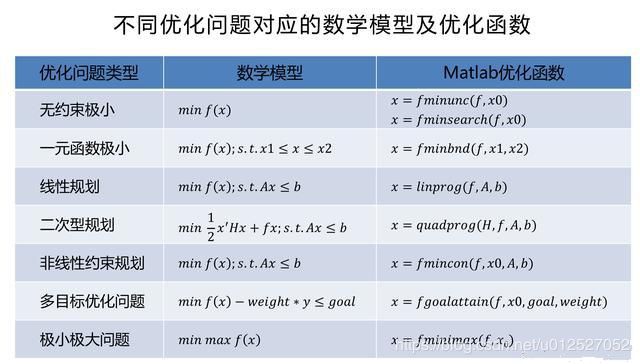
matlab解决优化问题

matlab内置有优化工具箱，可以解决绝大多数优化问题

Optimization Toolbox™ 提供了寻找最小化或最大化目标并同时满足约束条件的函数。工具箱中包括了线性规划 (LP)、混合整数线性规划 (MILP)、二次规划 (QP)、非线性规划 (NLP)、约束线性最小二乘法、非线性最小二乘和非线性方程的求解器。
详见Optimization Toolbox官方网站
或https://blog.csdn.net/cclethe/article/details/77200997

matlab常用解决优化问题的函数有：

转自头条号/算法集市

对于整数规划问题，matlab内置了intlinprog函数

函数命令为：
[x, fval]=intlinprog(f, intcon, A, b, Aeq, beq, lb, ub)
其中变量intcon是有整数要求的决策变量的下标组成的列向量，其余变量与线性规划相同。

数学模型为：
$$\begin{gathered} \underset{x}{\min }{\text{f}}^T\text{x}, \\ s.t.\{\begin{array}{l}\text{x}(intcon)为整数\\ \text{A}\cdot \text{x}⩽\text{b}\\ Aeq\cdot \text{x}=beq\\ lb⩽\text{x}⩽ub\end{array} \end{gathered}$$
intlinprog函数中的决策变量只能是一维，因此只有将二维决策变量转化为一维才能继续使用该函数
例：
以下指派问题中指派矩阵为：
$$\left[\begin{array}{ccccc}3& 8& 2& 10& 3\\ 8& 7& 2& 9& 7\\ 6& 4& 2& 7& 5\\ 8& 4& 2& 3& 5\\ 9& 10& 6& 9& 10\end{array}\right]$$
将二维决策变量x_ij（i，j=1，2，3，4，5）变为一维决策变量y_k（k=1，2，3，…，25）

matlab代码：

c=[3,8,2,10,3;8,7,2,9,7;6,4,2,7,5;8,4,2,3,5;9,10,6,9,10];
c=c(:); a=zeros(10,25); intcon =1:25;
for i=1:5
    a(i,(i-1)*5+1:5*i)=1;
    a(5+i,i:5:25)=1;
end
b = ones(10,1);
lb = zeros(25,1);
ub = ones(25,1);
x = intlinprog(c,intcon,[],[],a,b,lb,ub);
x = reshape(x,[5,5])

输出：

>> 
LP:                Optimal objective value is 21.000000.                                            


Optimal solution found.

Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value,
options.AbsoluteGapTolerance = 0 (the default value). The intcon variables are integer within tolerance,
options.IntegerTolerance = 1e-05 (the default value).


x =

     0     0     0     0     1
     0     0     1     0     0
     0     1     0     0     0
     0     0     0     1     0
     1     0     0     0     0

>> 

若问题中决策变量为一维，则与线性规划无太大差别。

参考文献：
[1]司守奎，孙兆亮．数学建模算法与应用[M]．第二版．北京：国防工业出版社，2018.
[2]部分资料来源于互联网