haar特征简单分析
内容来自网上博客(地址:http://lib.csdn.net/article/opencv/29324),我认为讲解的比较好。简单描述一下haar特征
haar特征生成
当然网上还可以看到haar的其它一些扩展特征类型,这些扩展类型原理和基本类型一样,只是角度或者形状不同,且实际效果并不是特别好,所以这里就不介绍了
在实际中,Haar特征可以在检测窗口中由放大+平移产生一系列子特征,但是白:黑区域面积比始终保持不变。
对于 m×m 子窗口,我们只需要确定了矩形左上顶点A(x1,y1)和右下顶点B(x2,y2) ,即可以确定一个矩形;如果这个矩形还必须满足下面两个条件(称为(s, t)条件,满足(s, t)条件的矩形称为条件矩形):
1) x 方向边长必须能被自然数s 整除(能均等分成s 段);
2) y 方向边长必须能被自然数t 整除(能均等分成t 段);
则 , 这个矩形的最小尺寸为s×t 或t×s, 最大尺寸为[m/s]·s×[m/t]·t 或[m/t]·t×[m/s]·s;其中[ ]为取整运算符。
下面列出了,在不同子窗口大小内,特征的总数量
| 窗口大小 | 36x36 | 30x30 | 24x24 | 20x20 | 16x16 |
|---|---|---|---|---|---|
| 特征数量 | 816264 | 394725 | 162366 | 78460 | 32384 |
计算方法
haar特征就是一些矩形区域,同一个类型的矩形区域不管放大多少,黑白面积比都不变。用一个类型的haar放大N倍,盖住原图像中的目标区域,把haar特征白色区域盖住的像素点的值的和 减去 该haar特征黑色区域的像素点的值的和得到的结果作为haar特征值
在opencv代码中,是这样计算haar特征值的:
Haar特征值 = 整个Haar区域内像素和×权重 + 黑色区域内像素和×权重
公式表示就是
上图中权重分布:
特征 x2 y2 x2_y2 类型权重: W(all) = 1 , W(black) = -2
特征 x3 y3 类型权重: W(all) = 1 , W(black) = -3
为什么要设置权重? 设置权值就是为了抵消面积不等带来的影响,保证所有Haar特征的特征值在灰度分布绝对均匀的图中为
以x3特征为例,在放大+平移过程中白:黑:白面积比始终是1:1:1。首先在红框所示的检测窗口中生成大小为3个像素的最小x3特征;之后分别沿着x和y平移产生了在检测窗口中不同位置的大量最小3像素x3特征;然后把最小x3特征分别沿着x和y放大,再平移,又产生了一系列大一点x3特征;然后继续放大+平移,重复此过程,直到放大后的x3和检测窗口一样大。这样x3就产生了完整的x3系列特征
特征值含义
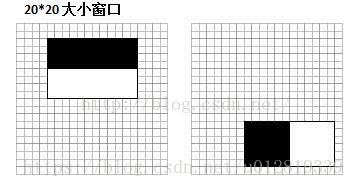
选取了MIT人脸库中2706个大小为20*20的人脸正样本图像,计算下图中的两类不同的Haar特征值
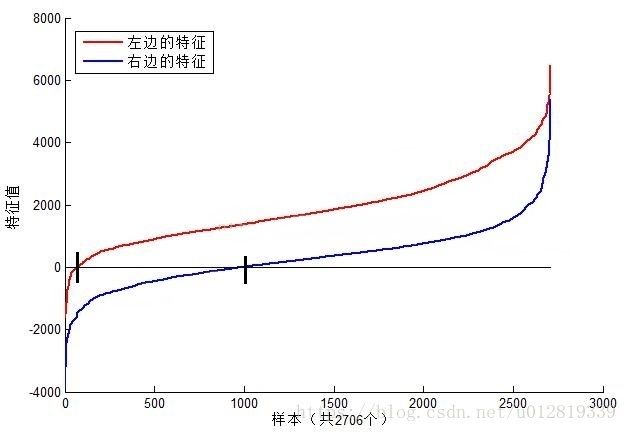
可以看到,图1中2个不同Haar特征在同一组样本中具有不同的特征值分布,左边特征计算出的特征值基本都大于0,而右边特征的特征值基本均匀分布于0两侧(分布越均匀对样本的区分度越小)。所以,正是由于样本中Haar特征值分布不同,导致了不同Haar特征分类效果不同。显而易见,对样本区分度越大的特征分类效果越好,即红色曲线对应图1中的的左边Haar特征分类效果好于右边Haar特征。那么看到这里,应该理解了下面2个问题:
在检测窗口通过平移+放大可以产生一系列Haar特征,这些特征由于位置和大小不同,分类效果也各异;
通过计算Haar特征的特征值,可以有将图像矩阵映射为1维特征值,有效实现了降维
在检测窗口通过平移+放大可以产生一系列Haar特征,这些特征由于位置和大小不同,分类效果也各异;通过计算Haar特征的特征值,可以有将图像矩阵映射为1维特征值,有效实现了降维
特征值标准化
从上图中发现,仅仅一个12*18大小的Haar特征计算出的特征值变化范围从-2000~+6000,跨度非常大。这种跨度大的特性不利于量化评定特征值,所以需要进行“标准化”,压缩特征值范围。假设当前检测窗口中的图像为i(x,y),当前检测窗口为w*h大小(例如图6中为20*20大小),OpenCV采用如下方式“标准化”:
计算检测窗口中间部分 (w−2)∗(h−2) ( w − 2 ) ∗ ( h − 2 ) 的图像的灰度值和灰度值平方和:
sum=∑i(x,y) s u m = ∑ i ( x , y )
sqsum=∑i2(x,y) s q s u m = ∑ i 2 ( x , y )计算平均值:
mean=sumw∗h m e a n = s u m w ∗ h
sqmean=sqsumw∗h s q m e a n = s q s u m w ∗ h计算标准化因子:
varNormFactor=sqmean−mean2−−−−−−−−−−−−−−√ v a r N o r m F a c t o r = s q m e a n − m e a n 2标准化特征值:
normValue=featureValuevarNormFactor n o r m V a l u e = f e a t u r e V a l u e v a r N o r m F a c t o r
之后按照上述公式求出varNormFactor后,使用标准化后的特征值normValue与阈值对比