数据分析——“玻璃的类型”数据集
文章目录
- 0.数据集介绍
- 1.玻璃数据集读取与分析
- 2.变量关系可视化(平行坐标图)
- 3.属性对相关性可视化
0.数据集介绍
多类别分类问题与二元分类问题类似,不同之处在于它有多个离散的输出,而不是只有两个。回顾探测未爆炸的水雷的问题,它的输出只有两种可能性:声纳探测的物体是岩石或者水雷。而红酒口感评分问题根据其化学成分会产生几个可能的输出(其口感评分值是从 3 分到 8 分)。但是对于红酒口感评分问题,口感评分值存在有序的关系。打 5 分的红酒要好于打 3 分的,但是要劣于打 8 分的。对于多类别分类问题,输出结果是不存在这种有序关系的。该节所用数据集根据玻璃的化学成分来判断玻璃的类型,目标是确定玻璃的用途。玻璃的用途包括建筑房间用玻璃、车辆上的玻璃、玻璃容器等。确定玻璃的用途类型是为了鉴证。例如在一个车祸或犯罪现场,会有玻璃的碎片,确定这些玻璃碎片的用途、来源,有助于确定谁是过错方或者谁是罪犯。
1.玻璃数据集读取与分析
import pandas as pd
from pandas import DataFrame
from pylab import *
import matplotlib.pyplot as plot
target_url = ("https://archive.ics.uci.edu/ml/machine-learning-databases/glass/glass.data")
## 读取数据集
glass = pd.read_csv(target_url,header=None,prefix="V")
glass.columns = ['Id', 'RI', 'Na', 'Mg', 'Al', 'Si', 'K', 'Ca', 'Ba', 'Fe', 'Type']
print(glass.head())
## 数据集统计
summary = glass.describe()
print(summary)
ncol1 = len(glass.columns)
## 去掉Id列
glassNormalized = glass.iloc[:, 1:ncol1]
ncol2 = len(glassNormalized.columns)
summary2 = glassNormalized.describe()
print(summary2)
## 归一化
for i in range(ncol2):
mean = summary2.iloc[1, i]
sd = summary2.iloc[2, i]
glassNormalized.iloc[:,i:(i + 1)] = (glassNormalized.iloc[:,i:(i + 1)] - mean) / sd
## 绘制箱线图
array = glassNormalized.values
boxplot(array)
plot.xlabel("Attribute Index")
plot.ylabel(("Quartile Ranges - Normalized "))
show()
Id RI Na Mg Al Si K Ca Ba Fe Type
0 1 1.52101 13.64 4.49 1.10 71.78 0.06 8.75 0.0 0.0 1
1 2 1.51761 13.89 3.60 1.36 72.73 0.48 7.83 0.0 0.0 1
2 3 1.51618 13.53 3.55 1.54 72.99 0.39 7.78 0.0 0.0 1
3 4 1.51766 13.21 3.69 1.29 72.61 0.57 8.22 0.0 0.0 1
4 5 1.51742 13.27 3.62 1.24 73.08 0.55 8.07 0.0 0.0 1
Id RI Na Mg Al Si \
count 214.000000 214.000000 214.000000 214.000000 214.000000 214.000000
mean 107.500000 1.518365 13.407850 2.684533 1.444907 72.650935
std 61.920648 0.003037 0.816604 1.442408 0.499270 0.774546
min 1.000000 1.511150 10.730000 0.000000 0.290000 69.810000
25% 54.250000 1.516523 12.907500 2.115000 1.190000 72.280000
50% 107.500000 1.517680 13.300000 3.480000 1.360000 72.790000
75% 160.750000 1.519157 13.825000 3.600000 1.630000 73.087500
max 214.000000 1.533930 17.380000 4.490000 3.500000 75.410000
K Ca Ba Fe Type
count 214.000000 214.000000 214.000000 214.000000 214.000000
mean 0.497056 8.956963 0.175047 0.057009 2.780374
std 0.652192 1.423153 0.497219 0.097439 2.103739
min 0.000000 5.430000 0.000000 0.000000 1.000000
25% 0.122500 8.240000 0.000000 0.000000 1.000000
50% 0.555000 8.600000 0.000000 0.000000 2.000000
75% 0.610000 9.172500 0.000000 0.100000 3.000000
max 6.210000 16.190000 3.150000 0.510000 7.000000
RI Na Mg Al Si K \
count 214.000000 214.000000 214.000000 214.000000 214.000000 214.000000
mean 1.518365 13.407850 2.684533 1.444907 72.650935 0.497056
std 0.003037 0.816604 1.442408 0.499270 0.774546 0.652192
min 1.511150 10.730000 0.000000 0.290000 69.810000 0.000000
25% 1.516523 12.907500 2.115000 1.190000 72.280000 0.122500
50% 1.517680 13.300000 3.480000 1.360000 72.790000 0.555000
75% 1.519157 13.825000 3.600000 1.630000 73.087500 0.610000
max 1.533930 17.380000 4.490000 3.500000 75.410000 6.210000
Ca Ba Fe Type
count 214.000000 214.000000 214.000000 214.000000
mean 8.956963 0.175047 0.057009 2.780374
std 1.423153 0.497219 0.097439 2.103739
min 5.430000 0.000000 0.000000 1.000000
25% 8.240000 0.000000 0.000000 1.000000
50% 8.600000 0.000000 0.000000 2.000000
75% 9.172500 0.000000 0.100000 3.000000
max 16.190000 3.150000 0.510000 7.000000
玻璃数据的箱线图显示有相当数量的异常点,至少与前面的例子相比,异常点数量上是比较多的。玻璃数据集有几个因素可能会导致出现异常点。首先这是一个分类问题,在属性值和类别之间不需要存在任何连续性,也就是说不应期望在各种类别之间,属性值是相互接近的、近似的。另外一个玻璃数据比较独特的地方是它的数据是非平衡的。成员最多的类有76个样本,而成员最小的类只有9个样本。统计时,平均值可能是由成员最多的那个类的属性值决定,因此不能期望其他的类别也有相似的属性值。采取激进的方法来区分类别可能会达到较好的结果,但这也意味着预测模型需要跟踪不同类别之间复杂的边界。
2.变量关系可视化(平行坐标图)
import pandas as pd
from pandas import DataFrame
from pylab import *
import matplotlib.pyplot as plot
target_url = ("https://archive.ics.uci.edu/ml/machine-learning-databases/glass/glass.data")
## 读取数据集
glass = pd.read_csv(target_url,header=None,prefix="V")
glass.columns = ['Id', 'RI', 'Na', 'Mg', 'Al', 'Si', 'K', 'Ca', 'Ba', 'Fe', 'Type']
glassNormalized = glass
ncols = len(glassNormalized.columns)
nrows = len(glassNormalized.index)
summary = glassNormalized.describe()
nDataCol = ncols - 1
## 归一化
for i in range(ncols - 1):
mean = summary.iloc[1, i]
sd = summary.iloc[2, i]
glassNormalized.iloc[:,i:(i + 1)] = (glassNormalized.iloc[:,i:(i + 1)] - mean) / sd
for i in range(nrows):
#plot rows of data as if they were series data
dataRow = glassNormalized.iloc[i,1:nDataCol]
labelColor = glassNormalized.iloc[i,nDataCol]/7.0
dataRow.plot(color=plot.cm.RdYlBu(labelColor), alpha=0.5)
plot.xlabel("Attribute Index")
plot.ylabel(("Attribute Values"))
plot.show()
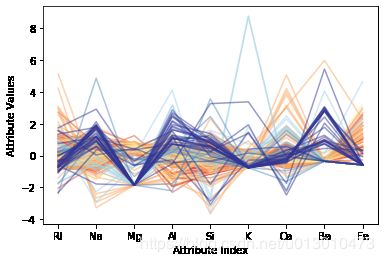
平行坐标图可能对此数据集揭示的信息更多。上图为其平行坐标图,数据根据输出类别用不同的颜色标记(每种颜色代表一种类别,共有6种类别,6 种颜色),有些类别区分度很好。例如,深蓝色的线聚集度很好,在某些属性上与其他类别的区分度也很好。深蓝的线在某些属性上经常处于数据的边缘,也就是说,是这些属性上的异常点。浅蓝的线在某些属性上也与深蓝的线一样,处于边缘地带,但是数量上要比深蓝的少,而且两者都在边缘地带时的所属的属性也不尽相同。棕色的线聚集性也很好,但其取值基本上在中心附近。在多类别分类问题中,平行坐标图颜色的选择与回归问题中的方式类似,将目标类别(标签)除以其最大值,然后再基于此数值选择颜色。
3.属性对相关性可视化
import pandas as pd
from pandas import DataFrame
from pylab import *
import matplotlib.pyplot as plot
target_url = ("https://archive.ics.uci.edu/ml/machine-learning-databases/glass/glass.data")
## 读取数据集
glass = pd.read_csv(target_url,header=None,prefix="V")
glass.columns = ['Id', 'RI', 'Na', 'Mg', 'Al', 'Si', 'K', 'Ca', 'Ba', 'Fe', 'Type']
## 计算所有实值列(包括目标)的相关矩阵
corMat = DataFrame(glass.iloc[:,1:-1].corr())
print(corMat)
## 使用热图可视化相关矩阵
plot.pcolor(corMat)
plot.show()
RI Na Mg Al Si K Ca \
RI 1.000000 -0.191885 -0.122274 -0.407326 -0.542052 -0.289833 0.810403
Na -0.191885 1.000000 -0.273732 0.156794 -0.069809 -0.266087 -0.275442
Mg -0.122274 -0.273732 1.000000 -0.481799 -0.165927 0.005396 -0.443750
Al -0.407326 0.156794 -0.481799 1.000000 -0.005524 0.325958 -0.259592
Si -0.542052 -0.069809 -0.165927 -0.005524 1.000000 -0.193331 -0.208732
K -0.289833 -0.266087 0.005396 0.325958 -0.193331 1.000000 -0.317836
Ca 0.810403 -0.275442 -0.443750 -0.259592 -0.208732 -0.317836 1.000000
Ba -0.000386 0.326603 -0.492262 0.479404 -0.102151 -0.042618 -0.112841
Fe 0.143010 -0.241346 0.083060 -0.074402 -0.094201 -0.007719 0.124968
Ba Fe
RI -0.000386 0.143010
Na 0.326603 -0.241346
Mg -0.492262 0.083060
Al 0.479404 -0.074402
Si -0.102151 -0.094201
K -0.042618 -0.007719
Ca -0.112841 0.124968
Ba 1.000000 -0.058692
Fe -0.058692 1.000000
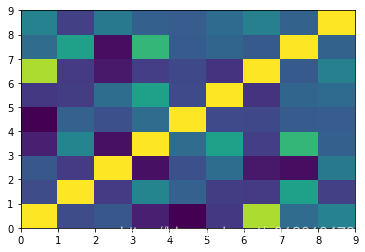
关联热图显示了属性之间绝大多数是弱相关的,说明属性之间绝大多数是相互独立的,这是件好事情。标签(目标类别)没有出现在热图中,因为目标(类别)只取几个离散值中的一个。不包括目标类别无疑减少了关联热图所能揭示的信息。