推荐-基于bandit的主题冷启动在线学习策略
推荐-基于bandit的主题冷启动在线学习策略
推荐系统里面有两个经典问题:EE问题和冷启动问题。
什么是EE问题?又叫exploit-explore问题。exploit就是:对用户比较确定的兴趣,当然要利用开采迎合,好比说已经挣到的钱,当然要花;explore就是:光对着用户已知的兴趣使用,用户很快会腻,所以要不断探索用户新的兴趣才行,这就好比虽然有一点钱可以花了,但是还得继续搬砖挣钱,不然花完了就得喝西北风。
除了bandit算法之外,还有一些其他的explore的办法,比如:在推荐时,随机地去掉一些用户历史行为(特征)。
0 Beta分布
但是我发现Beta分布就很少会用这样可以凭直觉感知的方法来解释它的用处在哪里,而且Beta分布经常会和一些复杂的概念一起出现,比如“共轭先验”和“顺序统计量”。
我们预期这个运动员一个赛季的击球率大约是0.27,但在0.21到0.35之间都是合理的。这种情况可以用一个参数α=81和 β=219的Beta分布来表示:![]()
x轴代表的是他的击球率。因此请注意在这个实例当中,不仅y轴是概率(或者更准确地说是概率密度),x轴也是(击球率就是一次击球击中的概率)。这个Beta分布表示了一个概率的概率分布。
- 平均数(期望)是α/(α+β)=81/(81+219)=0.270
- 这个分布几乎全部分布在(0.2,0.35)这个范围之间,也就是击球率的合理范围。
β分布的形状取决于α和β的值。贝叶斯分析中大量使用了β分布。
当你将参数α和β都设置为1时,该分布又被称为均匀分布(uniform distribution)。尝试不同的α和β取值,看看分布的形状是如何变化的。
当然,从该分布来看,beta.pdf(x,a,b)中除了a,b两个数字参数之外,还有x表征的概率因素在其中。这里x,相当于模拟了不同概率条件下,概率密度的走势,所以横轴是可以代表概率值,概率函数最大值(y的最大值)也代表概率最大值(x最大值)。
参考:
直观理解Beta分布
如何在Python中实现这五类强大的概率分布
1 bandit介绍
主要来源:《Bandit算法与推荐系统》,首发于《程序员》杂志
1.1 bandit简介
bandit算法是一种简单的在线学习算法,常常用于尝试解决这两个问题。
bandit算法来源于历史悠久的赌博学,它要解决的问题是这样的:
一个赌徒,要去摇老虎机,走进赌场一看,一排老虎机,外表一模一样,但是每个老虎机吐钱的概率可不一样,他不知道每个老虎机吐钱的概率分布是什么,那么每次该选择哪个老虎机可以做到最大化收益呢?这就是多臂赌博机问题(Multi-armed bandit problem, K-armed bandit problem, MAB)。
衡量不同bandit算法在解决多臂问题上的效果?首先介绍一个概念,叫做累积遗憾(regret):这里我们讨论的每个臂的收益非0即1,也就是伯努利收益。定义累积遗憾(regret) :
然后,每次选择后,计算和最佳的选择差了多少,然后把差距累加起来就是总的遗憾。
1.2 常用的bandit算法——Thompson sampling算法
Thompson sampling算法:假设每个臂是否产生收益,其背后有一个概率分布,产生收益的概率为p。每次选择臂的方式是:用每个臂现有的beta分布产生一个随机数b,选择所有臂产生的随机数中最大的那个臂去摇。
1.3 常用的bandit算法——UCB算法
这个公式反映一个特点:均值越大,标准差越小,被选中的概率会越来越大,同时哪些被选次数较少的臂也会得到试验机会。
1.4 常用的bandit算法——Epsilon-Greedy算法
有点类似模拟退火的思想:
选一个(0,1)之间较小的数作为epsilon
每次以概率epsilon做一件事:所有臂中随机选一个
每次以概率1-epsilon 选择截止到当前,平均收益最大的那个臂。
是不是简单粗暴?epsilon的值可以控制对Exploit和Explore的偏好程度。越接近0,越保守,只想花钱不想挣钱。
1.5 常用的bandit算法——朴素bandit算法
最朴素的bandit算法就是:先随机试若干次,计算每个臂的平均收益,一直选均值最大那个臂。这个算法是人类在实际中最常采用的,不可否认,它还是比随机乱猜要好。
把几个模型的结果,进行10000次模型。可得以下的图:
2 bandit的延伸应用与模型
2.1 bandit算法与线性回归
**UCB解决Multi-armed bandit问题的思路是:用置信区间。**置信区间可以简单地理解为不确定性的程度,区间越宽,越不确定,反之亦反之。UCB算法加入特征信息,单纯的老虎机回报情况就是老虎机自己内部决定的,而在广告推荐领域,一个选择的回报,是由User和Item一起决定的,如果我们能用feature来刻画User和Item这一对CP,在每次选择item之前,通过feature预估每一个arm(item)的期望回报及置信区间,选择的收益就可以通过feature泛化到不同的item上。
LinUCB算法有一个很重要的步骤,就是给User和Item构建特征:
原始用户特征
- 人口统计学:性别特征(2类),年龄特征(离散成10个区间)
- 地域信息:遍布全球的大都市,美国各个州
- 行为类别:代表用户历史行为的1000个类别取值
原始文章特征
- URL类别:根据文章来源分成了几十个类别
- 编辑打标签:编辑人工给内容从几十个话题标签中挑选出来的
2.2 bandit算法与协同过滤
每一个推荐候选item,都可以根据用户对其偏好不同(payoff不同)将用户聚类成不同的群体,一个群体来集体预测这个item的可能的收益,这就有了协同的效果,然后再实时观察真实反馈回来更新用户的个人参数,这就有了bandit的思想在里面。
另外,如果要推荐的候选item较多,还需要对item进行聚类,这样就不用按照每一个item对user聚类,而是按照每一个item的类簇对user聚类,如此以来,item的类簇数相对于item数要大大减少。
COFIBA算法
基于这些思想,有人提出了算法COFIBA(读作coffee bar)13,简要描述如下:
在时刻t,用户来访问推荐系统,推荐系统需要从已有的候选池子中挑一个最佳的物品推荐给他,然后观察他的反馈,用观察到的反馈来更新挑选策略。 这里的每个物品都有一个特征向量,所以这里的bandit算法是context相关的。 这里依然是用岭回归去拟合用户的权重向量,用于预测用户对每个物品的可能反馈(payoff),这一点和linUCB算法是一样的。
对比LinUCB算法,COFIBA算法的不同有两个:
- 基于用户聚类挑选最佳的item(相似用户集体决策的bandit)
- 基于用户的反馈情况调整user和item的聚类(协同过滤部分)
也就是user(人群聚类)、item(主题聚类)双料聚类。
3 python实现bandit在线学习策略
之前提到的几个code可在github之中看到:
- COFIBA算法:https://github.com/qw2ky/CoLinUCB_Revised/blob/master/COFIBA.py
- 常规bandit算法:https://gist.github.com/anonymous/211b599b7bef958e50af#file-bandit_simulations-py-L95
- Hybrid LinUCB:https://github.com/Fengrui/HybridLinUCB-python
笔者简单的基于常规bandit算法进行了一些尝试。
3.1 几款bandit常规模型的评估
code可见:anonymous/bandit_simulations.py
之前code主要是,输入了5个主题(K)下的10000个样本(num_samples ),迭代了100次(number_experiments )。
true_rewards抽取了单个样本来看,就是五个主题里面,第1,4个被提及了,其余的没有被提及。
array([[ True, False, False, True, False]])
CTRs_that_generated_data 点击可能性是用来评估regret。run_bandit_dynamic_alg函数输出的是,该模型下,该次迭代的regret值。
'''
main code
'''
# define number of samples and number of choices
num_samples = 10000
K = 5 # number of arms
number_experiments = 100
regret_accumulator = np.zeros((num_samples,5))
for i in range(number_experiments):
# 五套算法各自迭代100次的累加regret
print ("Running experiment:", i+1)
true_rewards,CTRs_that_generated_data = generate_bernoulli_bandit_data(num_samples,K)
regret_accumulator[:,0] += run_bandit_dynamic_alg(true_rewards,CTRs_that_generated_data,random)# (10000,)
regret_accumulator[:,1] += run_bandit_dynamic_alg(true_rewards,CTRs_that_generated_data,naive)
regret_accumulator[:,2] += run_bandit_dynamic_alg(true_rewards,CTRs_that_generated_data,epsilon_greedy)
regret_accumulator[:,3] += run_bandit_dynamic_alg(true_rewards,CTRs_that_generated_data,UCB)
regret_accumulator[:,4] += run_bandit_dynamic_alg(true_rewards,CTRs_that_generated_data,UCB_bernoulli)
plt.semilogy(regret_accumulator/number_experiments) # (10000, 5) / 100
plt.title('Simulated Bandit Performance for K = 5')
plt.ylabel('Cumulative Expected Regret')
plt.xlabel('Round Index')
plt.legend(('Random','Naive','Epsilon-Greedy','(1 - 1/t) UCB','95% UCB'),loc='lower right')
plt.show()
输出的结果即为:
regret最大代表误差越大,这边笔者的实验室UCB优先级高一些。
3.2 基于bandit的主题冷启动强化策略
首轮纯冷启动,会主动推给用户随机的10个主题样例,获得前期样本; 后进行迭代操作。
这边笔者在模拟实际情况,譬如在做一个新闻推荐的内容,需要冷启动。
假设该新闻平台主要有五个主题['news','sports','entertainment','edu','tech'],需要以主题推送给不同的用户。
3.2.1 第一轮冷启动
那么,假设笔者自己去看,一开始系统先随机推送10次内容于首页,看这些文章内容哪些被点击了,然后整理成变量top10 。那么,这里的意思就是,笔者打开APP的头10次,都是随机推送了,然后第一次,我点击了‘sports’,'edu'两个主题的内容,即被记录下来,这么模拟操作了10次。
topics = ['news','sports','entertainment','edu','tech']
top10 = [['sports','edu'],['tech','sports'],['tech','entertainment','edu'],['entertainment'],['sports','tech','sports']
,['edu'],['tech','news'],['tech','entertainment'],['tech'],['tech','edu']]
以上的内容进入bandit进行策略优化:
# generator data
true_rewards = generate_bandit_data(top10,topics)
# bandit model
estimated_beta_params = mBandit(true_rewards,UCB)
print('Cold boot ...')
prob1 = BanditProbs(estimated_beta_params,topics,printf = True,plotf = True)
其中的主题概率得分为:
【news】 topic prob is : 0.01
【sports】 topic prob is : 0.5
【entertainment】 topic prob is : 0.5
【edu】 topic prob is : 0.5
【tech】 topic prob is : 0.99
结果显示,进行了10次初始尝试,笔者对tech科技主题的偏好非常高,远远高于其他主题。
3.2.2 第二轮迭代
那么有了第一轮10次的基本经验,在这上面继续迭代。迭代的逻辑是:笔者接下来看一条,就会记录一条,导入模型进行迭代计算。
topic_POI = [['edu','news']]
true_rewards = generate_bandit_data(topic_POI,topics)
estimated_beta_params = mBandit(true_rewards,UCB,beta_params = estimated_beta_params) # 加载之前的内容
print(estimated_beta_params)
print(' second start. ...')
prob2 = BanditProbs(estimated_beta_params,topics,printf = True,plotf = True)
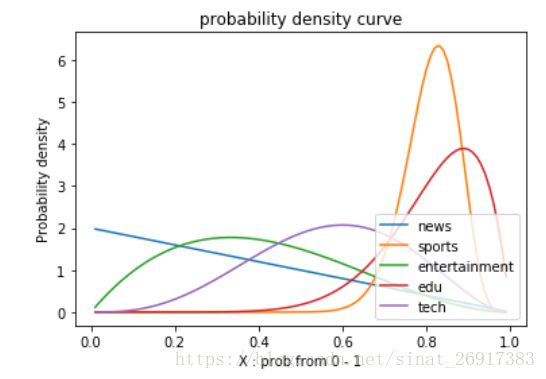
来看一张胡乱迭代了很多轮之后的图:
可以看到有两个高峰,是sports主题以及edu主题。
【news】 topic prob is : 0.01
【sports】 topic prob is : 0.8300000000000001
【entertainment】 topic prob is : 0.33
【edu】 topic prob is : 0.89
【tech】 topic prob is : 0.6
【参考】:
Bandit算法与推荐系统
bandit算法原理及Python实现
推荐系统的EE问题及Bandit算法