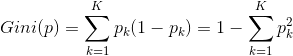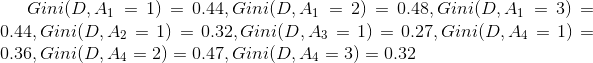决策树思想与Python实现：CART

一、决策树

决策树（decision tree）是一种基本的分类与回归方法。一般情况下，回归方法可以转换为分类方法，因此，本文主要讨论用于分类的决策树。

决策树在分类问题中，表示基于特征对实例进行分类的过程。主要优点是模型具有可读性，分类速度快。

决策树包含3个步骤：特征选择、决策树的生成、决策树的修剪。在此文中，只讨论前面两个步骤。

决策树学习的算法通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割，使得对各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分，也对应着决策树的构建。

开始，构建根结点，将所有训练数据都放在根结点。选择一个最优特征，按照这一特征将训练数据集分割成子集，使得各个子集有一个在当前条件下最好的分类。如果这些子集已经能够被基本正确分类，那么构建叶结点，并将这些子集分到所对应的叶结点中去；如果还有子集不能被基本正确分类，那么久对这些子集选择新的最优特征，继续对其进行分割，构建相应的节点。如此递归地进行下去，直至所有训练数据子集被基本正确分类，或者没有合适的特征为止。最后每个子集都被分到叶结点上，即都有了明确的类。这就生成了一棵决策树。

决策树主要算法有：ID3、C4.5、CART。以及进化后的C4.5算法C5.0、分类有极大提升的Tsallis等算法。这些算法的区别就在于选择最优特征的方式。但C5.0的核心原理与C4.5是相同的，它对于C4.5的改进在于计算速率，尤其是对于大数据，C4.5的速度非常慢，而C5.0对大数据运算效率极高。但C5.0一直是商用算法，未开源，但官方提供了可将C5.0构建的分类器嵌入到自己组织中的C源码。

对于CART算法，它是二类分类常用的方法，CART算法得到的一定是二叉树。

二、决策树之CART生成算法

以一个例子来逐步讲解CART算法：

下表示由15个样本组成的贷款申请训练数据。数据包括贷款申请人的4个特征（属性）：年龄（3个可能值：青年、中年、老年）、工作（2个可能值：是，否）、有自己的房子（2个可能值：是、否）、信贷情况（3个可能值：非常好、好、一般）。表的最后一列是类别，是否同意贷款：是、否。

贷款申请样本数据表

ID	年龄	有工作	有自己的房子	信贷情况	类别：同意贷款
1	青年	是	是	一般	是
2	青年	是	否	好	是
3	青年	否	否	好	否
4	青年	否	否	一般	否
5	青年	否	否	一般	否
6	中年	是	是	好	是
7	中年	否	是	非常好	是
8	中年	否	是	非常好	是
9	中年	否	否	好	否
10	中年	否	否	一般	否
11	老年	是	否	非常好	是
12	老年	是	否	好	是
13	老年	否	是	非常好	是
14	老年	否	是	好	是
15	老年	否	否	一般	否

希望通过所给的训练数据学习一个贷款申请的决策树，用以对未来的贷款申请进行分类，即当新的客户提出贷款申请时，根据申请人的特征，利用决策树决定是否批准贷款申请。

CART算法是通过基尼指数来选择最优特征的。

1.基尼指数

分类问题中，假设有K个类，样本点属于第k类的概率为pk，则概率分布的基尼指数定义为

 

由于CART只用于二类分类问题，则对于二类分类问题，若样本点属于第1个类的概率为p，那么概率分布的基尼指数为

对于给定的样本几何D，其基尼指数为

这里，Ck是D中属于第k类的样本子集，K是类的个数。

如果样本几何D根据特征A是否取某可能值a而被分割成D1和D2两部分，即

则在特征A的条件下，集合D的基尼指数定义为

基尼指数Gini(D)表示集合D的不确定性，基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性。因此，基尼指数值越大，样本集合的不确定性也就越大。也即是，基尼指数小的特征具有更强的分类能力。

2.计算基尼指数

在上面的例子中，分别以A1、A2、A3、A4表示年龄、有工作、有自己的房子和信贷情况4个特征，以1，2，3表示年龄的值为青年、中年和老年，以1，2表示有工作和有自己的房子的值为是和否，以1，2，3表示信贷情况的值为非常好，好喝一般。

则对于特征A1=1的基尼指数：它将年龄分为了青年和非青年（中年、老年），青年有5个样本，非青年有10个样本；在5个青年样本中，同意贷款的有2个样本，不同意贷款的有3个样本；在10个非青年样本中，同意贷款的有7个样本，不同意贷款的有3个样本，则根据上面集合D的基尼指数公式：

其中

则

类似地，可以求出其他基尼指数

对这些基尼指数分析，发现Gini(D,A3=1)=0.27最小，则选择特征A3位最优特征，A3=1为其最优切分点。则A3是否有自己的房子为根结点，左子树里为属性为是的样本集，右子树为属性为否的样本集。然后分别对剩余的特征继续计算最优特征。

在上面的4个特征中，第1、4个特征都有三个属性，因此它们都会各自产生三个基尼指数。例如上面显示的，当选定年龄的左子树为青年时，右子树为非青年；当选定年龄的左子树为中年时，右子树为非中年；当选定年龄的左子树为老年时，右子树为非老年。信贷情况类似。而对于第2、3特征，它们各自都只有两个属性，那么如果左子树是属性1，右子树必然是属性2；如果左子树是属性2，右子树必然是属性1。而左右子树的顺序对决策树的结果并没有影响，因此它们都只有一个基尼指数。

在上面的8个基尼指数中，出现了两个值相同的情况：Gini(D,A1=1)=Gini(D,A1=3)=0.44，如果它们是所有基尼系数中值最小的，那么最优切分点从它们中产生。此处它们都属于特征A1年龄，那么最优特征为年龄，最优切分点从这二者中随便选择一个即可。相似的， 如果Gini(D,A1=1)=Gini(D,A4=3)，且它们是所有基尼系数中值最小的，那么最优特征从它们各自对应的特征中产生，此时随便选择A1年龄或A4信贷情况都可以。

3.CART生成算法

CART算法的核心是在决策树各个节点上应用基尼指数准则选择特征。

输入：训练数据集D，停止计算的条件（可选）

输出：CART决策树

根据训练数据集，从根结点开始，递归地对每个结点进行以下操作，构建二叉决策树：

（1）计算现有特征对该数据集的基尼指数，如上面所示；

（2）选择基尼指数最小的值对应的特征为最优特征，对应的切分点为最优切分点（若最小值对应的特征或切分点有多个，随便取一个即可）；

（3）按照最优特征和最优切分点，从现结点生成两个子结点，将训练数据集中的数据按特征和属性分配到两个子结点中；

（4）对两个子结点递归地调用（1）（2）（3），直至满足停止条件。

（5）生成CART树。

算法停止的条件：结点中的样本个数小于预定阈值，或样本集的基尼指数小于预定阈值（样本基本属于同一类，如完全属于同一类则为0），或者特征集为空。

4.决策树的优化

一般情况下，决策树产生的树往往对训练数据的分类很准确，尤其是不设置阈值时。但当用于对未知数据分类时却没有那么准确，即出现过拟合现象。因为当分类过于细致，当一个属性不对应，那么就很可能出现不能分类的情况。

解决建立决策树时易发生过拟合现象的方法：剪枝、随机森林。

剪枝即是从已生成的树上裁减掉一些子树或者叶结点，并将其根结点或父结点作为新的叶结点。

随机森林是根据样本集和特征集，建立很多的决策树，每一棵树对于同一个未知数据都会有一个类别，统计这些类别，类别数最多的那个类即为未知数据的类别。

本文不讨论决策树优化的具体方法。

三、CART算法的Python实现

from math import log
import operator

def createDataSet1():
    """
    创造示例数据/读取数据
    @param dataSet: 数据集
    @return dataSet labels：数据集 特征集
    """
    # 数据集
    dataSet = [('青年', '否', '否', '一般', '不同意'),
               ('青年', '否', '否', '好', '不同意'),
               ('青年', '是', '否', '好', '同意'),
               ('青年', '是', '是', '一般', '同意'),
               ('青年', '否', '否', '一般', '不同意'),
               ('中年', '否', '否', '一般', '不同意'),
               ('中年', '否', '否', '好', '不同意'),
               ('中年', '是', '是', '好', '同意'),
               ('中年', '否', '是', '非常好', '同意'),
               ('中年', '否', '是', '非常好', '同意'),
               ('老年', '否', '是', '非常好', '同意'),
               ('老年', '否', '是', '好', '同意'),
               ('老年', '是', '否', '好', '同意'),
               ('老年', '是', '否', '非常好', '同意'),
               ('老年', '否', '否', '一般', '不同意')]
    # 特征集
    labels = ['年龄', '有工作', '有房子', '信贷情况']
    return dataSet,labels

def calcProbabilityEnt(dataSet):
    """
    样本点属于第1个类的概率p，即计算2p(1-p)中的p
    @param dataSet: 数据集
    @return probabilityEnt: 数据集的概率
    """
    numEntries = len(dataSet)  # 数据条数
    feaCounts = 0
    fea1 = dataSet[0][len(dataSet[0]) - 1]
    for featVec in dataSet:  # 每行数据
        if featVec[-1] == fea1:
            feaCounts += 1
    probabilityEnt = float(feaCounts) / numEntries
    return probabilityEnt

def splitDataSet(dataSet, index, value):
    """
    划分数据集，提取含有某个特征的某个属性的所有数据
    @param dataSet: 数据集
    @param index: 属性值所对应的特征列
    @param value: 某个属性值
    @return retDataSet: 含有某个特征的某个属性的数据集
    """
    retDataSet = []
    for featVec in dataSet:
        # 如果该样本该特征的属性值等于传入的属性值，则去掉该属性然后放入数据集中
        if featVec[index] == value:
            reducedFeatVec = featVec[:index] + featVec[index+1:] # 去掉该属性的当前样本
            retDataSet.append(reducedFeatVec) # append向末尾追加一个新元素，新元素在元素中格式不变，如数组作为一个值在元素中存在
    return retDataSet

def chooseBestFeatureToSplit(dataSet):
    """
    选择最优特征
    @param dataSet: 数据集
    @return bestFeature: 最优特征所在列
    """
    numFeatures = len(dataSet[0]) - 1 # 特征总数
    if numFeatures == 1:  # 当只有一个特征时
        return 0
    bestGini = 1  # 最佳基尼系数
    bestFeature = -1  # 最优特征
    for i in range(numFeatures):
        uniqueVals = set(example[i] for example in dataSet) # 去重，每个属性值唯一
        feaGini = 0 # 定义特征的值的基尼系数
        # 依次计算每个特征的值的熵
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet,i,value) # 根据该特征属性值分的类
                                                       # 参数：原数据、循环次数(当前属性值所在列)、当前属性值
            prob = len(subDataSet) / float(len(dataSet))
            probabilityEnt = calcProbabilityEnt(subDataSet)
            feaGini += prob * (2 * probabilityEnt * (1 - probabilityEnt))
        if (feaGini < bestGini):  # 基尼系数越小越好
            bestGini = feaGini
            bestFeature = i
    return bestFeature

def majorityCnt(classList):
    """
    对最后一个特征分类，出现次数最多的类即为该属性类别，比如：最后分类为2男1女，则判定为男
    @param classList: 数据集，也是类别集
    @return sortedClassCount[0][0]: 该属性的类别
    """
    classCount = {}
    # 计算每个类别出现次数
    for vote in classList:
        try:
            classCount[vote] += 1
        except KeyError:
            classCount[vote] = 1
    sortedClassCount = sorted(classCount.items(),key = operator.itemgetter(1),reverse = True) # 出现次数最多的类别在首位
                                                    # 对第1个参数，按照参数的第1个域来进行排序（第2个参数），然后反序（第3个参数）
    return sortedClassCount[0][0] # 该属性的类别

def createTree(dataSet,labels):
    """
    对最后一个特征分类，按分类后类别数量排序，比如：最后分类为2同意1不同意，则判定为同意
    @param dataSet: 数据集
    @param labels: 特征集
    @return myTree: 决策树
    """
    classList = [example[-1] for example in dataSet]  # 获取每行数据的最后一个值，即每行数据的类别
    # 当数据集只有一个类别
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    # 当数据集只剩一列（即类别），即根据最后一个特征分类
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    # 其他情况
    bestFeat = chooseBestFeatureToSplit(dataSet) # 选择最优特征（所在列）
    bestFeatLabel = labels[bestFeat] # 最优特征
    del(labels[bestFeat]) # 从特征集中删除当前最优特征
    uniqueVals = set(example[bestFeat] for example in dataSet) # 选出最优特征对应属性的唯一值
    myTree = {bestFeatLabel:{}} # 分类结果以字典形式保存
    for value in uniqueVals:
        subLabels = labels[:] # 深拷贝，拷贝后的值与原值无关（普通复制为浅拷贝，对原值或拷贝后的值的改变互相影响）
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels) # 递归调用创建决策树
    return myTree


if __name__ == '__main__':
    dataSet, labels = createDataSet1()  # 创造示列数据
    print(createTree(dataSet, labels))  # 输出决策树模型结果

 

ID3/C4.5的实现见决策树思想与Python实现：ID3/C4.5

以上理论知识来自《统计学方法》（李航）和网络，源代码来自网络Python实现的ID3算法，我做了一定修改。