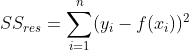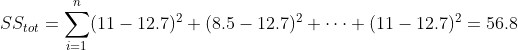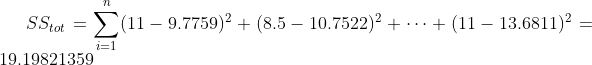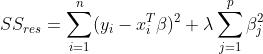机器学习系列:(二)线性回归
声明:版权所有,转载请联系作者并注明出处 http://blog.csdn.net/u013719780?viewmode=contents
博主简介:风雪夜归子(英文名: Allen),机器学习算法攻城狮,喜爱钻研Machine Learning的黑科技,对Deep Learning和Artificial Intelligence充满兴趣,经常关注kaggle数据挖掘竞赛平台,对数据、Machine Learning和Artificial Intelligence有兴趣的各位童鞋可以一起探讨哦,个人CSDN博客: http://blog.csdn.net/u013719780?viewmode=contents
线性回归
本章介绍用线性模型处理回归问题。从简单问题开始,先处理一个响应变量和一个解释变量的一元问题。然后,我们介绍多元线性回归问题(multiple linear regression),线性约束由多个解释变量构成。紧接着,我们介绍多项式回归分析(polynomial regression问题),一种具有非线性关系的多元线性回归问题。最后,我们介绍如果训练模型获取目标函数最小化的参数值。在研究一个大数据集问题之前,我们先从一个小问题开始学习建立模型和学习算法。
一元线性回归
上一章我们介绍过在监督学习问题中用训练数据来估计模型参数。训练数据由解释变量的历史观测值和对应的响应变量构成。模型可以预测不在训练数据中的解释变量对应的响应变量的值。回归问题的目标是预测出响应变量的连续值。本章我们将学习一些线性回归模型,后面会介绍训练数据,建模和学习算法,以及对每个方法的效果评估。首先,我们从简单的一元线性回归问题开始。
假设你想计算匹萨的价格。虽然看看菜单就知道了,不过也可以用机器学习方法建一个线性回归模型,通过分析匹萨的直径与价格的数据的线性关系,来预测任意直径匹萨的价格。我们先用scikit-learn写出回归模型,然后我们介绍模型的用法,以及将模型应用到具体问题中。假设我们查到了部分匹萨的直径与价格的数据,这就构成了训练数据,如下表所示:
| 训练样本 | 直径(英寸) | 价格(美元) |
|---|---|---|
| 1 | 6 | 7 |
| 2 | 8 | 9 |
| 3 | 10 | 13 |
| 4 | 14 | 17.5 |
| 5 | 18 | 18 |
我们可以用matplotlib画出图形:
%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\msyh.ttc", size=10)
def runplt():
plt.figure()
plt.title('匹萨价格与直径数据',fontproperties=font)
plt.xlabel('直径(英寸)',fontproperties=font)
plt.ylabel('价格(美元)',fontproperties=font)
plt.axis([0, 25, 0, 25])
plt.grid(True)
return plt
plt = runplt()
X = [[6], [8], [10], [14], [18]]
y = [[7], [9], [13], [17.5], [18]]
plt.plot(X, y, 'k.')
plt.show()
上图中,'x'轴表示匹萨直径,'y'轴表示匹萨价格。能够看出,匹萨价格与其直径正相关,这与我们的日常经验也比较吻合,自然是越大越贵。下面我们就用scikit-learn来构建模型。
from sklearn.linear_model import LinearRegression
# 创建并拟合模型
model = LinearRegression()
model.fit(X, y)
print('预测一张12英寸匹萨价格:$%.2f' % model.predict([12])[0])
一元线性回归假设解释变量和响应变量之间存在线性关系;这个线性模型所构成的空间是一个超平面(hyperplane)。超平面是n维欧氏空间中余维度等于一的线性子空间,如平面中的直线、空间中的平面等,总比包含它的空间少一维。在一元线性回归中,一个维度是响应变量,另一个维度是解释变量,总共两维。因此,其超平面只有一维,就是一条线。
上述代码中sklearn.linear_model.LinearRegression类是一个估计器(estimator)。估计器依据观测值来预测结果。在scikit-learn里面,所有的估计器都带有fit()和predict()方法。fit()用来分析模型参数,predict()是通过fit()算出的模型参数构成的模型,对解释变量进行预测获得的值。因为所有的估计器都有这两种方法,所有scikit-learn很容易实验不同的模型。
LinearRegression类的fit()方法学习下面的一元线性回归模型:
y=α+βx
y 表示响应变量的预测值,本例指匹萨价格预测值, x 是解释变量,本例指匹萨直径。截距 α 和相关系数 β 是线性回归模型最关心的事情。下图中的直线就是匹萨直径与价格的线性关系。用这个模型,你可以计算不同直径的价格,8英寸$7.33,20英寸$18.75。
plt = runplt()
plt.plot(X, y, 'k.')
X2 = [[0], [10], [14], [25]]
model = LinearRegression()
model.fit(X, y)
y2 = model.predict(X2)
plt.plot(X, y, 'k.')
plt.plot(X2, y2, 'g-')
plt.show()
一元线性回归拟合模型的参数估计常用方法是普通最小二乘法(ordinary least squares )或线性最小二乘法(linear least squares)。首先,我们定义出拟合成本函数,然后对参数进行数理统计。
带成本函数的模型拟合评估
下图是由若干参数生成的回归直线。如何判断哪一条直线才是最佳拟合呢?
plt = runplt()
plt.plot(X, y, 'k.')
y3 = [14.25, 14.25, 14.25, 14.25]
y4 = y2 * 0.5 + 5
model.fit(X[1:-1], y[1:-1])
y5 = model.predict(X2)
plt.plot(X, y, 'k.')
plt.plot(X2, y2, 'g-.')
plt.plot(X2, y3, 'r-.')
plt.plot(X2, y4, 'y-.')
plt.plot(X2, y5, 'o-')
plt.show()
成本函数(cost function)也叫损失函数(loss function),用来定义模型与观测值的误差。模型预测的价格与训练集数据的差异称为残差(residuals)或训练误差(training errors)。后面我们会用模型计算测试集,那时模型预测的价格与测试集数据的差异称为预测误差(prediction errors)或训练误差(test errors)。
模型的残差是训练样本点与线性回归模型的纵向距离,如下图所示:
plt = runplt()
plt.plot(X, y, 'k.')
X2 = [[0], [10], [14], [25]]
model = LinearRegression()
model.fit(X, y)
y2 = model.predict(X2)
plt.plot(X, y, 'k.')
plt.plot(X2, y2, 'g-')
# 残差预测值
yr = model.predict(X)
for idx, x in enumerate(X):
plt.plot([x, x], [y[idx], yr[idx]], 'r-')
plt.show()
import numpy as np
print('残差平方和: %.2f' % np.mean((model.predict(X) - y) ** 2))
有了成本函数,就要使其最小化获得参数。
解一元线性回归的最小二乘法
通过成本函数最小化获得参数,我们先求相关系数 β β。按照频率论的观点,我们首先需要计算 x x的方差和 x x与 y y的协方差。
方差是用来衡量样本分散程度的。如果样本全部相等,那么方差为0。方差越小,表示样本越集中,反正则样本越分散。方差计算公式如下:
var(x)=∑ni=1(xi−x¯)2n−1
其中, x¯ 是直径 x 的均值, xi 的训练集的第 i 个直径样本, n 是样本数量。计算如下:
# 如果是Python2,加from __future__ import division
xbar = (6 + 8 + 10 + 14 + 18) / 5
variance = ((6 - xbar)**2 + (8 - xbar)**2 + (10 - xbar)**2 + (14 - xbar)**2 + (18 - xbar)**2) / 4
print(variance)
Numpy里面有var方法可以直接计算方差,ddof参数是贝塞尔(无偏估计)校正系数(Bessel's correction),设置为1,可得样本方差无偏估计量。
print(np.var([6, 8, 10, 14, 18], ddof=1))
协方差表示两个变量的总体的变化趋势。如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。如果两个变量不相关,则协方差为0,变量线性无关不表示一定没有其他相关性。协方差公式如下:
cov(x,y)=∑ni=1(xi−x¯)(yi−y¯)n−1
其中, x¯ 是直径 x 的均值, xi 的训练集的第 i 个直径样本, y¯ 是价格 y 的均值, yi 的训练集的第 i 个价格样本, n 是样本数量。计算如下:
ybar = (7 + 9 + 13 + 17.5 + 18) / 5
cov = ((6 - xbar) * (7 - ybar) + (8 - xbar) * (9 - ybar) + (10 - xbar) * (13 - ybar) +
(14 - xbar) * (17.5 - ybar) + (18 - xbar) * (18 - ybar)) / 4
print(cov)
Numpy里面有cov方法可以直接计算方差。
import numpy as np
print(np.cov([6, 8, 10, 14, 18], [7, 9, 13, 17.5, 18])[0][1])
现在有了方差和协方差,就可以计算相关系统 β 了。
β=cov(x,y)var(x)
β=22.6523.2=0.9762931034482758
算出 β 后,我们就可以计算 α 了:
α=y¯−βx¯
将前面的数据带入公式就可以求出 α 了:
α=12.9−0.9762931034482758×11.2=1.9655172413793114
这样就通过最小化成本函数求出模型参数了。把匹萨直径带入方程就可以求出对应的价格了,如11英寸直径价格$12.70,18英寸直径价格$19.54。
模型评估
前面我们用学习算法对训练集进行估计,得出了模型的参数。如何评价模型在现实中的表现呢?现在让我们假设有另一组数据,作为测试集进行评估。
| 训练样本 | 直径(英寸) | 价格(美元) | 预测值(美元) |
|---|---|---|---|
| 1 | 8 | 11 | 9.7759 |
| 2 | 9 | 8.5 | 10.7522 |
| 3 | 11 | 15 | 12.7048 |
| 4 | 16 | 18 | 17.5863 |
| 5 | 12 | 11 | 13.6811 |
有些度量方法可以用来评估预测效果,我们用R方(r-squared)评估匹萨价格预测的效果。R方也叫确定系数(coefficient of determination),表示模型对现实数据拟合的程度。计算R方的方法有几种。一元线性回归中R方等于皮尔逊积矩相关系数(Pearson product moment correlation coefficient或Pearson's r)的平方。
这种方法计算的R方一定介于0~1之间的正数。其他计算方法,包括scikit-learn中的方法,不是用皮尔逊积矩相关系数的平方计算的,因此当模型拟合效果很差的时候R方会是负值。下面我们用scikit-learn方法来计算R方。
# 测试集
X_test = [[8], [9], [11], [16], [12]]
y_test = [[11], [8.5], [15], [18], [11]]
model = LinearRegression()
model.fit(X, y)
model.score(X_test, y_test)
多元线性回归
可以看出匹萨价格预测的模型R方值并不显著。如何改进呢?
回顾一下自己的生活经验,匹萨的价格其实还会受到其他因素的影响。比如,匹萨的价格还与上面的辅料有关。让我们再为模型增加一个解释变量。用一元线性回归已经无法解决了,我们可以用更具一般性的模型来表示,即多元线性回归。
y=α+β1x1+β2x2+⋯+βnxn
写成矩阵形式如下:
Y=Xβ
一元线性回归可以写成如下形式:
⎡⎣⎢⎢⎢⎢Y1Y2⋮Yn⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢α+βX1α+βX2⋮α+βXn⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢11⋮1X1X2⋮Xn⎤⎦⎥⎥⎥⎥×[αβ]
其中, Y 是训练集的响应变量列向量, β 是模型参数列向量。 X 称为设计矩阵,是 m×n 维训练集的解释变量矩阵。 m 是训练集样本数量, n 是解释变量个数。增加辅料的匹萨价格预测模型训练集如下表所示:
| 训练样本 | 直径(英寸) | 辅料种类 | 价格(美元) |
|---|---|---|---|
| 1 | 8 | 11 | 9.7759 |
| 2 | 9 | 8.5 | 10.7522 |
| 3 | 11 | 15 | 12.7048 |
| 4 | 16 | 18 | 17.5863 |
| 5 | 12 | 11 | 13.6811 |
我们同时要升级测试集数据:
| 测试样本 | 直径(英寸) | 辅料种类 | 价格(美元) |
|---|---|---|---|
| 1 | 8 | 2 | 11 |
| 2 | 9 | 0 | 8.5 |
| 3 | 11 | 2 | 15 |
| 4 | 16 | 2 | 18 |
| 5 | 12 | 0 | 11 |
我们的学习算法评估三个参数的值:两个相关因子和一个截距。 β β的求解方法可以通过矩阵运算来实现。
Y=Xβ
矩阵没有除法运算(详见线性代数相关内容),所以用矩阵的转置运算和逆运算来实现:
β=(XTX)−1XTY
通过Numpy的矩阵操作就可以完成:
from numpy.linalg import inv
from numpy import dot, transpose
X = [[1, 6, 2], [1, 8, 1], [1, 10, 0], [1, 14, 2], [1, 18, 0]]
y = [[7], [9], [13], [17.5], [18]]
print(dot(inv(dot(transpose(X), X)), dot(transpose(X), y)))
Numpy也提供了最小二乘法函数来实现这一过程:
from numpy.linalg import lstsq
print(lstsq(X, y)[0])
有了参数,我们就来更新价格预测模型:
from sklearn.linear_model import LinearRegression
X = [[6, 2], [8, 1], [10, 0], [14, 2], [18, 0]]
y = [[7], [9], [13], [17.5], [18]]
model = LinearRegression()
model.fit(X, y)
X_test = [[8, 2], [9, 0], [11, 2], [16, 2], [12, 0]]
y_test = [[11], [8.5], [15], [18], [11]]
predictions = model.predict(X_test)
for i, prediction in enumerate(predictions):
print('Predicted: %s, Target: %s' % (prediction, y_test[i]))
print('R-squared: %.2f' % model.score(X_test, y_test))
增加解释变量让模型拟合效果更好了。后面我们会论述一个问题:为什么只用一个测试集评估一个模型的效果是不准确的,如何通过将测试集数据分块的方法来测试,让模型的测试效果更可靠。不过现在我们可以认为,匹萨价格预测问题,多元回归确实比一元回归效果更好。假如解释变量和响应变量的关系不是线性的呢?下面我们来研究一个特别的多元线性回归的情况,可以用来构建非线性关系模型。
多项式回归
上例中,我们假设解释变量和响应变量的关系是线性的。真实情况未必如此。下面我们用多项式回归,一种特殊的多元线性回归方法,增加了指数项( x x的次数大于1)。现实世界中的曲线关系都是通过增加多项式实现的,其实现方式和多元线性回归类似。本例还用一个解释变量,匹萨直径。让我们用下面的数据对两种模型做个比较:
| 训练样本 | 直径(英寸) | 价格(美元) |
|---|---|---|
| 1 | 6 | 7 |
| 2 | 8 | 9 |
| 3 | 10 | 13 |
| 4 | 14 | 17.5 |
| 5 | 18 | 18 |
| 测试样本 | 直径(英寸) | 价格(美元) |
|---|---|---|
| 1 | 6 | 7 |
| 2 | 8 | 9 |
| 3 | 10 | 13 |
| 4 | 14 | 17.5 |
二次回归(Quadratic Regression),即回归方程有个二次项,公式如下:
y=α+β1x+β2x2
我们只用一个解释变量,但是模型有三项,通过第三项(二次项)来实现曲线关系。PolynomialFeatures转换器可以用来解决这个问题。代码如下:
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
X_train = [[6], [8], [10], [14], [18]]
y_train = [[7], [9], [13], [17.5], [18]]
X_test = [[6], [8], [11], [16]]
y_test = [[8], [12], [15], [18]]
regressor = LinearRegression()
regressor.fit(X_train, y_train)
xx = np.linspace(0, 26, 100)
yy = regressor.predict(xx.reshape(xx.shape[0], 1))
plt = runplt()
plt.plot(X_train, y_train, 'k.')
plt.plot(xx, yy)
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-')
plt.show()
print(X_train)
print(X_train_quadratic)
print(X_test)
print(X_test_quadratic)
print('一元线性回归 r-squared', regressor.score(X_test, y_test))
print('二次回归 r-squared', regressor_quadratic.score(X_test_quadratic, y_test))
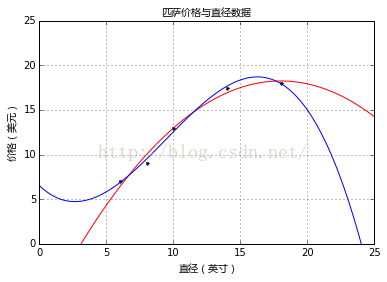
效果如上图所示,直线为一元线性回归(R方0.81),曲线为二次回归(R方0.87),其拟合效果更佳。还有三次回归,就是再增加一个立方项( β3x3 )。同样方法拟合,效果如下图所示:
plt = runplt()
plt.plot(X_train, y_train, 'k.')
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-')
cubic_featurizer = PolynomialFeatures(degree=3)
X_train_cubic = cubic_featurizer.fit_transform(X_train)
X_test_cubic = cubic_featurizer.transform(X_test)
regressor_cubic = LinearRegression()
regressor_cubic.fit(X_train_cubic, y_train)
xx_cubic = cubic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_cubic.predict(xx_cubic))
plt.show()
print(X_train_cubic)
print(X_test_cubic)
print('二次回归 r-squared', regressor_quadratic.score(X_test_quadratic, y_test))
print('三次回归 r-squared', regressor_cubic.score(X_test_cubic, y_test))
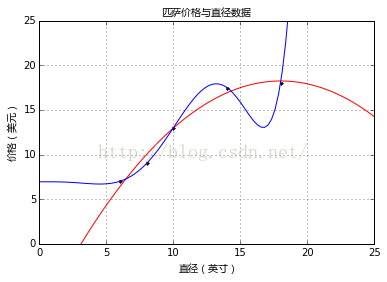
从图中可以看出,三次回归经过的点更多,但是R方值却没有二次回归高。下面我们再看一个更高阶的,七次回归,效果如下图所示:
plt = runplt()
plt.plot(X_train, y_train, 'k.')
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-')
seventh_featurizer = PolynomialFeatures(degree=7)
X_train_seventh = seventh_featurizer.fit_transform(X_train)
X_test_seventh = seventh_featurizer.transform(X_test)
regressor_seventh = LinearRegression()
regressor_seventh.fit(X_train_seventh, y_train)
xx_seventh = seventh_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_seventh.predict(xx_seventh))
plt.show()
print('二次回归 r-squared', regressor_quadratic.score(X_test_quadratic, y_test))
print('七次回归 r-squared', regressor_seventh.score(X_test_seventh, y_test))
可以看出,七次拟合的R方值更低,虽然其图形基本经过了所有的点。可以认为这是拟合过度(over-fitting)的情况。这种模型并没有从输入和输出中推导出一般的规律,而是记忆训练集的结果,这样在测试集的测试效果就不好了。
正则化
正则化(Regularization)是用来防止拟合过度的一堆方法。正则化向模型中增加信息,经常是一种对抗复杂性的手段。与奥卡姆剃刀原理(Occam's razor)所说的具有最少假设的论点是最好的观点类似。正则化就是用最简单的模型解释数据。
scikit-learn提供了一些方法来使线性回归模型正则化。其中之一是岭回归(Ridge Regression,RR,也叫Tikhonov regularization),通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法。岭回归增加L2范数项(相关系数向量平方和的平方根)来调整成本函数(残差平方和):
λ 是调整成本函数的超参数(hyperparameter),不能自动处理,需要手动调整一种参数。 λ 增大,成本函数就变大。
scikit-learn也提供了最小收缩和选择算子(Least absolute shrinkage and selection operator, LASSO),增加L1范数项(相关系数向量平方和的平方根)来调整成本函数(残差平方和):
LASSO方法会产生稀疏参数,大多数相关系数会变成0,模型只会保留一小部分特征。而岭回归还是会保留大多数尽可能小的相关系数。当两个变量相关时,LASSO方法会让其中一个变量的相关系数会变成0,而岭回归是将两个系数同时缩小。
scikit-learn还提供了弹性网(elastic net)正则化方法,通过线性组合L1和L2兼具LASSO和岭回归的内容。可以认为这两种方法是弹性网正则化的特例。
线性回归应用案例
前面我们通过一个小例子介绍了线性回归模型。下面我们用一个现实的数据集来应用线性回归算法。假如你去参加聚会,想喝最好的红酒,可以让朋友推荐,不过你觉得他们也不靠谱。作为科学控,你带了pH试纸和一堆测量工具来测酒的理化性质,然后选一个最好的,周围的小伙伴都无语了,你亮瞎了世界。
网上有相关的酒数据集可以参考,UCI机器学习项目的酒数据集收集了1599种酒的测试数据。收集完数据自然要用线性回归来研究一下,响应变量是0-10的整数值,我们也可以把这个问题看成是一个分类问题。不过本章还是把相应变量作为连续值来处理。
探索数据
scikit-learn作为机器学习系统,其探索数据的能力是不能与SPSS和R语言相媲美的。不过我们有Pandas库,可以方便的读取数据,完成描述性统计工作。我们通过描述性统计来设计模型。Pandas引入了R语言的dataframe,一种二维表格式异质(heterogeneous)数据结构。Pandas更多功能请见文档,这里只用一部分功能,都很容易使用。
首先,我们读取.csv文件生成dataframe:
import pandas as pd
df = pd.read_csv('mlslpic/winequality-red.csv', sep=';')
df.head()
Out[5]:
df.describe()
Out[6]:
就这么简单,我们通过Dataframe.describe()方法获得了一堆描述性统计结果。pd.read_csv()读取.csv文件。下面我们在用matplotlib看看,获得更直观的认识:
plt.scatter(df['alcohol'], df['quality'])
plt.xlabel('Alcohol')
plt.ylabel('Quality')
plt.title('酒精度(Alcohol)与品质( Quality)',fontproperties=font)
plt.show()
散点图显示酒精度(Alcohol)与品质有比较弱的正相关特性,整体呈左下-右上趋势,也就是说酒精度较高的酒具有较高的品质。挥发性酸度(volatile acidity)与品质呈现负相关特性:
plt.scatter(df['volatile acidity'], df['quality'])
plt.xlabel('Volatile Acidity')
plt.ylabel('Quality')
plt.title('挥发性酸度(volatile acidity)与品质( Quality)',fontproperties=font)
plt.show()
这些图都可以显示出响应变量与解释变量的相关性;让我们构建一个多元线性相关模型表述这些相关性。如何决定哪个变量应该在模型中?哪个可以不在?通过Dataframe.corr()计算两两的关联矩阵(correlation matrix)。关联矩阵进一步确认了酒精度与品质的正相关性,挥发性酸度与品质的负相关性。挥发性酸度越高,酒喝着就越向醋。总之,我们就假设好酒应该具有酒精度高、挥发性酸度低的特点,虽然这和品酒师的味觉可能不太一致。
拟合与评估模型
现在,我们把数据分成训练集和测试集,训练回归模型然后评估预测结果:
import pandas as pd
import matplotlib.pylab as plt
from sklearn.linear_model import LinearRegression
from sklearn.cross_validation import train_test_split
df = pd.read_csv('mlslpic/winequality-red.csv', sep=';')
X = df[list(df.columns)[:-1]]
y = df['quality']
X_train, X_test, y_train, y_test = train_test_split(X, y)
regressor = LinearRegression()
regressor.fit(X_train, y_train)
y_predictions = regressor.predict(X_test)
print('R-squared:', regressor.score(X_test, y_test))
开始和前面类似,加载数据,然后通过train_test_split把数据集分成训练集和测试集。两个分区的数据比例都可以通过参数设置。默认情况下,25%的数据被分配给测试集。最后,我们训练模型并用测试集测试。
R方值0.38表明38%的测试集数据都通过了测试。如果剩下的72%的数据被分到训练集,那效果就不一样了。我们可以用交叉检验的方法来实现一个更完善的效果评估。上一章我们介绍过这类方法,可以用来减少不同训练和测试数据集带来的变化。
from sklearn.cross_validation import cross_val_score
regressor = LinearRegression()
scores = cross_val_score(regressor, X, y, cv=5)
print(scores.mean(), scores)
这里cross_val_score函数可以帮助我们轻松实现交叉检验功能。cv参数将数据集分成了5份。每个分区都会轮流作为测试集使用。cross_val_score函数返回模拟器score方法的结果。R方结果是在0.13到0.37之间,均值0.29,是模拟器模拟出的结果,相比单个训练/测试集的效果要好。
让我们看看一些模型的预测品质与实际品质的图象显示结果:
plt.scatter(y_test, y_predictions)
plt.xlabel('实际品质',fontproperties=font)
plt.ylabel('预测品质',fontproperties=font)
plt.title('预测品质与实际品质',fontproperties=font)
plt.show()
和假设一致,预测品质很少和实际品质完全一致。由于绝大多数训练数据都是一般品质的酒,所以这个模型更适合预测一般质量的酒。
梯度下降法拟合模型
前面的内容都是通过最小化成本函数来计算参数的:
β=(XTX)−1XTY
这里 X 是解释变量矩阵,当变量很多(上万个)的时候, XTX 计算量会非常大。另外,如果 XTX 的行列式为0,即奇异矩阵,那么就无法求逆矩阵了。这里我们介绍另一种参数估计的方法,梯度下降法(gradient descent)。拟合的目标并没有变,我们还是用成本函数最小化来进行参数估计。
梯度下降法被比喻成一种方法,一个人蒙着眼睛去找从山坡到溪谷最深处的路。他看不到地形图,所以只能沿着最陡峭的方向一步一步往前走。每一步的大小与地势陡峭的程度成正比。如果地势很陡峭,他就走一大步,因为他相信他仍在高出,还没有错过溪谷的最低点。如果地势比较平坦,他就走一小步。这时如果再走大步,可能会与最低点失之交臂。如果真那样,他就需要改变方向,重新朝着溪谷的最低点前进。他就这样一步一步的走啊走,直到有一个点走不动了,因为路是平的了,于是他卸下眼罩,已经到了谷底深处,小龙女在等他。
通常,梯度下降算法是用来评估函数的局部最小值的。我们前面用的成本函数如下:
可以用梯度下降法来找出成本函数最小的模型参数值。梯度下降法会在每一步走完后,计算对应位置的导数,然后沿着梯度(变化最快的方向)相反的方向前进。总是垂直于等高线。
需要注意的是,梯度下降法来找出成本函数的局部最小值。一个三维凸(convex)函数所有点构成的图行像一个碗。碗底就是唯一局部最小值。非凸函数可能有若干个局部最小值,也就是说整个图形看着像是有多个波峰和波谷。梯度下降法只能保证找到的是局部最小值,并非全局最小值。残差平方和构成的成本函数是凸函数,所以梯度下降法可以找到全局最小值。
梯度下降法的一个重要超参数是步长(learning rate),用来控制蒙眼人步子的大小,就是下降幅度。如果步长足够小,那么成本函数每次迭代都会缩小,直到梯度下降法找到了最优参数为止。但是,步长缩小的过程中,计算的时间就会不断增加。如果步长太大,这个人可能会重复越过谷底,也就是梯度下降法可能在最优值附近摇摆不定。
如果按照每次迭代后用于更新模型参数的训练样本数量划分,有两种梯度下降法。批量梯度下降(Batch gradient descent)每次迭代都用所有训练样本。随机梯度下降(Stochastic gradient descent,SGD)每次迭代都用一个训练样本,这个训练样本是随机选择的。当训练样本较多的时候,随机梯度下降法比批量梯度下降法更快找到最优参数。批量梯度下降法一个训练集只能产生一个结果。而SGD每次运行都会产生不同的结果。SGD也可能找不到最小值,因为升级权重的时候只用一个训练样本。它的近似值通常足够接近最小值,尤其是处理残差平方和这类凸函数的时候。
下面我们用scikit-learn的SGDRegressor类来计算模型参数。它可以通过优化不同的成本函数来拟合线性模型,默认成本函数为残差平方和。本例中,我们用波士顿住房数据的13个解释变量来预测房屋价格:
import numpy as np
from sklearn.datasets import load_boston
from sklearn.linear_model import SGDRegressor
from sklearn.cross_validation import cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.cross_validation import train_test_split
data = load_boston()
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target)
scikit-learn加载数据集的方法很简单。首先我们用train_test_split分割训练集和测试集。
X_scaler = StandardScaler()
y_scaler = StandardScaler()
X_train = X_scaler.fit_transform(X_train)
y_train = y_scaler.fit_transform(y_train)
X_test = X_scaler.transform(X_test)
y_test = y_scaler.transform(y_test)
然后用StandardScaler做归一化处理,后面会介绍。最后我们用交叉验证方法完成训练和测试:
regressor = SGDRegressor(loss='squared_loss')
scores = cross_val_score(regressor, X_train, y_train, cv=5)
print('交叉验证R方值:', scores)
print('交叉验证R方均值:', np.mean(scores))
regressor.fit_transform(X_train, y_train)
print('测试集R方值:', regressor.score(X_test, y_test))
总结
本章我们介绍了三类线性回归模型。首先,通过匹萨价格预测的例子介绍了一元线性回归,一个解释变量和一个响应变量的线性拟合。然后,我们讨论了多元线性回归,具有更一般形式的若干解释变量和一个响应变量的问题。最后,我们讨论了多项式回归,一种特殊的多元线性模型,体系了解释变量和响应变量的非线性特征。这三种模型都是一般线性模型的具体形式,在第4章,从线性回归到逻辑回归(Logistic Regression)。
我们将残差平方差最小化为目标来估计模型参数。首先,通过解析方法求解,我们介绍了梯度下降法,一种可以有效估计带许多解释变量的模型参数的优化方法。这章里的案例都很简单,很容易建模。下一章,我们介绍处理不同类型的解释变量的方法,包括分类数据、文字、图像。