SciPy 基础
SciPy以NumPy为基础,提供了应用更加广泛的科学计算工具。
其在以下方面有着优秀的函数库:
1.线性代数
2.数值积分
3.插值
4.优化
5.随机数生成
6.信号处理
7.图像处理
8.其他
与NumPy一样,SciPy有着稳定,成熟,且应用广泛的数值运算库。
许多SciPy函数仅仅是给诸如LAPACK,BLAS这样的Fortran数值计算工业标准库提供了接口。
在本文中,我们仅仅讨论一些常用的函数和特性,不做深入讨论。
一·SciPy与NumPy
由于SciPy以NumPy为基础,那么import scipy的同时便import 了numpy库。
所以,我们经常在SciPy函数的初始化文件中看到如下代码:
# Import numpy symbols to scipy name space
from numpy import *
from numpy.random import rand, randn
from numpy.fft import fft, ifft
from numpy.lib.scimath import *
# Remove the linalg imported from numpy so that the scipy.linalg package can be
# imported.
del linalgscipy.optimize scipy.integrate scipy.stats
所以这些子库需要分别import,比如:
import scipy.optimize
from scipy.integrate import quadimport numpy as np二·统计子库 scipy.stats
scipy.stats的主要功能有以下几个方面:
1.数值随机变量对象(包括密度分布函数,累积分布函数,样本函数等)
2.一些估计方法
3.一些测试方法
随机变量与分布
考虑beta函数。
numpy 中提供了获取随机变量的样本的方法:
In [1]: import numpy as np
In [2]: np.random.beta(5, 5, size=3)
Out[2]: array([ 0.6167565 , 0.67994589, 0.32346476])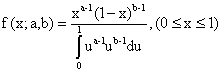
为了获取更多beta分布的特性,我们经常使用scipy.stats
import numpy as np
from scipy.stats import beta
from matplotlib.pyplot import hist, plot, show
q = beta(5, 5) # Beta(a, b), with a = b = 5 q是一个对象
obs = q.rvs(2000) # 2000 observations 获得2000个样本
hist(obs, bins=40, normed=True)
grid = np.linspace(0.01, 0.99, 100)
plot(grid, q.pdf(grid), 'k-', linewidth=2)
show()In [14]: q.cdf(0.4) # Cumulative distribution function 累积密度函数
Out[14]: 0.2665676800000002
In [15]: q.pdf(0.4) # Density function 密度函数
Out[15]: 2.0901888000000004
In [16]: q.ppf(0.8) # Quantile (inverse cdf) function
Out[16]: 0.63391348346427079
In [17]: q.mean()
Out[17]: 0.5identifier = scipy.stats.distribution_name(shape_parameters)distributon_name有两个关键参数loc和scale。
identifier = scipy.stats.distribution_name(shape_parameters, `loc=c`, `scale=d`)这里还有另一种方法生成与上一中方法一样的随机变量:
import numpy as np
from scipy.stats import beta
from matplotlib.pyplot import hist, plot, show
obs = beta.rvs(5, 5, size=2000) # 2000 observations
hist(obs, bins=40, normed=True)
grid = np.linspace(0.01, 0.99, 100)
plot(grid, beta.pdf(grid, 5, 5), 'k-', linewidth=2)
show()In [19]: from scipy.stats import linregress
In [20]: x = np.random.randn(200)
In [21]: y = 2 * x + 0.1 * np.random.randn(200)
In [22]: gradient, intercept, r_value, p_value, std_err = linregress(x, y)
In [23]: gradient, intercept
Out[23]: (1.9962554379482236, 0.008172822032671799)求根与稳定点:
稳定点:已知连续函数f(x) ,则函数f(x)的稳定点为x0,使得条件f(x0) = x0成立。
例如以下函数f(x):
如果我们要求方程f(x) = 0的根的化,可以利用scipy.optimize的二分法bisect。
n [24]: from scipy.optimize import bisect In [25]: f = lambda x: np.sin(4 * (x - 0.25)) + x + x**20 - 1 In [26]: bisect(f, 0, 1) Out[26]: 0.40829350427936706当然,在数值分析中还有一种常用方法Newton-Raphson算法。
这一方法利用函数曲线的切线 逐渐逼近零点。
如果函数的形态很好,那么此方法比bisect更快。
如果函数的形态不好,那么它比bisect慢。这主要是由于此方法依赖于求导运算。
在实际求根过程中,常常采用混合方法,先用一种方法求解,如果速度不快,则寻找
另外更好的方法,加速求解。
在SciPy中,混合方法是brentq:
from scipy.optimize import brentq
In [35]: brentq(f, 0, 1) Out[35]: 0.40829350427936706 In [36]: timeit brentq(f, 0, 1) 10000 loops, best of 3: 63.2 us per loop多元函数求根问题
常常采用 scipy.optimize.fsolve 一个MinPACK库接口。
移步http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fsolve.html 见真相
稳定点问题:
In [1]: from scipy.optimize import fixed_point In [2]: fixed_point(lambda x: x**2, 10.0) # 10.0 is an initial guess Out[2]: 1.0fixed_point函数仅仅限于一元函数固定点问题,因为它仅仅是调用了brentq函数。不要忘记,g(x)=f(x)-x 高中数学似乎总是有求不动点的题,我们这里就叫稳定点啦,一人一叫法。
优化问题
一元函数最小与最大值
In [9]: from scipy.optimize import fminbound In [10]: fminbound(lambda x: x**2, -1, 2) # Search in [-1, 2] Out[10]: 0.0多元函数最小与最大值
多元函数局部优化:有以下几个函数
minimize, fmin, fmin_powell, fmin_cg, fmin_bfgs, and fmin_ncg
多元函数受限局部优化:fmin_l_bfgs_b, fmin_tnc, fmin_cobyla
由于涉及更加多的搜索算法等数学知识就不详细介绍了。
具体问题请到官网:http://docs.scipy.org/doc/scipy/reference/optimize.html 查询
积分
单变量积分可以利用quad方法
In [13]: from scipy.integrate import quad In [14]: integral, error = quad(lambda x: x**2, 0, 1) In [15]: integral Out[15]: 0.33333333333333337quad方法是依靠gauss-chebyshev 求积公式,切比雪夫多项式参见:http://en.wikipedia.org/wiki/Clenshaw%E2%80%93Curtis_quadrature
多元函数积分,固定误差积分等可以参见:http://docs.scipy.org/doc/scipy/reference/integrate.html
图像操作
scipy的imread可以将图像导入numpy数组。
小猫在这里:
![]()
from scipy.misc import imread, imsave, imresize
# Read an JPEG image into a numpy array
img = imread('assets/cat.jpg')
print img.dtype, img.shape # Prints "uint8 (400, 248, 3)"
img_tinted = img * [1, 0.95, 0.9]
img_tinted = imresize(img_tinted, (300, 300))
将原来的array改变为正方形300*300pixels
![]()
彻彻底底变成了矮猫。
现在保存图像
imsave('assets/cat_tinted.jpg', img_tinted)创建三个点:
x = np.array([[0, 1], [1, 0], [2, 0]])这里的两点间距离用欧几里得空间的距离表示。
from scipy.spatial.distance import pdist, squareformd = squareform(pdist(x, 'euclidean'))[ 1.41421356 , 0. , 1. ],
[ 2.23606798 , 1. , 0. ]] 得到实对称矩阵。
而scipy.spatial.distance.cdist(A,B,'euclidean')计算的是两个array间各个点的欧几里得距离。
更加详细的方法可以参考:http://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.cdist.html