【数据结构】二叉树的遍历及应用

 

【fishing-pan：https://blog.csdn.net/u013921430转载请注明出处】

前言

      在二叉树的应用中，常常要求在树中查找某些结点，或者对树中的结点统一进行某种处理。因此，就提到了二叉树的遍历问题，对于线性结构来说，遍历是一个很容易解决的问题，而二叉树偏偏是一种非线性的结构，因此需要寻找一种规律。

       二叉树由三个基本单元组成，分别是根结点、左子树及右子树。依次遍历这三个部分就能遍历整个二叉树，以V、L、R表示访问根结点、遍历左子树及遍历右子树，则有VLR、VRL、RLV、RVL、LVR、LRV六种遍历二叉树的方案。若规定左子树一定先于右子树被遍历，就只剩下三种情况。再根据根结点被访问的次序，可以分为可以分别命名为先（根）序遍历，中（根）序遍历，后（根）序遍历。

        为了方便理解，定义一个二叉树的结点类型和二叉树类型；

template class BinaryTree;

template
class BinaryTreeNode
{
	friend class BinaryTree;
public:
	BinaryTreeNode();
	BinaryTreeNode(T D, BinaryTreeNode  *L=NULL, BinaryTreeNode  *R=NULL)
	{
		data = D;
		Lchild = L;
		Rchild = R;
	}

private:
	T data;
	BinaryTreeNode  *Lchild ;
	BinaryTreeNode  *Rchild ;

};

template
class BinaryTree
{
public:
	BinaryTree();
	BinaryTree(T D, BinaryTreeNode  *L=NULL, BinaryTreeNode  *R=NULL)
	{
		root = new BinaryTreeNode(D, L, R);
	}
	BinaryTree(BinaryTreeNode  *Node)
	{
		root = Node;
	}
	void PreOrder();
	void PreOrder(BinaryTreeNode  *current);

	void InOrder();
	void InOrder(BinaryTreeNode  *current);

	void PastOrder();
	void PastOrder(BinaryTreeNode  *current);
private:
	BinaryTreeNode  *root=NULL;
};

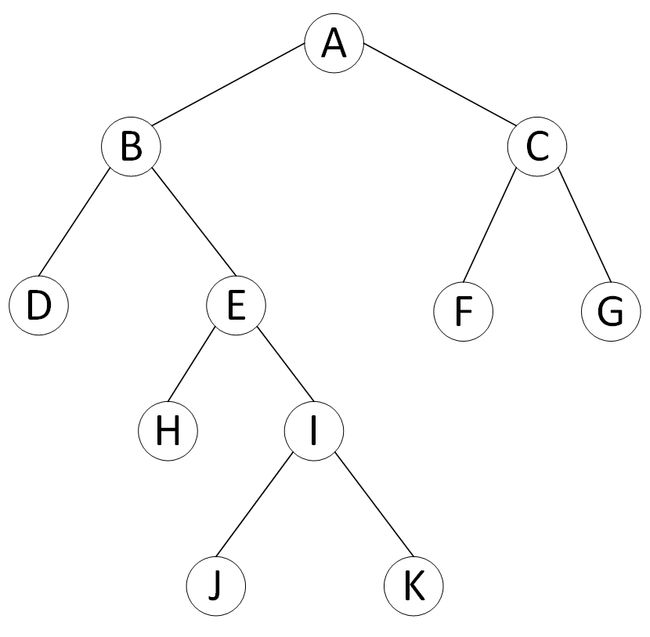
       构建一个如下图的二叉树；

 

二叉树的遍历

先序遍历

先序遍历的规则如下：若当前二叉树为空，则返回空，否则

1.  访问根结点；

2.  先序遍历左子树；

3.  先序遍历右子树；

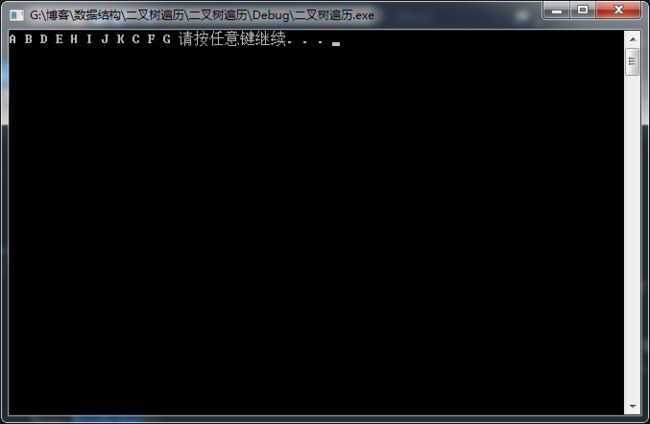
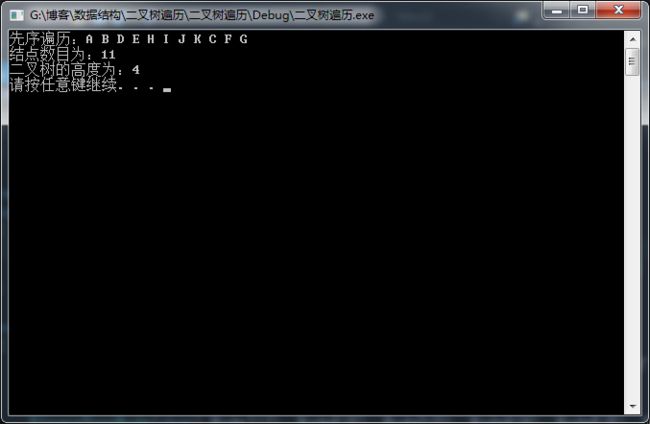
上图中的二叉树的先序遍历为：ABDEHIJKCFG

根据上面的关系，可以写出二叉树类的先序遍历的函数；

template
void BinaryTree::PreOrder()
{
	cout << "先序遍历：";
	PreOrder(root);        //先序遍历
}

template
void BinaryTree::PreOrder(BinaryTreeNode  *current)
{
	if (current != NULL)                   //当current为空指针，说明已经到达叶结点
	{
		cout << current->data<<" ";        //首先输出当前结点的值
		PreOrder(current->Lchild);         //递归调用左子树
		PreOrder(current->Rchild);         //递归调用右子树
	}
}

 

中序遍历

中序遍历的规则如下：若当前二叉树为空，则返回空，否则

1.  中序列根结点的左子树；

2.  访问根结点；

3.  中序遍历根结点的右子树；

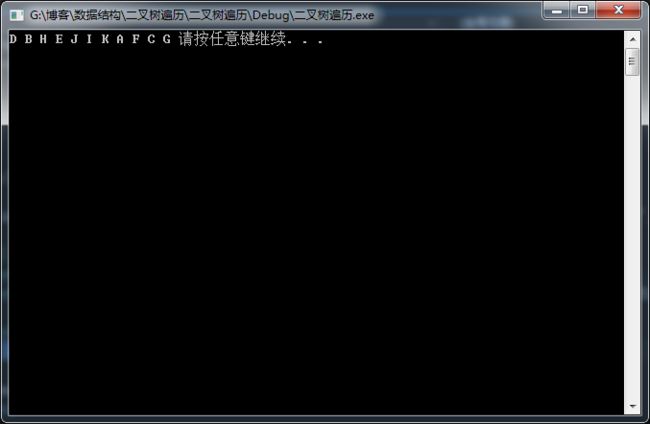
上图中的二叉树的中序遍历为：DBHEJIKAFCG

根据上面的关系，可以写出二叉树类的中序遍历的函数；

template
void BinaryTree::InOrder()
{
	InOrder(root);        //先序遍历
}

template
void BinaryTree::InOrder(BinaryTreeNode  *current)
{
	if (current != NULL)                   //当current为空指针，说明已经到达叶结点
	{
		
		InOrder(current->Lchild);         //递归调用左子树
		cout << current->data << " ";        //首先输出当前结点的值
		InOrder(current->Rchild);         //递归调用右子树
	}
}

 

后序遍历

后序遍历的规则如下：若当前二叉树为空，则返回空，否则

1.  后序列根结点的左子树；

2.  后序遍历根结点的右子树；

3.  访问根结点；

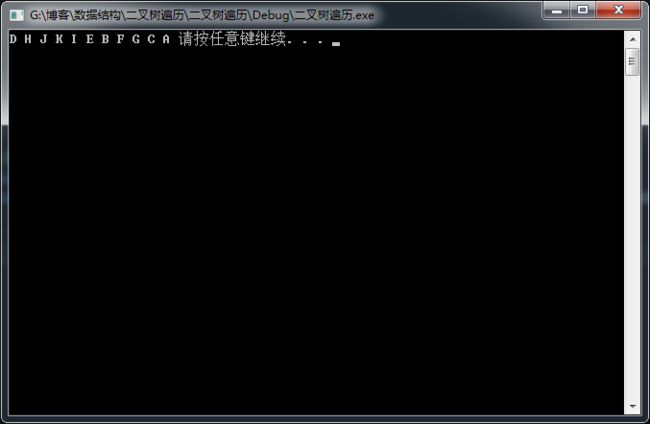
上图中的二叉树的后序遍历为：DHJKIEBFGCA

根据上面的关系，可以写出二叉树类的后序遍历的函数；

template
void BinaryTree::PastOrder()
{
	PastOrder(root);        //先序遍历
}

template
void BinaryTree::PastOrder(BinaryTreeNode  *current)
{
	if (current != NULL)                   //当current为空指针，说明已经到达叶结点
	{

		PastOrder(current->Lchild);         //递归调用左子树	
		PastOrder(current->Rchild);         //递归调用右子树
		cout << current->data << " ";        //首先输出当前结点的值
	}
}

 

二叉树遍历的应用

计算节点个数

      计算二叉树的节点的格式可以利用二叉树的遍历，常用的是后遍历，先遍历根结点的左子树和右子树，分别计算出左右子树的结点个数，然后加上根结点个数就是整个二叉树节点个数。

template
int BinaryTree::size(BinaryTreeNode  *current)
{
	if (current == NULL){ return 0; }
	else{ return 1 + size(current->Lchild) + size(current->Rchild); }
}

计算二叉树的高度

       与计算二叉树节点高度类似，计算二叉树高度时如果高度为0，返回-1；否则按照后序遍历规则，先递归计算根结点的左子树和右子树的高度，再求两者中的较大者，并加1，最终得到整个二叉树的高度；

template
int BinaryTree::depth(BinaryTreeNode  *current)
{
	if (current == NULL){ return -1; }
	else{ return 1 + Max(depth(current->Lchild), depth(current->Rchild)); }
}

知道先序（后序）和中序求二叉树后序（先序）

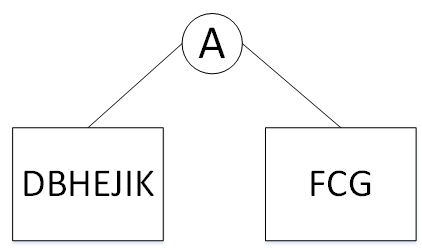
     有一些题目喜欢提这样的问题，以知道先序和中序求后序为例，例如已知先序是ABDEHIJKCFG，已知中序是DBHEJIKAFCG，求二叉树的后序排列。（知道先序和后序是无法求出中序的）

       其实了解二叉树的遍历后，这个题目很简单。由于先序是先遍历根结点，先序排列的第一个点必定根结点，也就是说A是根结点；再看中序遍历，先遍历左子树，左子树遍历玩才会遍历根结点，因此，排在A前方的全是左子树上的点，排在A后方的全是，如果A在中序排列中也是排在第一个，说明它没有左子树。因此有了如下结构；

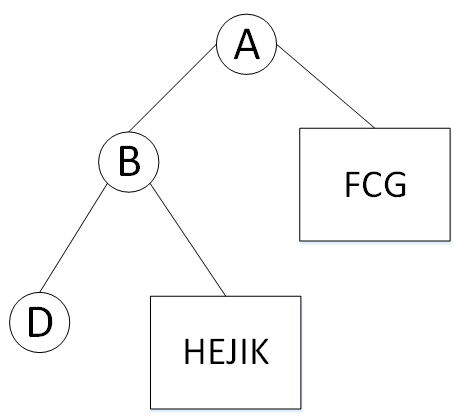
       再看左子树，此时左子树的先序为BDEHIJK，中序为DBHEJIK。同样的道理，B为A的左子树的根结点，中序排列中在B前面的为左子树，排在B后侧的为右子树；如此反复进行就能得出二叉树的结构，再进行后序遍历就能得出后序排列。

       当知道后序和中序排列求先序排列时，也是同样的道理，二叉树的根结点是最后被遍历到的点。

        根据上面的关系，可以的写出重建二叉树的函数；

template
BinaryTreeNode* BinaryTreeNode::reConstructBinaryTree(vector pre, vector in)
{
	BinaryTreeNode *BiTree=NULL;

	int size = pre.size();
	if (size != 0)
	{
		BiTree->data = pre[0];     //根结点赋值
		//构建左右子树的序列；
		vector leftPre;
		vector leftIn;
		vector rightPre;
		vector rightIn;

		//在中序排列中找到根结点的位置
		int i = 0;
		for (; ii)         //中序序列：排在根结点之后的放入右子树
			{

				rightIn.push_back(in[j]);
			}
		}
		for (int j = 1; j < size; j++)
		{
			if (j <= i)      //先序序列：排在根结点之前的放入左子树
			{
				leftPre.push_back(pre[j]);
			}
			if (j>i)         //先序序列：排在根结点之后的放入右子树
			{
				rightPre.push_back(pre[j]);
			}
		}
		if (leftIn.size() != 1){ BiTree->Lchild = reConstructBinaryTree(leftPre, leftIn); }
		if (rightIn.size() != 1){ BiTree->Rchild = reConstructBinaryTree(rightPre, rightIn); }
	}

	return BiTree;
}

最后

        二叉树的应用非常多，例如堆排序，二叉排序树，霍夫曼树等等，需要更多地去了解。

已完。