Inception v3 论文笔记

Inception v3：Rethinking the Inception Architecture for Computer Vision

摘要：
\quad    \; 卷积网络是大多数计算机视觉任务的 state of the art 模型采用的方法。自从2014年，VGG开始变为主流，在各种基准测试中有显著的性能提升。只要有足够的带标签数据，模型size和计算量的增加在大多数任务下能够提高性能，但计算的高效利用和更少的参数量使得在移动和大数据场景下的使用变得可能（模型size增加能带来性能提高，但计算量也会提高，所以计算量的高效利用和更少的参数成为了本文的研究目的）。在本文，作者通过分解卷积和aggressive正则 来探索能高效利用 随模型的增加而增加的计算量的模型scale方法（这句话有点绕）。作者在ILSVRRC 2012分类赛验证集上测试了新方法，并取得了取得了state of art（性能有了显著提高）：top-1: 21.2%，top-5: 5.6%的错误率for single frame evaluation。新方法每个inference的计算量为5 billion次乘-加运算，模型参数量不到25 million。4个模型进行集成并且进行multi-crop evaluation，新方法取得了top-1: 3.5%，top-5: 17.3%的错误率。

关键点：factorized convolution、aggressive regularization

1.简介

\quad    \; AlexNet使得深度学习开始被应用到各种任务。

\quad $;$2014年后，模型size的增大成为提高模型性能的主要研究方法（VGG、GoogLeNet）。尽管VGG取得了很好的性能，但它的计算量太大；GoogLeNet的Inception架构能够在strict constraints on memory and computational budget的情况下，取得很好的性能。另外GoogLeNet仅有5 million参数（1/12 AlexNet参数量）。VGG的参数量为AlexNet的3倍。

\quad    \; Inception的计算量比VGG少，但有更高性能。这使得能在大数据（inference时间要少）或移动环境（内存、计算力有限）的情景下使用Inception。

2.通用设计准则

• 1.避免representation瓶颈，尤其是网络前面的层。representation就是activations，activations的size应该是逐渐减减小的。
• 2.更高维的representation更容易处理，更容易训练（收敛）。
• 3.低维嵌入空间上的空间聚合（Spatial aggregation）几乎不会影响representation能力。这个的解释是相连神经元之间具有很强的相关性，信息有冗余。
• 4.网络宽度和深度的平衡。两者的平衡能带来更好的性能。

3.分解大filter size的卷积

\quad    \; GoogLeNet性能很大程度上来自于降维的广泛使用。例如，一个1x1卷积followed一个3x3卷积。在视觉任务中，我们希望临近的activations是高度相关的，所以，我们在aggregation之前降维。

\quad    \; 将大filter卷积分解为多个小filter卷积。这种分解能对参数进行解离。因此，训练速度会更快（with suitable factorization, we can end up with more disentangled parameters and therefore with faster training）。

3.1 分解为更小的卷积

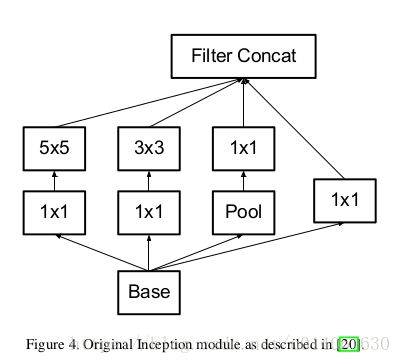
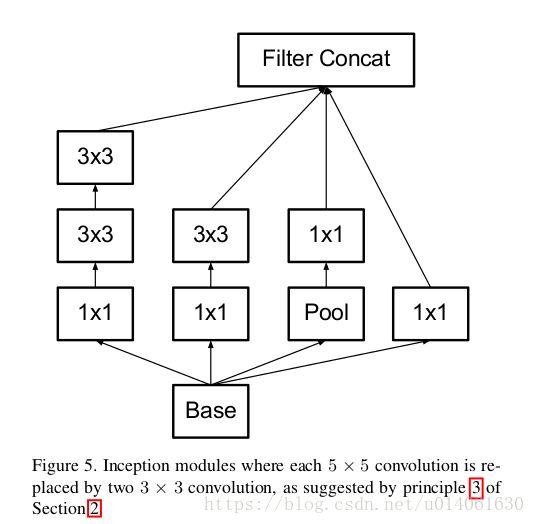
\quad    \; 将5x5分解为两个3x3，分解前和分解后的感受野是一样的。两个3x3卷积的串联比一个5x5卷积的representation能力更强。另外，分解后多使用了一个激活函数，增加了分线性能力（图2）。 两个3x3卷积和一个5x5卷积的参数量的比为$\frac{9+9}{25}$，分解减少了28%的参数。同时计算量也减少了28%。

\quad    \; 分解需要有两个需要注意的地方：1.分解是否会削弱representation能力；2.是否有必要在分解后的第一层后使用激活函数。

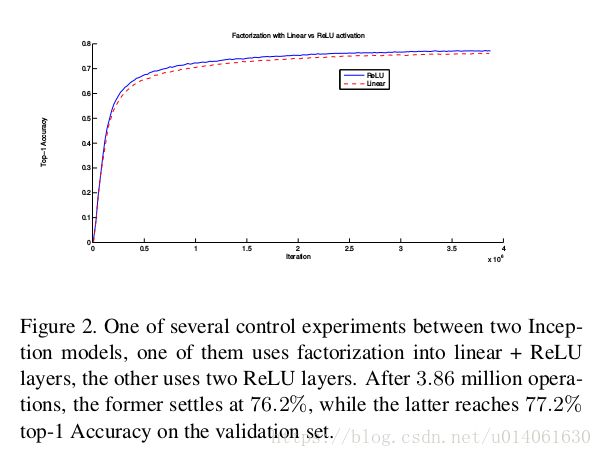
\quad    \; 分解不会降低representation能力，第一层后使用激活函数能增强非线性能力（图2）。分解是十分有好处的。所以原始的Inception模块（图4）就可以变为图5。

3.2 空间卷积分解为不对称卷积（Spatial Factorization into Asymmetric Convolutions）

\quad    \; 上一小节说明大filter的卷积层可以分解为一系列的3x3filter的卷积层。是否我们可以进一步分解为更小的filter的卷积层。事实上，通过卷积的非对称分解可以将3x3卷积分解为1x3和3x1卷积。在输入输出filters数目一定的时候，卷积的非对称分解可以将计算量减少33%。然而，如果将3x3卷积分解为两个2x2卷积只能减少11%的计算量。

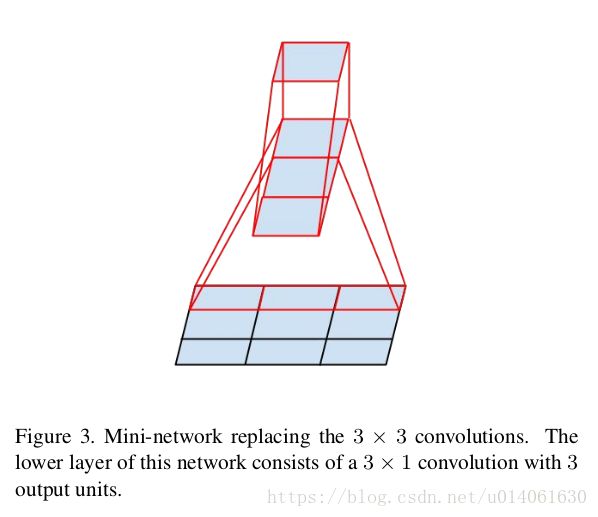
\quad    \; 理论上，**我们可以用1xn和nx1卷积的串联来代替nxn卷积，计算量可以可以降低为1/n。**实践中，非对称分解not work well on early layers，but it gives very good results on medium grid-sizes (On $mxm$ feature maps, 这里的$m$的范围为12到20)。在这种层面，very good results can be achieved by using 1x7 conv followed 7x1 conv。


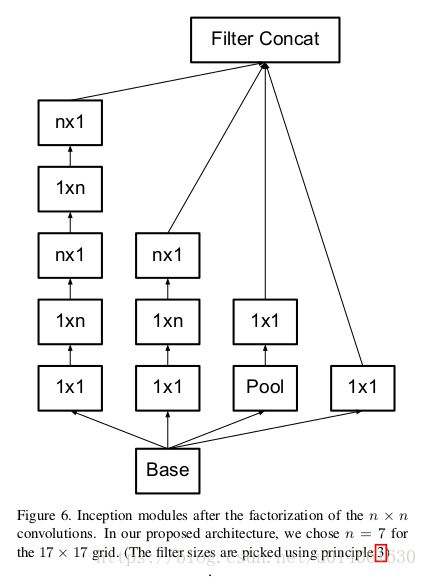
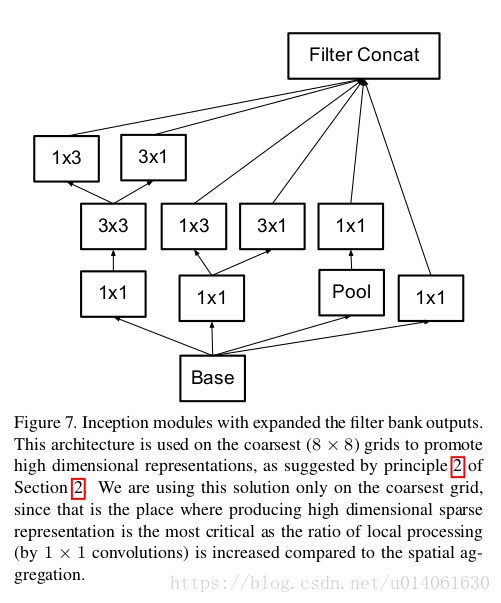
\quad    \; 根据设计准确2，高维表示更容易处理，更有利于训练，所以进行了图7的改造。

4. 辅助分类器的作用

\quad    \; Inception v1引进辅助的分类器去提高非常深的网络的收敛。引进辅助分类器的原始动机是加大梯度向更前层的流动（缓解梯度vanishing），从而加速训练过程中的收敛。Lee等人认为辅助分类器有助于更稳定的训练和better收敛。

\quad    \; 有趣的是，作者发现辅助分类器并不能加速训练过程的早期收敛：辅助分类器并没有加速网络的早期收敛。在训练末期，有辅助分类器的网络开始超越没有辅助分类器的模型的准确率。

\quad    \; Inception v1使用了两个辅助分类器。去掉低层辅助分类器并不会对网络的最终效果产生负面影响。结合上一段，这意味着Inception v1关于辅助分类器的假设（辅助分类器有助于低层特征的evolving）是错误的。取而代之，我们认为辅助分类器的作用是一个regularizer。作者关于上一句话的解释：如果辅助分类器进行BN或Dropout，网络的主分类器的性能会更好。这也间接说明（weak supporting evidence）了BN作为一个regularizer的推测。

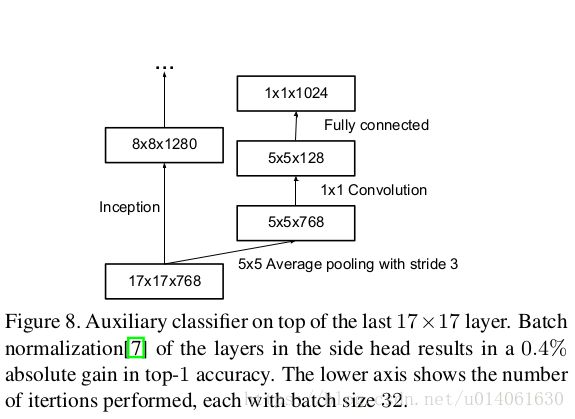
\quad    \; 通过上图，可以看出Inception v3的辅助分类器的配置。辅助分类器里的BN可以带来top-1: 0.4%的性能提升。

5. feature map的size的高效减小（Efficient Grid Size Reduction）

\quad    \; 一般来说，卷积神经网络使用一些pooling操作来减少grid size of the feature maps。为了避免representation瓶颈，在应用maximum或者average pooling之前需要将activation的维度进行增加。 例如，有一个$k$通道的$d\times d$的feature maps，如果我们想要得到一个$2k$通道的$\frac{d}{2}\times \frac{d}{2}$feature maps，我们首先需要去进行一个stride为1的$2k$个通道的卷积，然后另外应用一个pooling。

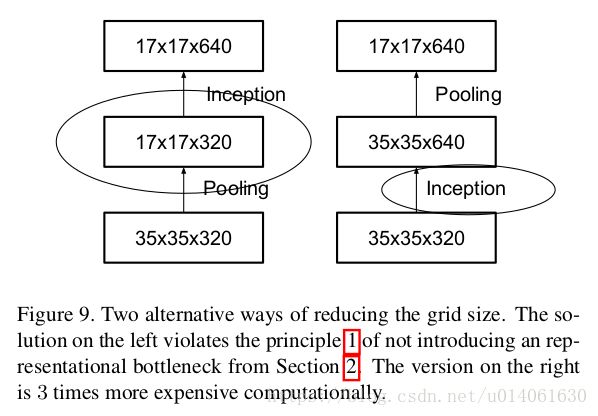
\quad    \; 左图缺点：带来了一个representation瓶颈
\quad    \; 右图缺点：计算量增加三倍

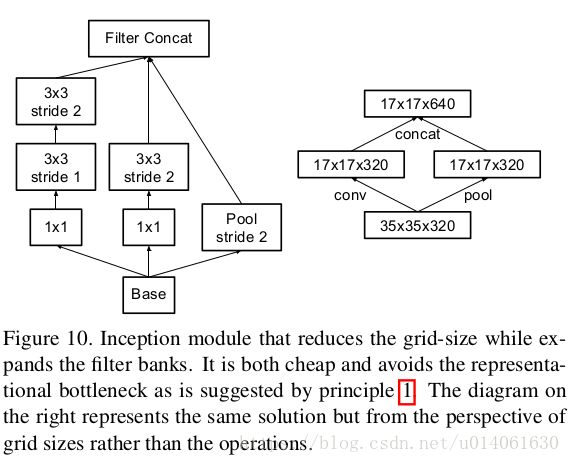
\quad    \; 右图是作者新提出的降低feature map的size的方法：用一个并行（conv + pooling两个path的stride都为2）来实现。它很cheap并且避免了representation瓶颈。从grid size而不是op的视角来看，右图represents the same solution。

6. Inception v2（这里作者其实指的是Inception v3）

\quad    \; 新Inception网络的配置如表1。

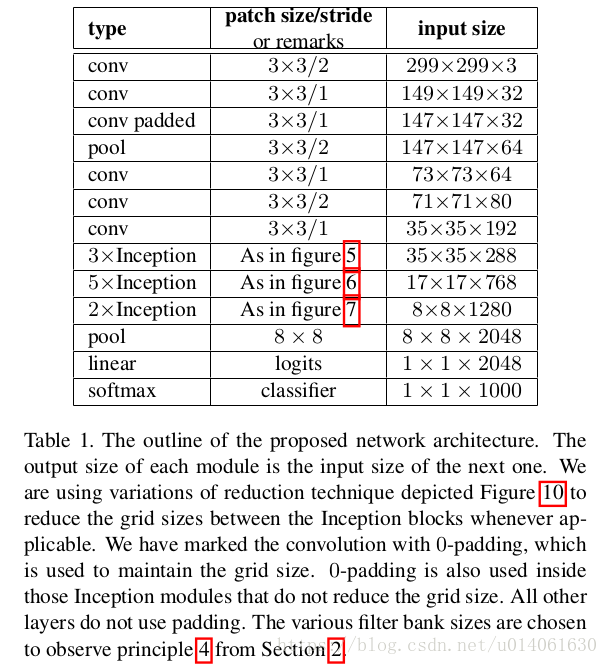
\quad    \; 注意，和Inception v2不同的是，作者将7x7卷积分解成了三个3x3卷积（这个分解在3.1节进行了描述）。网络中有三个Inception模组，三个模组的结构分别采用 图5、6、7三种结构。inception模块中的gird size reduction方法采用的是图10结构。

\quad    \; 我们可以看到，网络的质量与第二节说的准则有很大关系。尽管我们的网络深达42层，但我们的计算量仅仅是GoogLeNet的2.5倍，并且，它比VGG更高效。

7. Label Smoothing模型正则（Model Regularization via Label Smoothing）

\quad    \; 作者提出了一个正则分类器的机制：消除训练过程中label-dropout的边缘效应。

\quad    \; 对于每一个训练example $x$，模型计算每个label $k\in \{1...K\}$的概率：$p(k|x)=\frac{exp(z_k)}{{\sum }_{i=1}^{K}exp(z_i)}$，其中$z_i$是logits或未归一化的对数概率。

\quad    \; 训练集上单个example标签的实际概率分布（ground-truth distribution）经过归一化后：${\sum }_{k}q(k|x)=1$。为了简洁，我们忽略$p$和$q$对$x$的依赖。我们定义单个example上的cross entropy为$l=-{\sum }_{k=1}^{K}log(p(k))q(k)$。最小化cross entropy等价于最大化一个标签的对数极大似然值的期望（expected log-likelihood of a label），这里标签是根据$q(k)$选择的。cross entropy损失函数关于logits $z_k$是处处可微的，因此可以使用梯度下降来训练深度网络。其梯度有一个相当简单的形式：$\frac{\partial l}{\partial z_k}=p(k)-q(k)$，它的范围是在-1～1之间。

\quad    \; 对于一个真实的标签$y$：对于所有的$k̸=y$的情况，要$q(y)=1$并且$q(y)=1$。在这种情况下，最小化交叉熵等价于最大化正确标签的对数似然。对于一个标签为$y$的example $x$，最大化$q(k)={\delta }_{k,y}$时的对数似然，这里${\delta }_{k,y}$是狄拉克$\delta$函数。在$k=y$时，狄拉克函数等于1，其余等于0。通过训练，正确logit的$z_y$应该远大于其它$z_k$（$z̸=y$），$z_y$越大越好，但大是一个无终点的事情。这能够导致两个问题，1.导致过拟合：如果模型学习去将所有的概率分配到真实标签的逻辑单元上，泛化是没有保证的。2.它鼓励最大logit和其它logit的差异（KL距离）越大越好，结合有界梯度（dounded gradient）$\frac{\partial l}{\partial z_k}$，这降低了模型的适应能力。直觉上，适应能力的降低的原因应该是模型对它的预测太过于自信。

\quad    \; 作者提出了一个鼓励模型不过于自信的机制。如果目标是最大化训练标签的对数似然，那么这可能不是我们想要的，它对模型进行了正则并且使得模型的适应性更强。该方法是非常简单的。考虑一个独立于训练example $x$的标签分布$u(k)$，和一个smoothing参数$ϵ$。对于一个训练标签为$y$的example，我们替代标签分布$q(k|x)={\delta }_{k,y}$为：$$q^{\prime }(k|x)=(1-ϵ){\delta }_{k,y}+ϵu(k)$$新的分布是原始标签分布和一个指定分布$u(k)$的混合，两部分的权重为$1-ϵ$和$ϵ$。这可以看做标签$k$的分布是通过如下方式获得的：首先，set it to the ground-truth lable $k=y$；然后，以权重$ϵ$，replace $k$ with a sample drown from the distribution $u(k)$。作者建议去使用标签的先验分布作为$u(k)$。在我们的实验中，我们使用了均匀分布（$u(k)=1/K$）$$q^{\prime }(k)=(1-ϵ){\delta }_{k,y}+\frac{ϵ}{K}$$我们将这种改变ground-truth label分布的方法称为$label-smoothingregulariation$或者$LSR$。

\quad    \; 注意LSR达到了期望的目标：阻止最大的logit远大于其它logit。事实上，如果这发生了，则$q(k)$将接近1，而其它将接近0。这将导致一个很大的cross-entropy with $q^{\prime }(k)$，因为，不同于$q(k)={\delta }_{k,y}$，所有的$q^{\prime }(k)$有一个正的下界（positive lower bound）。

\quad    \; LSR的另一种损失函数可以通过研究交叉熵损失函数来获得$$H(q^{\prime },p)=-\sum _{k=1}^K\text{log }p(k)q^{\prime }(k)=(1-ϵ)H(q,p)+ϵH(u,p)$$ \quad    \; 因此，LSR等价于用一对损失函数$H(q,p)$和$H(u,p)$来代替单个损失函数$H(q,p)$。损失函数的第二项惩罚了预测标签的分布和先验分布$u$的偏差with相对权重$\frac{ϵ}{1-ϵ}$。注意，因为$H(u,p)=D_{KL}(u||p)+H(u)$，所以该偏差可以被KL散度捕获。当$u$是均匀分布的时候，$H(u,p)$衡量的是预测分布$p$和均匀分布之间的相似性，该相似性可以用负熵$-H(p)$来衡量，但两者并不相等。作者没有对这一替代进行研究。

\quad    \; 在 ImageNet 中 ，因为有1000类，所以作者令$K=1000$。故$u(k)=1/1000$，$ϵ=0.1$。对于ILSVRC2012，作者发现label-smoothing regularization可以将top-1和top-5准确率提高0.2%。

8. 训练方法

训练方法：TensorFlow里的随机梯度下降
设备：50片NV显卡
batch size：32
epochs：100
momentum：0.9
最后的模型的训练方法：RMSProp with decay 0.9 and $ϵ$ =1.0
学习速率：0.045 decayed every two epochs using an exponential rate of 0.94
另外，作者使用了梯度裁剪，裁剪的阈值：2.0，作者发现这十分有利于训练的稳定。
评估方法：对训练过程中不同时刻的参数的模型进行集成，取模型预测值的平均作为预测。

9. 在低分辨率输入情况下的性能

\quad    \; 研究分辨率的影响是为了搞清楚：高分辨率是否有助于性能的提升，能提高多少？

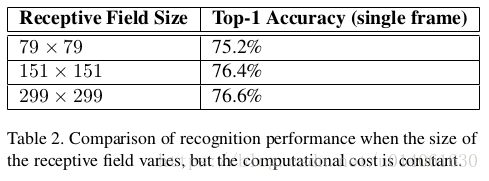
\quad    \; 这一部分，作者采用了三种分辨率的图像作为输入。三种情况的计算量是相同的。

\quad    \; 从表2可以看出，虽然低分辨率网络的训练时间更长，但最终的结果却和高分辨率网络相差无几。

\quad    \; 但是，如果我们根据输入分辨率，简单地减少网络尺寸，那么网络性能将明显下降。（困难任务上使用简单模型，性能肯定下降）

\quad    \; 表2的结果表明，我们应该考虑使用专用的high-cost 低分辨率网络for小物体in R-CNN中。

10. 实验中的结果和对比

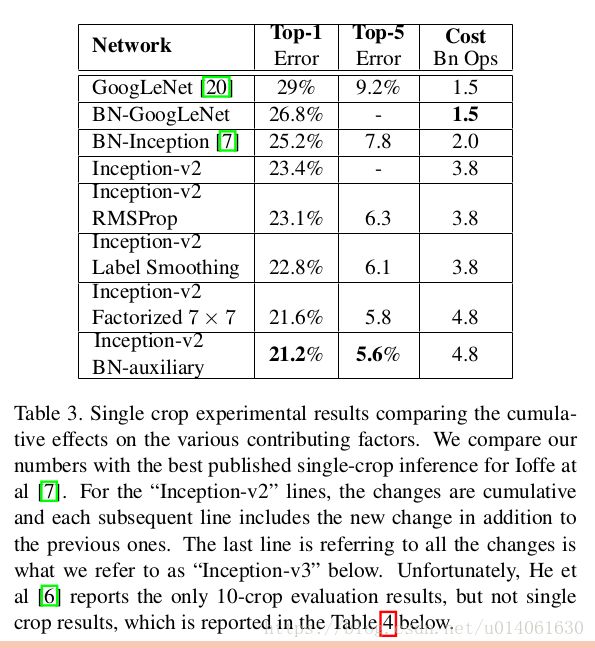
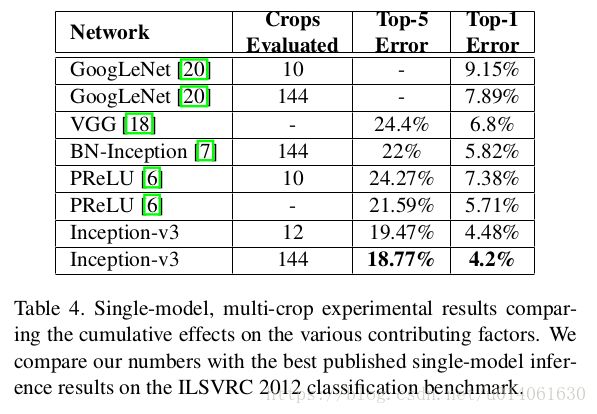
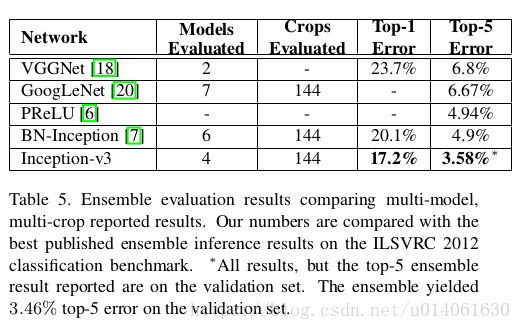
\quad    \; Inception v2在这里被称为BN-Inception，Inception v3取得了top-1: 17.2%，top-5:3.58%的错误率。

11.结论

\quad    \; 作者提出了几条扩大网络规模的设计准则，并在Inception背景下对它们进行了研究。从而产生了计算量不大却高性能的Inception v3。Inception v3的计算量相比v1提高了2.5倍。并且作者表明，低输入分辨率的情况下也可以达到近乎高分辨率输入的准确率。这可能有助于小物体的探测。降低参数量、附加BN或Dropout的辅助分类器、label-smoothing三大技术可以训练出高质量的网络（适当的训练集）

TensorFlow实现文章说的新的三种Inception结构5、6、7，同时给出原始的4：

#coding:utf-8
'''
Inception module
'''

import tensorflow as tf


def inception4(inputs, 
              sub_chs,
              stride, 
              is_training,
              scope='inception'):
  '''
  Figure 4
  
  sub_ch1: 1x1
  sub_ch2: 1x1  > 3x3
  sub_ch3: 1x1  > 5x5
  sub_ch4: pool > 1x1

  '''
  x = inputs
  [sub_ch1, sub_ch2, sub_ch3, sub_ch4] = sub_chs
  sub = []
  
  # 1x1
  sub1 = tf.layers.Conv2D(sub_ch1, [1,1], stride, padding='SAME')(x)
  sub1 = tf.layers.BatchNormalization()(sub1, training=is_training)
  sub1 = tf.nn.relu(sub1)
  sub.append(sub1)
  
  # 1x1 > 3x3
  sub2 = tf.layers.Conv2D(sub_ch2[0], [1,1], padding='SAME')(x)
  sub2 = tf.layers.BatchNormalization()(sub2, training=is_training)
  sub2 = tf.nn.relu(sub2)
  sub2 = tf.layers.Conv2D(sub_ch2[1], [3,3], stride, padding='SAME')(sub2)
  sub2 = tf.layers.BatchNormalization()(sub2, training=is_training)
  sub2 = tf.nn.relu(sub2)
  sub.append(sub2)
  
  # 1x1 > 5x5
  sub3 = tf.layers.Conv2D(sub_ch3[0], [1,1], padding='SAME')(x)
  sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
  sub3 = tf.nn.relu(sub3)
  sub3 = tf.layers.Conv2D(sub_ch3[1], [5,5], stride, padding='SAME')(sub3)
  sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
  sub3 = tf.nn.relu(sub3)
  sub.append(sub3)
  
  # pool > 1x1
  if sub_ch4[1] == None:
    if sub_ch4[0] == 'max':
      sub4 = tf.layers.MaxPooling2D([3,3], stride, padding='SAME')(x)
    elif sub_ch4[0] == 'avg':
      sub4 = tf.layers.AveragePooling2D([3,3], stride, padding='SAME')(x)
    else:
      raise ValueError
  else:
    if sub_ch4[0] == 'max':
      sub4 = tf.layers.MaxPooling2D([3,3], 1, padding='SAME')(x)
    elif sub_ch4[0] == 'avg':
      sub4 = tf.layers.AveragePooling2D([3,3], 1, padding='SAME')(x)
    else:
      raise ValueError
    sub4 = tf.layers.Conv2D(sub_ch4[1], [1,1], stride, padding='SAME')(sub4)
    sub4 = tf.layers.BatchNormalization()(sub4, training=is_training)
    sub4 = tf.nn.relu(sub4)
  sub.append(sub4)
  
  x = tf.concat(sub, axis=-1)
  return x


def inception5(inputs, 
              sub_chs,
              stride, 
              is_training,
              scope='inception'):
  '''
  Figure 5
  
  sub_ch1: 1x1
  sub_ch2: 1x1  > 3x3
  sub_ch3: 1x1  > 3x3 > 3x3
  sub_ch4: pool > 1x1

  '''
  x = inputs
  [sub_ch1, sub_ch2, sub_ch3, sub_ch4] = sub_chs
  sub = []
  
  # 1x1
  sub1 = tf.layers.Conv2D(sub_ch1, [1,1], stride, padding='SAME')(x)
  sub1 = tf.layers.BatchNormalization()(sub1, training=is_training)
  sub1 = tf.nn.relu(sub1)
  sub.append(sub1)
  
  # 1x1 > 3x3
  sub2 = tf.layers.Conv2D(sub_ch2[0], [1,1], padding='SAME')(x)
  sub2 = tf.layers.BatchNormalization()(sub2, training=is_training)
  sub2 = tf.nn.relu(sub2)
  sub2 = tf.layers.Conv2D(sub_ch2[1], [3,3], stride, padding='SAME')(sub2)
  sub2 = tf.layers.BatchNormalization()(sub2, training=is_training)
  sub2 = tf.nn.relu(sub2)
  sub.append(sub2)
  
  # 1x1  > 3x3 > 3x3
  sub3 = tf.layers.Conv2D(sub_ch3[0], [1,1], padding='SAME')(x)
  sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
  sub3 = tf.nn.relu(sub3)
  sub3 = tf.layers.Conv2D(sub_ch3[1], [3,3], 1, padding='SAME')(sub3)
  sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
  sub3 = tf.nn.relu(sub3)
  sub3 = tf.layers.Conv2D(sub_ch3[1], [3,3], stride, padding='SAME')(sub3)
  sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
  sub3 = tf.nn.relu(sub3)
  sub.append(sub3)
  
  # pool > 1x1
  if sub_ch4[1] == None:
    if sub_ch4[0] == 'max':
      sub4 = tf.layers.MaxPooling2D([3,3], stride, padding='SAME')(x)
    elif sub_ch4[0] == 'avg':
      sub4 = tf.layers.AveragePooling2D([3,3], stride, padding='SAME')(x)
    else:
      raise ValueError
  else:
    if sub_ch4[0] == 'max':
      sub4 = tf.layers.MaxPooling2D([3,3], 1, padding='SAME')(x)
    elif sub_ch4[0] == 'avg':
      sub4 = tf.layers.AveragePooling2D([3,3], 1, padding='SAME')(x)
    else:
      raise ValueError
    sub4 = tf.layers.Conv2D(sub_ch4[1], [1,1], stride, padding='SAME')(sub4)
    sub4 = tf.layers.BatchNormalization()(sub4, training=is_training)
    sub4 = tf.nn.relu(sub4)
  sub.append(sub4)
  
  x = tf.concat(sub, axis=-1)
  return x

def inception6(inputs,
               n,
               sub_chs,
               stride, 
               is_training,
               scope='inception'):
  '''
  Figure 6
  
  sub_ch1: 1x1
  sub_ch2: 1x1  > 1xn > nx1
  sub_ch3: 1x1  > 1xn > nx1 > 1xn > nx1
  sub_ch4: pool > 1x1

  '''
  x = inputs
  [sub_ch1, sub_ch2, sub_ch3, sub_ch4] = sub_chs
  sub = []
  
  # 1x1
  sub1 = tf.layers.Conv2D(sub_ch1, [1,1], stride, padding='SAME')(x)
  sub1 = tf.layers.BatchNormalization()(sub1, training=is_training)
  sub1 = tf.nn.relu(sub1)
  sub.append(sub1)
  
  # 1x1 > 1xn > nx1
  sub2 = tf.layers.Conv2D(sub_ch2[0], [1,1], padding='SAME')(x)
  sub2 = tf.layers.BatchNormalization()(sub2, training=is_training)
  sub2 = tf.nn.relu(sub2)
  sub2 = tf.layers.Conv2D(sub_ch2[1], [1,n], padding='SAME')(sub2)
  sub2 = tf.layers.BatchNormalization()(sub2, training=is_training)
  sub2 = tf.nn.relu(sub2)
  sub2 = tf.layers.Conv2D(sub_ch2[1], [n,1], stride, padding='SAME')(sub2)
  sub2 = tf.layers.BatchNormalization()(sub2, training=is_training)
  sub2 = tf.nn.relu(sub2)
  sub.append(sub2)
  
  # 1x1  > 1xn > nx1 > 1xn > nx1
  sub3 = tf.layers.Conv2D(sub_ch3[0], [1,1], padding='SAME')(x)
  sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
  sub3 = tf.nn.relu(sub3)
  sub3 = tf.layers.Conv2D(sub_ch3[1], [1,n], padding='SAME')(sub3)
  sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
  sub3 = tf.nn.relu(sub3)
  sub3 = tf.layers.Conv2D(sub_ch3[1], [n,1], padding='SAME')(sub3)
  sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
  sub3 = tf.nn.relu(sub3)
  sub3 = tf.layers.Conv2D(sub_ch3[1], [1,n], padding='SAME')(sub3)
  sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
  sub3 = tf.nn.relu(sub3)
  sub3 = tf.layers.Conv2D(sub_ch3[1], [n,1], stride, padding='SAME')(sub3)
  sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
  sub3 = tf.nn.relu(sub3)
  sub.append(sub3)
  
  # pool > 1x1
  if sub_ch4[1] == None:
    if sub_ch4[0] == 'max':
      sub4 = tf.layers.MaxPooling2D([3,3], stride, padding='SAME')(x)
    elif sub_ch4[0] == 'avg':
      sub4 = tf.layers.AveragePooling2D([3,3], stride, padding='SAME')(x)
    else:
      raise ValueError
  else:
    if sub_ch4[0] == 'max':
      sub4 = tf.layers.MaxPooling2D([3,3], 1, padding='SAME')(x)
    elif sub_ch4[0] == 'avg':
      sub4 = tf.layers.AveragePooling2D([3,3], 1, padding='SAME')(x)
    else:
      raise ValueError
    sub4 = tf.layers.Conv2D(sub_ch4[1], [1,1], stride, padding='SAME')(sub4)
    sub4 = tf.layers.BatchNormalization()(sub4, training=is_training)
    sub4 = tf.nn.relu(sub4)
  sub.append(sub4)
  
  x = tf.concat(sub, axis=-1)
  return x


def inception7(inputs, 
               sub_chs,
               stride, 
               is_training,
               scope='inception'):
  '''
  Figure 7
  
  sub_ch1: 1x1
  sub_ch2: 1x1  > 3x3
  sub_ch3: 1x1  > 3x3 > 3x3
  sub_ch4: pool > 1x1

  '''
  x = inputs
  [sub_ch1, sub_ch2, sub_ch3, sub_ch4] = sub_chs
  sub = []
  
  # 1x1
  sub1 = tf.layers.Conv2D(sub_ch1, [1,1], stride, padding='SAME')(x)
  sub1 = tf.layers.BatchNormalization()(sub1, training=is_training)
  sub1 = tf.nn.relu(sub1)
  sub.append(sub1)
  
  # 1x1 > 1x3 and 3x1
  sub2 = tf.layers.Conv2D(sub_ch2[0], [1,1], padding='SAME')(x)
  sub2 = tf.layers.BatchNormalization()(sub2, training=is_training)
  sub2 = tf.nn.relu(sub2)
  sub21 = tf.layers.Conv2D(sub_ch2[1], [1,3], stride, padding='SAME')(sub2)
  sub21 = tf.layers.BatchNormalization()(sub21, training=is_training)
  sub21 = tf.nn.relu(sub21)
  sub.append(sub21)
  sub22 = tf.layers.Conv2D(sub_ch2[1], [3,1], stride, padding='SAME')(sub2)
  sub22 = tf.layers.BatchNormalization()(sub22, training=is_training)
  sub22 = tf.nn.relu(sub22)
  sub.append(sub22)
  
  # 1x1  > 3x3 > 1x3 and 3x1
  sub3 = tf.layers.Conv2D(sub_ch3[0], [1,1], padding='SAME')(x)
  sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
  sub3 = tf.nn.relu(sub3)
  sub3 = tf.layers.Conv2D(sub_ch3[1], [3,3], 1, padding='SAME')(sub3)
  sub3 = tf.layers.BatchNormalization()(sub3, training=is_training)
  sub3 = tf.nn.relu(sub3)
  sub31 = tf.layers.Conv2D(sub_ch3[1], [1,3], stride, padding='SAME')(sub3)
  sub31 = tf.layers.BatchNormalization()(sub31, training=is_training)
  sub31 = tf.nn.relu(sub31)
  sub.append(sub31)
  sub32 = tf.layers.Conv2D(sub_ch3[1], [1,3], stride, padding='SAME')(sub3)
  sub32 = tf.layers.BatchNormalization()(sub31, training=is_training)
  sub32 = tf.nn.relu(sub32)
  sub.append(sub32)
  
  # pool > 1x1
  if sub_ch4[1] == None:
    if sub_ch4[0] == 'max':
      sub4 = tf.layers.MaxPooling2D([3,3], stride, padding='SAME')(x)
    elif sub_ch4[0] == 'avg':
      sub4 = tf.layers.AveragePooling2D([3,3], stride, padding='SAME')(x)
    else:
      raise ValueError
  else:
    if sub_ch4[0] == 'max':
      sub4 = tf.layers.MaxPooling2D([3,3], 1, padding='SAME')(x)
    elif sub_ch4[0] == 'avg':
      sub4 = tf.layers.AveragePooling2D([3,3], 1, padding='SAME')(x)
    else:
      raise ValueError
    sub4 = tf.layers.Conv2D(sub_ch4[1], [1,1], stride, padding='SAME')(sub4)
    sub4 = tf.layers.BatchNormalization()(sub4, training=is_training)
    sub4 = tf.nn.relu(sub4)
  sub.append(sub4)
  
  x = tf.concat(sub, axis=-1)
  return x


def aux_classifier(inputs):
  '''
  Figure 8
  '''
  x = inputs
  x = tf.layers.AveragePooling2D([5,5], 3)(x)
  x = tf.layers.Conv2D(128, [1,1])(x)
  x = tf.layers.Conv2D(1024, [5,5])(x)
  logits = tf.layers.Conv2D(1000, [1,1])(x)
  return logits


if __name__ == '__main__':
  x = tf.placeholder(tf.float32, [192, 28, 28, 3])
  y4 = inception4(x, [64, [96,128], [16,32], ['max',32]], 2, is_training=True, scope='1')
  y5 = inception5(x, [64, [96,128], [16,32], ['max',32]], 2, is_training=True, scope='1')
  y6 = inception6(x, 3, [64, [96,128], [16,32], ['max',32]], 2, is_training=True, scope='1')
  y7 = inception7(x, [64, [96,128], [16,32], ['max',32]], 2, is_training=True, scope='1')