曲线拐点快速寻找算法+C代码
定理 :
记关于平面上两点 P1(x1 ,y1) 和 P2(x2 ,y2)的正向直线方程L的左端表达式为函数
S12 (x , y)= (x2-x1)(y-y1) + (y1-y2)(x-x1)对于不在直线L上的任何一点 P0 (x0,y0 ) ,有
(1) 如果 S12 (x0,y0) <0 , 则 P0 (x0,y0 ) 是正向直线L的内点.;
(2) 如果 S12 (x0,y0) >0 , 则 P0 (x0,y0 ) 是正向直线L的外点。
对于不在同一直线上的三点可以确定此段曲线的凹凸性,而要获得曲线拐点信息至少需要四个点。
假设 P1(x1 ,y1), P2(x2 ,y2), P3(x3 ,y3) 和 P4(x4 ,y4)是曲线上相继的彼此很接近的4个点,且点P3(x3 ,y3)可能是拐点。
取 P1(x1 ,y1) 和 P2(x2 ,y2), 得到正向直线方程
L1 : S12(x, y) =0
计算函数值 S12 (x3, y3), 可以确定点 P3(x3 ,y3) 位于得到正向直线方程L1的哪一侧,然后再取点 P2(x2 ,y2), P3(x3,y3) 得到另一正向直线方程
L2 : S23 (x, y) =0
计算函数值S23 (x4, y4), 可以确定点P4(x4 ,y4) 位于得到正向直线方程L2的哪一侧。
如果S12 (x3, y3)*S23 (x4, y4) <0,可以得出点 P3(x3 ,y3) 是一个拐点,否则P3(x3 ,y3) 不是拐点。
重复上述计算步骤,即可判断 P3, P4, P5, ......, Pn-1 是否为拐点。
c语言代码如下:
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
struct point
{
double x;
double y;
};
point p[200];
double fun(point p1, point p2, point p3); //正向直线方程
void getPoint(); //获取测试点
void main()
{
int i, j;
getPoint();
double s1, s2;
for(i=3; i<199; i++)
{
s1 = fun(p[i-2], p[i-1], p[i]);
s2 = fun(p[i-1], p[i], p[i+1]);
if(s1*s2<0)
printf(" %lf %lf\n", p[i].x, p[i].y);
}
}
//正向直线方程
double fun(point p1, point p2, point p3)
{
double s;
s= (p2.x-p1.x)*(p3.y-p1.y)+(p1.y-p2.y)*(p3.x-p1.x);
return s;
}
//获取测试点
void getPoint()
{
double i;
int j=0;
for(i=0; i<7; i+=0.035)
{
p[j].x = i;
p[j].y = sin(i);
j++;
}
}
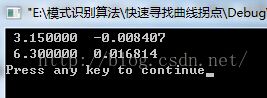
运行结果:
从结果中我们可以看出,函数 f=sinx,x=[0, 7];在PI 和 2*PI 处存在拐点。