模式识别hw3-------常见模式识别算法用于人脸图片性别识别
仍然感谢助教和队友,本文承接http://blog.csdn.net/bizer_csdn/article/details/54755843
实验平台为Matlab,并需要一些开源工具包
本次作业共采用了5种方法,其对应实验结果如下:
| vgg+PCA+LDA+SVM |
AdaBoost+LBP+LDA |
LBP\Fisherface+KNN |
SIFT特征点+PCA+SVM |
SIFT特征点+随机森林 |
| 91.70% |
94.80% |
89.80% |
69.1% |
76.30% |
目录
一、vgg网络
(1) 加载vgg网络
(2) PCA降维
(3) LDA降维
(4) 训练SVM分类器。
(5) 检验测试集
二、AdaBoost算法
(1) LBP提取特征
(2) PCA、LDA降维
三、LBP\Fisherface+KNN
(1) Fisher准则函数
(2) Fisherface方法
(3) knnRecognition
(4) 实验结果
四、SIFT特征点
(1) SIFT+PCA+LDA+SVM
(2) SIFT+随机森林
五、总结
一、vgg网络
本方法首先运用vgg网络提取人脸特征(4096维),然后在此基础上,用PCA、LDA和SVM的方法,对人脸图片进行识别。
vgg是一个37层用于人脸识别,并且已经训练好的网络,输出为“softmax”,把第36层输出的4096维向量作为输入人脸图片提取的特征,然后在此基础上运用传统模式对图片进行分类。
计算流程:
(1)加载vgg网络
加载vgg网络,vgg网络输入为 224*224*3的彩色图,而本次作业的图片是 灰度图,所以对于每张训练图片,要通过“imresize”后变为 ,然后减去vgg网络训练数据的均值(RGB每个通道都有),至此,输入格式也变为 ;然后通过“vl_simplenn”计算训练集中每个人脸图片的输出的4096维特征(每张人脸在输入网络前,必须进行去均值操作)。相关神经网络在上次作业中已经阐释,这里不再赘述。
load data\\train_data
train_num = size(tr_data,3);
% 用vgg网络提取特征特征(4096维),把特征存储在train_block(600*4096)中
% 读取vgg网络
net_path=fullfile(vl_rootnn, 'data', 'models','vgg-face.mat') ;
net=load(net_path);
train_block=zeros(train_num,4096);
for i=1:train_num/200
im=single(tr_data(:,:,i));
%让输入人脸图片符合vgg网络输入大小
im=imresize(im, net.meta.normalization.imageSize(1:2));
%去均值
im= bsxfun(@minus,im,net.meta.normalization.averageImage) ;
res = vl_simplenn(net, im) ;
%提取4096维向量
train_block(i,:)=res(end-2).x;
end
save data\\train_block;
(2)PCA降维
通过Matlab内置的“pca”函数对所提取的特征进行降维,当协方差所对应的特征值占据总能量的98%以上时候,将所对应的特征向量组成投影矩阵。简单介绍一下“pca”函数,用法如下所示:
[coeff,score,latent] =pca(train_block);
函数输入train_block对应训练样本集合,是一个 的矩阵,其中 是样本个数, 是样本维数;PCA实际上是求取一个投影变换矩阵,使得样本投影后尽可能地保留最大有用信息。
为求得投影矩阵,首先求取train_block的协方差矩阵,Matlab中是自动进行去均值操作的,而协方差矩阵为:
latent是对于特征值(按从大到小排序)。
%pca降维
[coeff,score,latent] = pca(train_block);
dim = 150;
while sum(latent(1:dim))/sum(latent) < 0.98
dim = dim + 1;
end
feature = score(:,1:dim);
(3)LDA降维
把经过PCA降维后的数据经过LDA再次降维。LDA是一种有监督的方法,它是通过Fisher准则求得投影矩阵,即
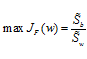
上式中,分母表示总的内类离散度, 分子表示类间的离散度,为了让投影后,各类更易于区分,目标就是最大化上式,而助教提供的函数“Lda”就是求得这个最佳投影矩阵。利用助教提供的lda函数,可进行lda变换
%lda
w = Lda(feature',tr_label);
feature = (w'*feature')';
(4)训练SVM分类器
训练SVM分类器,实际就是找一个最优分类面。性别分类是对应最简单的二分类,目标是找到分类器。 而所谓“支持向量(support vectors)”只是训练样本中很少一部分,这些支持向量更接近希望求得的分类面,并且也只有支持向量决定分类面。libSVM中函数“svmtrain”完成此计算步骤,示例%训练svm
model = svmtrain(tr_label',feature,'-s 0 -t 0');
(5)检验测试集
对于测试集中数据,仍然要通过vgg网络(仍需去均值),每张人脸图像得到4096维特征向量,然后把这些特征再次去训练集中的均值后,通过PCA计算得到的投影矩阵进行第一次降维,再通过LDA计算的投影矩阵,进行第二次降维,最后利用libSVM中“svmpredict”进行预测。示例代码:
load data\\test_block;
test_score = bsxfun(@minus,test_block,mean(train_block,1))*coeff;
test_feature = test_score(:,1:dim);
test_feature = (w'*test_feature')';
[predicted_label,accuracy,~] = svmpredict(te_label',test_feature,model);
最后结果,如下所示:

相比于助教提供的直接利用PCA、LDA、SVM正确率达到95.0943%的方法,这里精度并没有上述好,可能原因是vgg网络要求输入的是 224*224*3的彩色图,而作业训练数据是100*100 灰度图,最后每张图片同样被提取成4096维的特征向量,这一步可能造成精度丢失。
二、AdaBoost算法
AdaBoost是通过弱分类器组合达到较好效果,在一个迭代过程对分类器的输入和输出进行加权处理。

GML AdaBoostMatlab Toolbox提供了AdaBoost算法函数,里面内置了“Real AdaBoost”、“GentleAdaBoost”和“Modest AdaBoost”三种算法,内部弱分类器使用的是CART(Classification and Regression Trees)决策树。并且类别标签需要设置为 。其中,RealAdaBoost是最基本算法,后面两种算法效果更好。需要注意的是,函数“tree_node_w(max_splits)”输入的决策树在训练过程中最大分支数(树深)。示例如下:
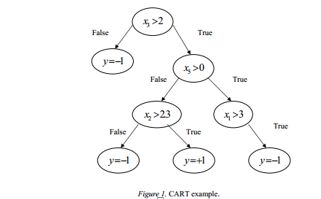
首先通过LBP算法提取特征,这里用的每张人脸图像经过LBP后,统计其均匀模式下灰度直方作为统计特征,即一个256维度(8阶灰度,共 )向量。
(1)LBP提取特征
load data\\train_data
train_num = size(tr_data,3);
%工具包要求类别标签设置为+1(男),-1(女);
tr_label(301:end)=-1;
%提取LBP特征
train_lbp=zeros(train_num,256);
for i=1:train_num
current = tr_data(:,:,i);
SP=[-1 -1; -1 0; -1 1; 0 -1; -0 1; 1 -1; 1 0; 1 1];
train_lbp(i,:) = lbp(current,SP,0,'h');
end
load data\\val_data
val_num = size(val_data,3);
%工具包要求类别标签设置为+1(男),-1(女);
val_label(81:end)=-1;
%提取LBP特征
val_lbp=zeros(val_num,256);
for i=1:val_num
current = val_data(:,:,i);
SP=[-1 -1; -1 0; -1 1; 0 -1; -0 1; 1 -1; 1 0; 1 1];
val_lbp(i,:) = lbp(current,SP,0,'h');
end
load data\\test_data
test_num = size(te_data,3);
%工具包要求类别标签设置为+1(男),-1(女);
te_label(210:end)=-1;
%提取LBP特征
test_lbp=zeros(test_num,256);
for i=1:test_num
current = te_data(:,:,i);
SP=[-1 -1; -1 0; -1 1; 0 -1; -0 1; 1 -1; 1 0; 1 1];
test_lbp(i,:) = lbp(current,SP,0,'h');
end
%通过训练集和验证集测试确定模型
MaxIter = 200; % boosting iterations
% and initializing matrices for storing step error
RAB_control_error = zeros(1, MaxIter);
MAB_control_error = zeros(1, MaxIter);
GAB_control_error = zeros(1, MaxIter);而测试集的结果:
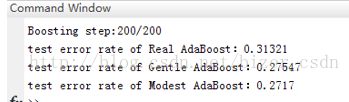
可见错误率并不理想,可能原因是LBP的灰度直方图特征是256维,并且AdaBoost内部用的弱分类器决策最大深度只是设置为4,非叶子节点最多15个,相比于256维很小,而增大深度,势必训练过程时间很长。
(2)PCA、LDA降维
而把人脸图像用PCA、LDA降维后只剩下一维特征,设置weak_learner= tree_node_w(1);然后训练AdaBoost分类器。load data\\train_data
train_num = size(tr_data,3);
%工具包要求类别标签设置为+1(男),-1(女);
tr_label(301:end)=-1;
%pca降维
row = 80;col = 80;
data1 = zeros(train_num,row*col);
for i=1:train_num
data1(i,:) = reshape(imresize(tr_data(:,:,i),[row,col]),[1,row*col]);
end
[coeff,score,latent] = pca(data1);
dim = 150;
while sum(latent(1:dim))/sum(latent) < 0.98
dim = dim + 1;
end
train_feature = score(:,1:dim);
w = Lda(train_feature',tr_label);
train_feature = (w'*train_feature')';
load data\\val_data
val_num = size(val_data,3);
%工具包要求类别标签设置为+1(男),-1(女);
val_label(81:end)=-1;
data2 = zeros(val_num,row*col);
for i=1:val_num
data2(i,:) = reshape(imresize(val_data(:,:,i),[row,col]),[1,row*col]);
end
val_score = bsxfun(@minus,data2,mean(data1,1))*coeff;
val_feature = val_score(:,1:dim);
val_feature = (w'*val_feature')';
load data\\test_data
test_num = size(te_data,3);
%工具包要求类别标签设置为+1(男),-1(女);
te_label(210:end)=-1;
data3 = zeros(test_num,row*col);
for i=1:test_num
data3(i,:) = reshape(imresize(te_data(:,:,i),[row,col]),[1,row*col]);
end
test_score = bsxfun(@minus,data3,mean(data1,1))*coeff;
test_feature = test_score(:,1:dim);
test_feature = (w'*test_feature')';
%通过训练集和验证集测试确定模型
MaxIter = 200; % boosting iterations
% and initializing matrices for storing step error
RAB_control_error = zeros(1, MaxIter);
MAB_control_error = zeros(1, MaxIter);
GAB_control_error = zeros(1, MaxIter);
验证集错误率随迭代过程如下:
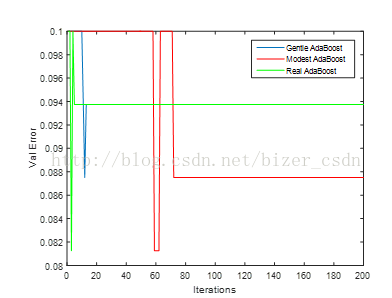
然后对测试集测试:

效果明显优于用LBP提取的直方图,但随着迭代过程,验证集上错误率出现跳变,并且三种AdaBoost方法在测试集结果一样,原因有待研究。
另外,相比于SVM方法,AdaBoost精度与其相差无几,可见PCA、LDA降维后提取的特征可以较好反应性别。
三、LBP\Fisherface+KNN
(1)LBP+KNN
助教提供的LBP用于性别识别的算法中,提取的LBP特征脸,并没有统计直方图,并把该特征通过PCA、LDA后,用SVM分类,正确率达到91.6891%。
另外,直接用LBP提取uniform模式下(uniform模式关注LBP算子从1到0或者从0到1的跳变,对于 阶灰度,模式种类可由 2^p减少到p*(p-1)+3 ,所以8阶灰度模式由256降低到59)的灰度直方图,得到59维特征,训练SVM,在测试集上的正确率只有77.3585%;如果,提取59维特征后,采用K-NN可方法匹配(K取奇数,采用1范数进行度量,对前K个匹配结果通过投票最终决定测试数据的性别), 正确率为66.79%,随着K增加正确率跟K关系如下:

效果并不理想,改为Fisher+KNN。
(2)Fisher准则函数
下图表示了在一个二维空间两个类别样本在两个不同的向量w1与w2上投影分布的情况。其中用红点及蓝点分别表示不同类别的样本。显然对向量W1的投影能使这两类有明显可分开的区域,而对向量W2的投影,则使两类数据部分交迭在一起,无法找到一个能将它们截然分开的界面。
Fisher准则的基本原理,就是要找到一个最合适的投影轴,使两类样本在该轴上投影的交迭部分最少,从而使分类效果为最佳。

(3)Fisherface方法
function [ train_lda,test_lda] = Fisherface(train,tr_label,test)
[nSmp,nFea] = size(train);
classLabel = unique(tr_label);%去除重复
nClass = length(classLabel);
%pca降维
if nFea > (nSmp - nClass)
[dataset_coef,train_score,dataset_latent,dataset_t2] = princomp(train);
test_score= bsxfun(@minus,test,mean(train,1))*dataset_coef;
train=train_score(:,1:nSmp-nClass);
test=test_score(:,1:nSmp-nClass);
[nSmp,nFea] = size(train);
end
sampleMean = mean(train);
Sb = zeros(nFea, nFea);
Sw = zeros(nFea, nFea);
for i = 1:nClass
index = find(tr_label==classLabel(i));
classMean = mean(train(index, :));
%类间散布矩阵
Sb = Sb + (length(index)/nSmp)*(sampleMean-classMean)'*(sampleMean-classMean);
%类内散布矩阵
Xclass=train(index,:);
tempSw=zeros(nFea,nFea);
for j=1:length(index)
tempSw=tempSw+(Xclass(j,:)-classMean)'*(Xclass(j,:)-classMean);
end
Sw=Sw + (length(index)/nSmp)*tempSw;
end
[eigvector, eigvalue] = eigs((Sw\Sb),nClass-1,'LR');
%投影
train_lda = train * eigvector;
test_lda = test * eigvector;
(4)knnRecognition
function [accurcy]=knnRecognition(train,train_label,test,test_label,kNum)
[rowTrain,colTrain]=size(train);
[rowTest,colTest]=size(test);
classLabel = unique(train_label);%去除重复
nClass = length(classLabel);
idx=knnsearch(test,train,kNum);
right=0;
for i=1 :rowTest
subIdx=idx(i,:);
classIdx=zeros(1,kNum);
for j=1 :kNum
temp=subIdx(j);
classIdx(j)=train_label(temp);
end
for k= 1: kNum
result=zeros(1,nClass);
classNum=classIdx(k);
dist=(norm(test(i,:)-train(subIdx(k),:)))^2;
result(classNum)=result(classNum)+1/dist;
dist=0;
end
[C,I]=max(result);
if(I==test_label(i))
right=right+1;
end
end
accurcy=right/rowTest;
(5)实验结果
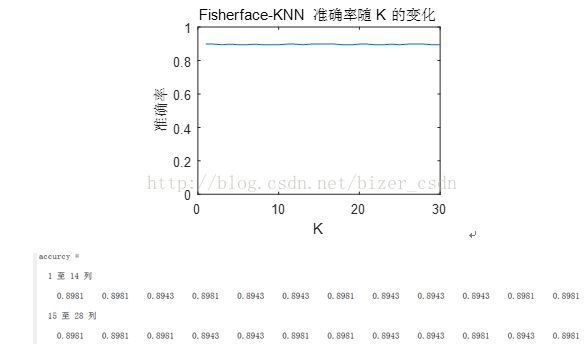
由实验结果可知,Fisherface+KNN可以达到近90%的准确率。且随着K值的变化,预测精度没有下降。
四、SIFT特征点
(1)SIFT+PCA+LDA+SVM
此外,助教还提供了基于SIFT的方法,对每张人脸图片提取SIFT关键点的128维特征,然后取其中前27个关键点,重排列成一个 维的向量,经过PCA、LDA后作为每张人脸图片的提取特征,仍然训练一个SVM对其进行分类。
%[image, descrips, locs] = sift('scene.pgm');
DatFile = sprintf('data\\Data1_SIFT.mat');
load data\train_data
load data\test_data
train_num = size(tr_data,3);
test_num = size(te_data,3);
row = 35;
col = 128;
data1 = zeros(train_num,row*col);
load data\\Data1_SIFT.mat
[coeff,score,latent] = princomp(data1);
dim = 150;
while sum(latent(1:dim))/sum(latent) < 0.98
dim = dim + 1;
end
feature = score(:,1:dim);
w = Lda(feature',tr_label);
feature = (w'*feature')';
model = svmtrain(tr_label',feature,'-s 0 -t 0');
DatFile2 = sprintf('data\\Data2_SIFT.mat');
data2 = zeros(test_num,row*col);
load data\\Data2_SIFT.mat
test_score = bsxfun(@minus,data2,mean(data1,1))*coeff;
test_feature = test_score(:,1:dim);
test_feature = (w'*test_feature')';
[p1,a1,d1] = svmpredict(te_label',test_feature,model);
最终结果:

效果并不理想,SIFT主要用于提取图片关键点,对于尺度变化不敏感,所以适合用于匹配的,而SIFT提取特征对性别不怎么敏感,这个原因可能导致结果并不理想。
(2)SIFT+随机森林
随机森林由许多的决策树组成,因为这些决策树的形成采用了随机的方法,所以叫做随机森林。随机森林中的决策树之间是没有关联的,当测试数据进入随机森林时,其实就是让每一颗决策树进行分类看看这个样本应该属于哪一类,最后取所有决策树中分类结果最多的那类为最终的结果(每棵树的权重要考虑进来)。所有的树训练都是使用同样的参数,但是训练集是不同的,分类器的错误估计采用的是oob(out of bag)的办法。因此随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定。
load('data\test_data.mat')
load('data\train_data.mat')
load('data\Data1_SIFT.mat')
load('data\Data2_SIFT.mat')
dataTrain=double(data1);
dataTest=double(data2);
trainLabel=tr_label';
testLabel=te_label';
rng(1);
BaggedEnsemble2 = TreeBagger(2,dataTrain,trainLabel,'OOBPrediction','On',...
'Method','classification')
[Predict_label,Scores] = predict(BaggedEnsemble2, dataTest);
p_label=double(cell2mat(Predict_label));
p_label=p_label-48;
accuracy=( testLabel== p_label);
error_rate=1-sum(accuracy)/256
BaggedEnsemble = TreeBagger(1200,dataTrain,trainLabel,'OOBPrediction','On',...
'Method','classification')
view(BaggedEnsemble.Trees{1},'Mode','graph')
oobErrorBaggedEnsemble = oobError(BaggedEnsemble);
plot(oobErrorBaggedEnsemble)
xlabel('树的数量')
ylabel('错误率')
title('随机森林')
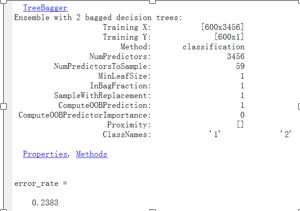
下图为错误率随着随机树的数量增长的变化趋势图:

决策树的结构:
五、总结:
本次作业共采用了5种方法,其对应实验结果如下:
| vgg+PCA+LDA+SVM |
AdaBoost+LBP+LDA |
Fisherface+KNN |
SIFT特征点+PCA+SVM |
SIFT特征点+随机森林 |
| 91.70% |
94.80% |
89.80% |
69.1% |
76.30% |
代码已上传

