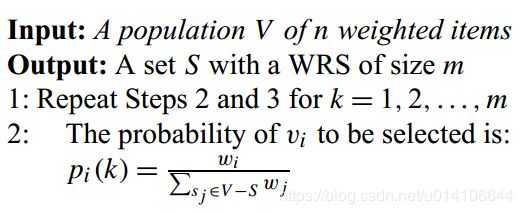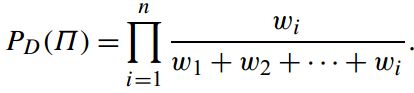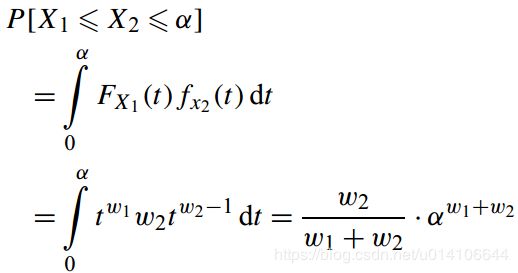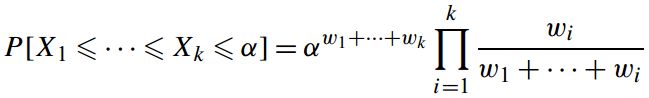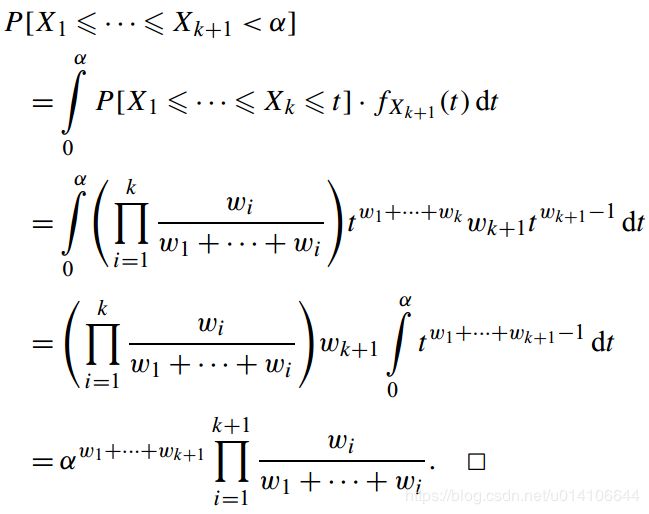机器学习--蓄水池抽样与加权抽样算法

学习一下蓄水池抽样以及加权抽样算法

1.蓄水池抽样

如果数据总量是有限的，随机抽样k个值，可以直接利用随机数产生器来产生。如果数量总量是不断增加的，内存并不能完全存放所有数据，此时若随机产生k个值可以采用蓄水池抽样算法。

1.从一个数据流中随机取出一个数，要求每个数被取到的概率相等

第一个数以概率1取值，第二个数以1/2概率替换，第三个数以1/3概率替换。。。。直到第n个数

第一个数被取到的概率  第一个数取到并且后面没有被替换掉

1*1/2*2/3*3/4.......(n-1)/n=1/n

第k个数，最后被取到的概率    第k个数被取到，并且后面没有被替换掉

1/k * k/k+1 * k+1/k+2 *.... n-1/n = 1/n

即每个数被取到的概率是相等的

python编程实现：

def random(num=[]):
    import numpy as np
    i = 2
    r = num[1]
    while i

randint(a,b)可以产生一个[a,b]的随机数，下式成立的概率应该为1/i

np.random.randint(1, i)==i

后来测试发现randint(a,b)不会产生等于b的随机数，修改右端点为i+1 这样np.random.randint(1, i+1)即可产生1--i的随机数，等于1的概率即为1/i

def random(num=[]):
    import numpy as np
    i = 2
    r = num[1]
    while i

后来查了一下，发现自己搞错了，randint(a,b)可以产生一个[a,b)的随机数,右边界取不到

2.从一个数据流中随机选取k个数，要求每个被选取到的概率相等

蓄水池采样算法：

先将k个数放入到蓄水池中，后面的每一个数(>k)都已k/k+1的概率换入蓄水池，换入时随机选取蓄水池的一个数换出

第一个数被选中的概率是   第一个数被选中*（后面的数没有被选中+后面的数被选中但是没有替换掉1）

1 * （1/k+1 * k-1/k + k/k+1）*(1/k+2 * k-1/k + k+1/k+2) *......  *(1/n*k-1/k +n-1/n)=  k/n;

对于数据流不断增加，数据中某个值，被选中的概率是：

当数据小于肯定不会选中，因为数据中没有该值；

当数据流等于时其被选中的概率为k/;

当数据流大于时，要保证后面的每个数不会替换掉。

代码如下：

def randomk(k, num=[]):
    import numpy as np
	#坐标索引不会取到右端点
    r = num[1:k+1]
    i = k+1
    while i

j = np.random.randint(1, i+1) 产生[1,i]的随机数  j<=k的概率为k/i,以该概率将蓄水池中j位置换为num[i]元素即可。

以上实现了蓄水池抽样，特别是数据源不确定时，下面是加权抽样，即每个数据点都有一个权重，可以简单分为数据源有限以及无限的情况。

2.加权抽样

参考论文《Weighted random sampling with a reservoir》以及链接：https://blog.csdn.net/xiao2cai3niao/article/details/80587471

算法1：数据集有限：

wn被选中的概率为：wn/(w1 + w2 + ··· + wn)  wn-1被选中的概率为：wn-1/(w1 + w2 + ··· + wn-1)

每一个标签依次选中的可能性为：

算法2：数据集有限

给定数据以及相应权重，利用权重以及随机数来给每一个数据打分

最终挑选出分值最大的k个数作为最终结果返回。

算法3： 数据集有限

利用指数分布：

为每一个标签生成一个指数分布为标签权重，然后每个分布随机产生一个数值，挑选随机数值最大的k个标签返回即可。

算法4：数据集无限

当数据集无限时，不能采用算法1来计算所有标签的分值，可以采用蓄水池抽样算法来实现。

为每一个样本生成一个分数： 

如果不足 k 个，直接保存

如果已经有 k 个，如果 ki 比已有的结果里最小那个分数大，就替换

 

下面依次给出算法1和2的正确性

然后给出算法4的正确性

算法2和算法1等效性的证明：

Ui为(0,1)之间随机数  wi为数据i的权重，Xi为数据i的分数  为[0,1]之间的一个实数，现在证明以上命题。

定义分布函数：

概率密度函数为：

n=1时有：

n=2时有：

假设n=k时成立：

当n=k+1时：

 

参考文献：

https://blog.csdn.net/xiao2cai3niao/article/details/80587471

https://blog.csdn.net/zm714981790/article/details/51407552

https://blog.csdn.net/chouisbo/article/details/55046128

https://www.jianshu.com/p/63f6cf19923d

大神论文：《Weighted random sampling with a reservoir》